系列文章目录
路径规划之Dijkstra算法
路径规划之Best-First Search算法
路径规划之A*算法
路径规划之A*算法
- 系列文章目录
- 前言
- 一、前期准备
- 1.1 算法对比
- 1.2 数学式方法
- 1.3 启发式方法
- 二、A*算法
- 2.1 起源
- 2.2 思想
- 2.3 启发式函数
- 2.4 过程
- 2.5 案例查看
前言
之前提过Dijkstra算法的核心是每次遍历寻找离起点代价最小的点作为新的节点,Best-First Search算法的核心是每次遍历寻找离终点代价最小的点作为节点;二者各有优缺,所以就有大佬将二者结合起来提出了A*算法。
一、前期准备
1.1 算法对比
| 算法 | 思想 | 优点 | 缺点 |
|---|---|---|---|
| Dijkstra | 寻找离起点代价最小的点 | 确保能找到最短路径 | 运行时间长 |
| Best-First Search | 寻找离终点代价最小的点 | 运行时间短 | 地图存在障碍物时难以找到最短路径 |
1.2 数学式方法
在寻找路径的问题中,数学式方法通常通过处理抽象图的属性,以及规定和分析有序检查图的节点以建立
最小成本路径的算法。
代表算法就是Dijsktra算法。然而,数学式方法通常更关注解决方案的最终实现,却很少考虑算法的时间复杂度。
1.3 启发式方法
启发式方法指人在解决问题时所采取的一种根据经验规则进行发现的方法。其特点是在解决问题时,利用
过去的经验,选择已经行之有效的方法,而不是系统地、以确定的步骤去寻求答案。
博主刚看这个概念的时候脑子一闪而过动态规划的定义,而在寻找路径的问题中,使用关于由图表示的问题的领域的特殊知识,启发式方法通常可以提高特定图搜索问题的解决方案的计算效率。 然而,启发式方法通常无法保证始终找到最低权值(cost)的解决方案路径,Best-First Search就属于启发式方法。
二、A*算法
2.1 起源
A*算法于1968年由计算机科学家Peter Hart、Nils Nilsson和Bertram Raphael提出,它将Dijkstra和Best-First Search二者的优点结合起来,兼顾了 Dijkstra 的准确度和 Best-First Search的效率,可以快速有效地寻找到图中的最短路径,是应用最广的寻路算法。
2.2 思想
类似于Dijkstra和Best-First Search,它们的算法核心在1.1中已经提到了,而建立在二者之上的A算法的核心如下
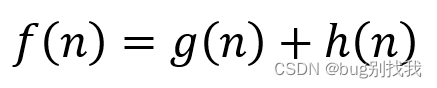
f(n)代表A的代价函数,g(n)代表当前点距离起点的代价,h(n)代表当前点距离终点的代价
2.3 启发式函数
在上述的代价函数中,我们知道f(n)是g(n)和h(n)两部分组成,g(n)是一个已知代价函数,而h(n)作为一个启发式函数,它的选择至关重要。
开始的时候博主不知道为什么h(n)是一个启发式函数,不是只要直接计算终点到当前点的距离就行了吗?

但是在实际应用中,不是单纯地计算距离就行的,当前点距离终点的路径上会存在很多路障,只要存在一个路障,单纯地计算距离这种方法直接gg;因此,选择一个好的启发式函数是重要的,它可以有效评估最小代价。以下是不同启发式函数的效果。
| 取值 | 过程 | 结果 |
|---|---|---|
| h(n)=0 | 演变成Dijkstra算法 | 保证找到最短路径 |
| h(n)>>g(n) | 演变成BFS算法 | 不保证找到最短路径,但运算快 |
| h(n)<实际代价 | h(n)越小,A*扩展结点越多,运行越慢 | 保证找到最短路径,运算相对Dijkstra快一些 |
| h(n)=实际代价 | 仅仅寻找最佳路径而不扩展别的任何结点 | 保证找到最短路径,运算非常快 |
| h(n)>实际代价 | 寻找最佳路径且扩展别的任何结点 | 不保证找到最短路径,但运算快 |
2.4 过程
-
将起点放入到“开放列表”(open list)中,
-
重复如下过程:
① 遍历开放列表,计算列表中每一个节点的评价函数。查找 值最小的节点,把它作为当前要处理的节点。
② 对当前节点中,与之相邻的其他所有节点,做如下操作:
若节点是不可抵达的(unreachable),或者在关闭列表(closed list)中,忽略它。否则,做如下操作。
若节点不在开放列表中,则将其加入开放列表,并将当前节点设置为其父亲节点,计算节点的和。
若节点已经在开放列表中,则需要检查这条路径(节点到节点的路径)是否更好。参考指标为值,若更小,则说明该路径更好。若这条路径更好,则将它的父亲节点(设为节点)设置为当前节点,并重新计算和。
③ 将n移动到“关闭列表”(closed list)中。关闭列表中的所有元素已经不需要被关注。 -
当满足如下条件中的一个时,程序终止。
将终点加入到了开放列表中(此时路径已经找到了)。
无法查找到终点,并且此时开放列表是空列表(此时没有路径)。 -
若终点已经找到,查找最短路径:从终点开始,每个节点都沿着父亲节点移动,直到起点。
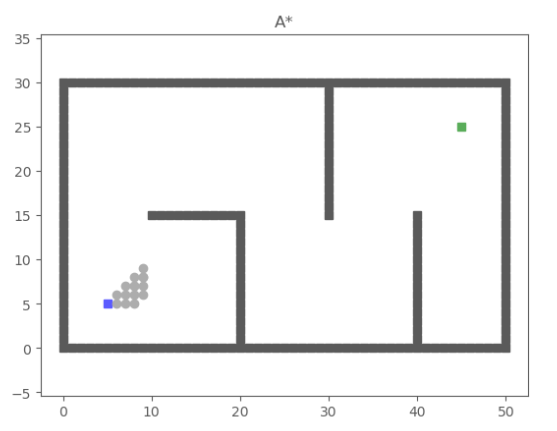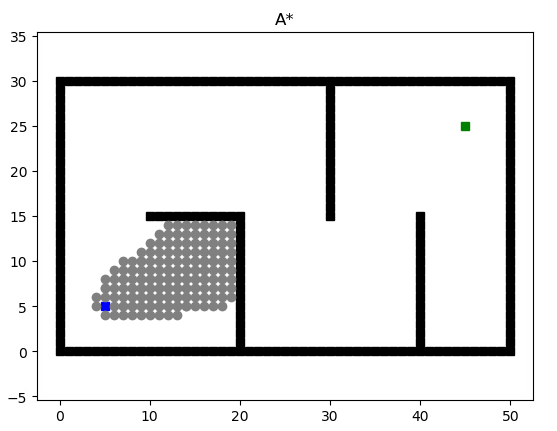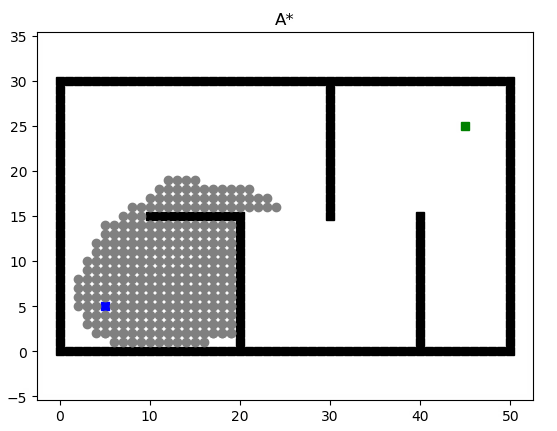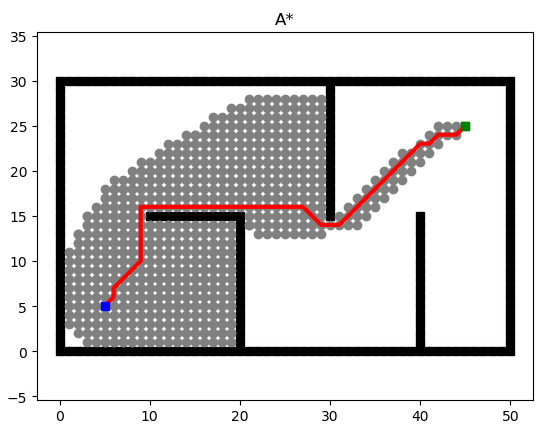
2.5 案例查看
下图是A*算法在一个简单地图中的应用