这篇文章我们来一起学习一个算法——快速幂算法。

1. 什么是快速幂

顾名思义，快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高。

那快速幂算法呢一般就是用来解决如下的问题：

我们看到它的取值范围是比较大的，所以我们可以用long long

2. 暴力求解

代码实现

那这个问题呢乍一看很简单：

我们可以考虑用循环（或者使用pow函数）直接计算a^b的值，然后对c去模即可。

缺陷分析

但是呢，这样写我们的算法其实是有去缺陷的：

首先它的时间复杂度是O(b)，而上面题目中b的取值是【0，10^18】。
所以当b的取值比较大的时候，时间复杂度就会很大，那么算法的效率就比较低。
此外这里的ret不断乘等以a，它的范围是很有可能超过long long 的。

那一旦溢出的话，结果可能就错了。

所以我们要想办法对该算法进行优化

3. 优化一：取模运算的性质

首先我们可以根据取模运算的性质进行第一重优化：

取模运算是满足这样一条性质的
(a*b)%c=((a%c)*(b%c))%c
大家有兴趣可以自己证明一下
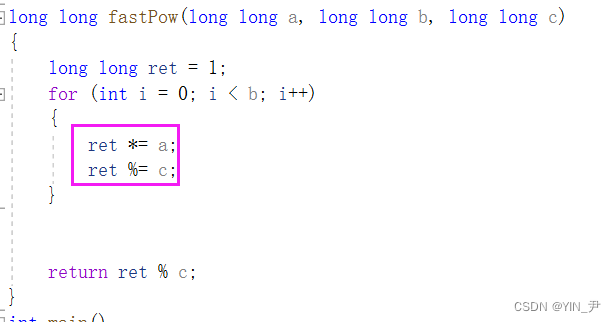
那这样的话我们之前是每次让ret*=a，乘等b次，最后再去模。
那现在我们可以在每次ret*=a之后都对ret进行一次取模

那这样的话ret就不太容易溢出了。

long long fastPow(long long a, long long b, long long c)
{
	long long ret = 1;
	for (int i = 0; i < b; i++)
	{
		ret *= a;
		ret %= c;
	}

	return ret % c;
}

但是，是否仍然有缺陷呢？

🆗，它的时间复杂度并没有得到优化，还是O(b)

所以，我们再来想办法优化：

4. 优化二：快速幂算法的核心思想

快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。

我们来举个例子：

比如算3^10
那其实可以这样写：
3^10=(3^2)^5=9^5=9*9^4=9*81^2
那观察这个式子其实我们能发现这样的规律：

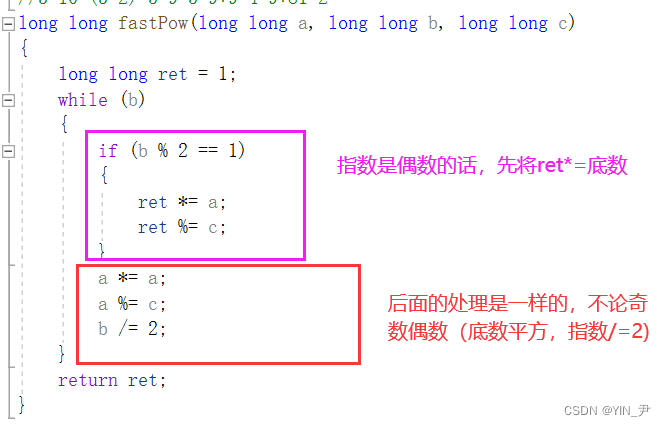
1. 如果指数是是偶数的话，那么指数除以2，底数平方，前后的值是相等的。（ret*3^10=ret*(3^2)^5）
2. 如果指数是奇数的话，先将ret*=底数，然后依然是指数除以2，底数平方，前后值相同（ret*9^5=ret*9*81^2）

那我们来算一下这种写法的时间复杂度：

这样优化之后呢，每次指数的值都会/=2，即b/=2，那之前我们要循环b次，现在就是O(logb)，即以2为底，b的对数。

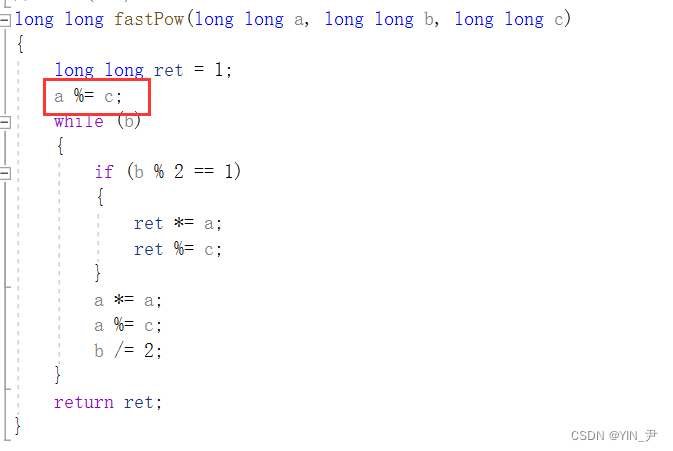
那我们来写一下代码：

那此外，为了防止输入的a过大的话，我们上来可以直接对a取模

5. 终极优化：位运算优化

那针对上面的代码，有两处地方我们其实还可以进行一个优化：

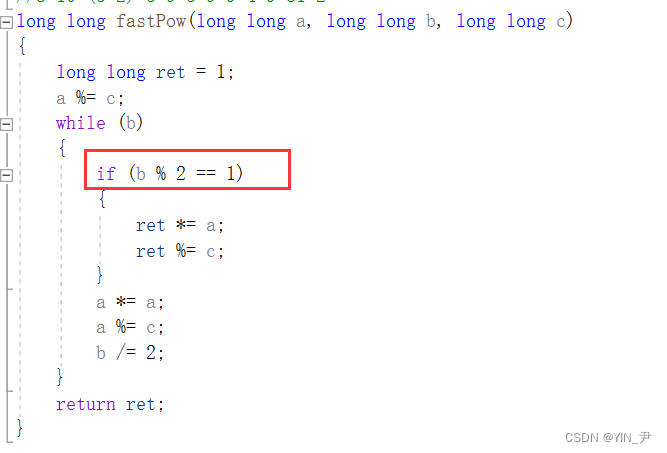
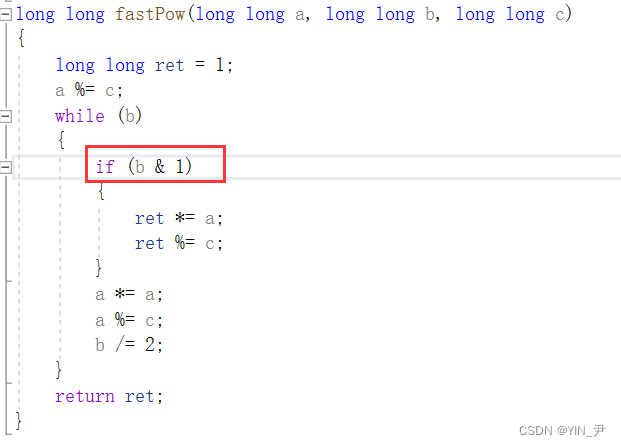
首先

判断指数是偶数还是奇数这里，还有一种更高效的方法就是使用位运算，让b&1，因为1的补码只有最后一位为1，其余全为0，如果b是奇数的话，那它的最后一位为1，b&1的结果就是1，如果b是偶数，那最后一位为0，b&1的结果是0

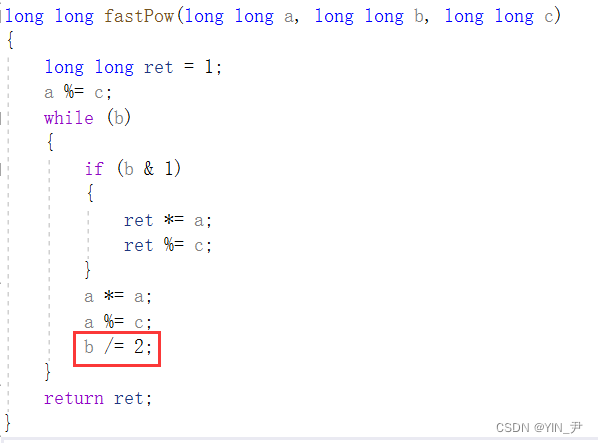
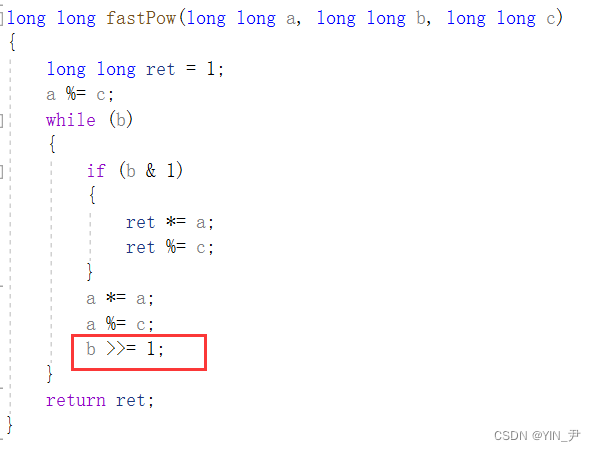
然后就是：

b/=2这里，我们可以用b>>=1代替（整数算术右移一位相当于除以2并向下取整）

关于移位操作符如果大家遗忘了可以看： 【C操作符详解】之 移位操作符

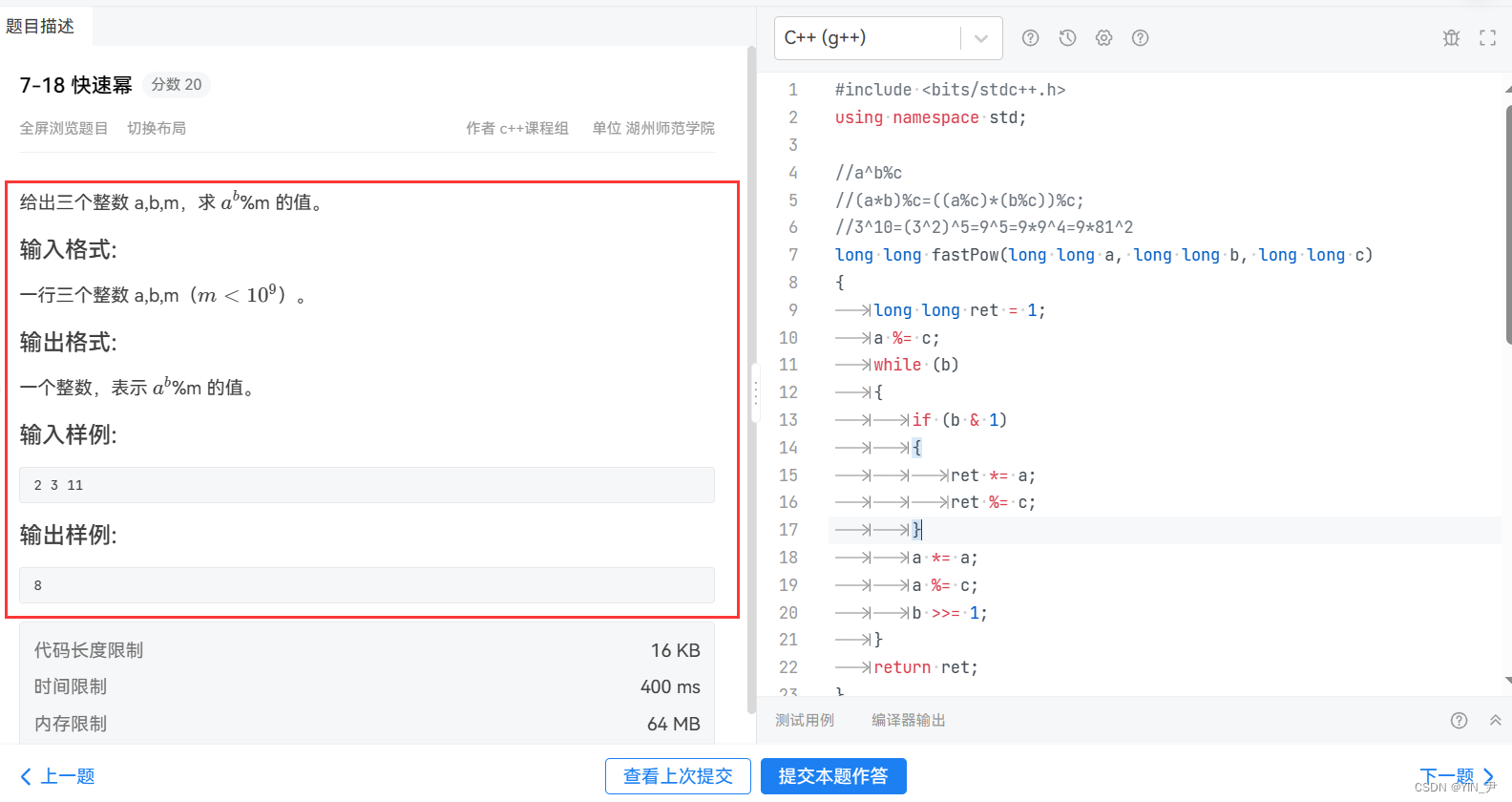
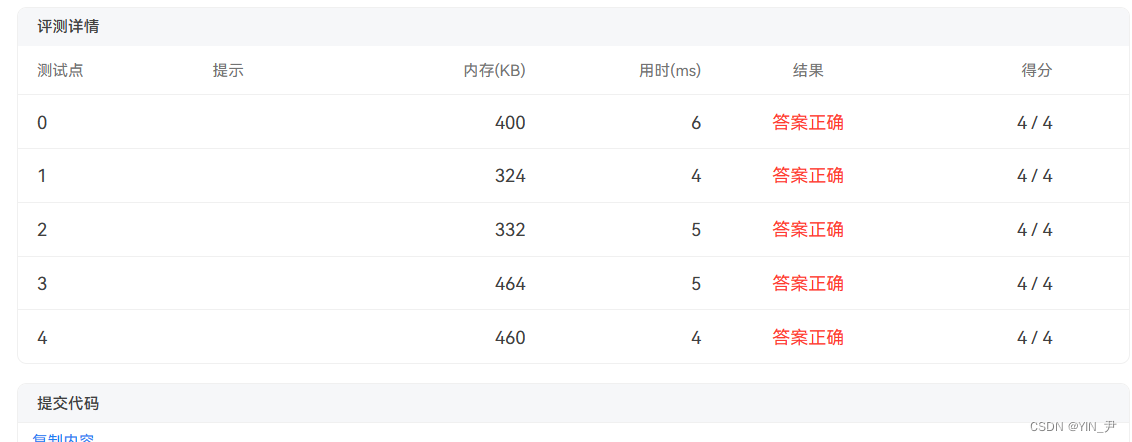
我找了一道OJ，我们可以来测试一下：

没有问题！

6. 源码

#include <iostream>
using namespace std;
long long fastPow(long long a, long long b, long long c)
{
	long long ret = 1;
	a %= c;
	while (b)
	{
		if (b & 1)
		{
			ret *= a;
			ret %= c;
		}
		a *= a;
		a %= c;
		b >>= 1;
	}
	return ret;
}

int main()
{
	long long a = 0;
	long long b = 0;
	long long m = 0;
	cin >> a >> b >> m;
	cout << fastPow(a, b, m) << endl;
	return 0;
}