算法竞赛备赛进阶之状态压缩训练

状态压缩

状态压缩DP是一种暴力的算法，它需要遍历每个状态，而每个状态是多个事件的集合。这种算法通常用于小规模问题的求解，因为它的复杂度是指数级别的。

状态压缩DP的两个基本特征包括问题的数据规模特别小，可以通过2的阶乘次进行求解，且题目通常都是选与不选两种选择，可以使用二进制串表示。

状态压缩DP通常使用二进制数来表示状态。一个数就能表示一个状态，通常一个状态数据就是一个一串0和1组成的二进制数，每一位二进制数只有两种状态，比如说硬币的正反两面，10枚硬币的结果就可以用10位二进制数完全表示出来，每一个10位二进制数就表示了其中一种结果。使用二进制数表示状态不仅缩小了数据存储空间，还能利用二进制数的位运算很方便地进行状态转移。

状态压缩DP：

状态表示f[i, j, s]
1. 集合：所有只摆在前i行，已经摆了j个数据，并且在第i行摆放的状态是s的所有方案的集合
2. 属性：Count
状态计算

已经摆完前i排，并且第i排的状态a，第i-1排的状态是b，已经摆了j个物品的所有方案。

已经摆完前i-1排，并且第i-1排的状态是b，已经摆了j-count(a)个物品的所有方案，f[i-1, j-count(a), b]

第i-1行内部不能有两个1相邻
第i-1行和第i行之间也不能相互攻击到
(a & b) == 0 (a | b)不能有两个相邻的1
状态数量*状态转移的计算量

1.小国王

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。输入格式共一行，包含两个整数 n 和 k。输出格式共一行，表示方案总数，若不能够放置则输出0。数据范围 1≤n≤10, 0≤k≤n2

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>

using namespace std;

const int N = 12, M = 1 << 10, k = 110;

typedef long long LL;

int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
LL f[N][K][M];

bool check(int state)
{
    for(int i = 0;i < n; i++)
        if((state >> i & 1) && (state >> i + & 1))
            return false;
    return true;
}

int count(int state)
{
    int res = 0;
    for(int i = 0;i < n; i++) res += state >> i & 1;
    return res;
}

int main()
{
    cin >> n >> m;
    
    for(int i = 0;i < n; i++)
        if(check(i))
        {
            state.push_back(i);
            cnt[i] = count(i);
        }
    
    for(int i = 0;i < state.size(); i++)
        for(int j = 0;j < state.size(); j++)
        {
            int a = state[i], b = state[j];
            if((a % b) == 0 && check(a | b))
                head[a].push_back(b);
        }
    
    f[0][0][0] = 1;
    for(int i = 1;i <= n + 1; i++)
        for(int j = 0;j <= m; j++)
            for(int a = 0;a < state.size(); a++)
                for(int b : head[a])
                {
                    int c = cnr[state[a]];
                    if(j >= c)
                        f[i][j][a] += f[i - 1][j - c][b];
                }
    
    cout << f[n + 1][m][0] << endl;
    
    return 0;
}

2.玉米田

农夫约翰的土地由 M×N 个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式

第 1 行包含两个整数 M 和 N。

第 2..M+1 行：每行包含 N 个整数 0 或 1，用来描述整个土地的状况，1 表示该块土地肥沃，0 表示该块土地不育。

#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 14, M = 1 << 12, mod = 1e8;

int n, m;
int g[N];
vector <int> state;
vector <int> head[M];
int f[N][M];

bool check(int state)
{
    for(int i = 0;i < m; i++)
        if((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 1;i <= n; i++)
        for(int j = 0;j < m; j++)
        {
            int t;
            cin >> t;
            g[i] += |t << j;
        }
    
    for(int i = 0;i < 1 << m; i++)
        if(check(i))
            state.push_back(i);
    
    for(int i = 0;i < state.size(); i++)
        for(int j = 0;j < state.size(); j++)
        {
            int a = state[i], b = state[j];
            if((a & b) == 0)
                head[i].push_back(j);
        }
    
    f[0][0] = 1;
    for(int i = 1;i <= n + 1; i++)
        for(int a = 0;a < state.size(); a++)
            for(int b : head[a])
            {
                if(g[i] & state[a]) continue;
                f[i][a] = (f[i][a] + f[i - 1][b]) % mod;
            }
    
    printf("%d\n", f[n + 1][0]);
    return 0;
}

3.炮兵阵地

司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。

一个 N×M 的地图由 N 行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

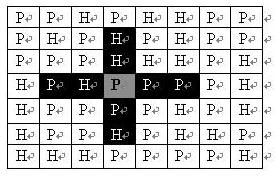
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 N 和 M；

接下来的 N 行，每一行含有连续的 M 个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

已经摆完前i行，且第i行的状态是a，第i-1行的状态是b的所有摆放方案。

已经摆完前i-1行，且第i-1行的状态是b的所有摆放方案。f[i-1, b]

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 11, M = 1 << 10;

int n, m;
int g[110];
vector<int> state;
int f[2][M][M];
int cnt[M];

bool check(int state)
{
    for(int i = 0;i < m; i++)
        if((state >> i & 1) && ((state >> i + 1 & 1) | (state >> i + 2 & 1)))
            return false;
    return true;
}

int count(int state)
{
    int res = 0;
    for(int i = 0;i < m; i++) res += state >> i & 1;
    return res;
}

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i++)
        for(int j = 0;j < m; j++)
        {
            char c;
            cin >> c;
            if(c == 'H') g[i] += 1 << j;
        }
    
    for(int i = 0;i < 1 << m; i++)
        if(check(i))
        {
            state.push_back(i);
            cnt[i] = count(i);
        }
    
    for(int i = 1; i<= n + 2; i++)
        for(int j = 0;j < state.size(); j++)
            for(int k = 0;k < state.size(); k++)
                for(int u = 0;u < state.size(); u++)
                {
                    int a = state[j], b = state[k], c = state[u];
                    if((a & b) | (b & c) | (a & c)) continue;
                    if(g[i - 1] & a | g[i] & b) continue;
                    f[i & 1][j][k] = max(f[i & 1][j][k], f[i - 1 & 1][u][j] + cnt[b]);
                }
    
    cout << f[n + 2 & 1][0][0] << endl;
    
    return 0;
}

4.愤怒的小鸟

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0)(0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax2+bxy=ax2+bx 的曲线，其中 a,ba,b 是 Kiana 指定的参数，且必须满足 a<0a<0。

当小鸟落回地面（即 xx 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 nn 只绿色的小猪，其中第 ii 只小猪所在的坐标为 (xi,yi)(xi,yi)。

如果某只小鸟的飞行轨迹经过了 (xi, yi)(xi, yi)，那么第 ii 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 (xi, yi)(xi, yi)，那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3)(1,3) 和 (3,3)(3,3)，Kiana 可以选择发射一只飞行轨迹为 y=−x2+4xy=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana 来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个这个游戏。

这些指令将在输入格式中详述。

假设这款游戏一共有 TT 个关卡，现在 Kiana 想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。

由于她不会算，所以希望由你告诉她。

注意:本题除 NOIP 原数据外，还包含加强数据。

输入格式

第一行包含一个正整数 T，表示游戏的关卡总数。

下面依次输入这 T 个关卡的信息。

每个关卡第一行包含两个非负整数 n,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。

接下来的 nn 行中，第 ii 行包含两个正实数 (xi,yi)，表示第 ii 只小猪坐标为 (xi,yi)，数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0，表示 Kiana 输入了一个没有任何作用的指令。

如果 m=1，则这个关卡将会满足：至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。

如果 m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 ⌊n/3⌋只小猪。

保证 1≤n≤18，0≤m≤2，0<xi,yi<10，输入中的实数均保留到小数点后两位。

上文中，符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整，例如：⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;

const int N = 18, M = 1 << 18;
const double eps = 1e-8;

int n, m;
PDD q[N];
int path[N][N];
int f[M];

int cmp(double x, double y)
{
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

int main()
{
    int T;
    cin >> T;
    while (T -- )
    {
        cin >> n >> m;
        for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;

        memset(path, 0, sizeof path);
        for (int i = 0; i < n; i ++ )
        {
            path[i][i] = 1 << i;
            for (int j = 0; j < n; j ++ )
            {
                double x1 = q[i].x, y1 = q[i].y;
                double x2 = q[j].x, y2 = q[j].y;
                if (!cmp(x1, x2)) continue;
                double a = (y1 / x1 - y2 / x2) / (x1 - x2);
                double b = y1 / x1 - a * x1;

                if (cmp(a, 0) >= 0) continue;
                int state = 0;
                for (int k = 0; k < n; k ++ )
                {
                    double x = q[k].x, y = q[k].y;
                    if (!cmp(a * x * x + b * x, y)) state += 1 << k;
                }
                path[i][j] = state;
            }
        }

        memset(f, 0x3f, sizeof f);
        f[0] = 0;
        for (int i = 0; i + 1 < 1 << n; i ++ )
        {
            int x = 0;
            for (int j = 0; j < n; j ++ )
                if (!(i >> j & 1))
                {
                    x = j;
                    break;
                }

            for (int j = 0; j < n; j ++ )
                f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);
        }

        cout << f[(1 << n) - 1] << endl;
    }

    return 0;
}