04 概率论基础
- 概率论公理
- 联合概率
- 条件概率
- 贝叶斯定理
- 边际化
- 独立性
- 期望和方差
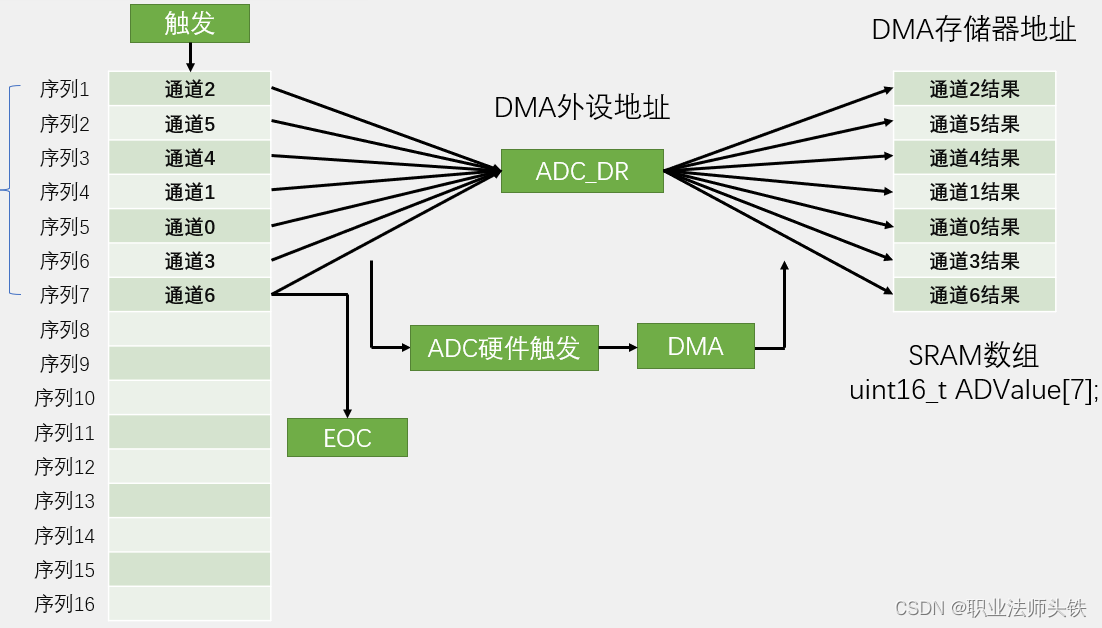
- 模拟投掷骰子的概率随投掷次数增加的变化
概率论公理
概率(probability)可以被认为是将集合映射到真实值的函数。
在给定的样本空间
S
\mathcal{S}
S中,事件
A
\mathcal{A}
A的概率,
表示为
P
(
A
)
P(\mathcal{A})
P(A),满足以下属性:
- 对于任意事件 A \mathcal{A} A,其概率从不会是负数,即 P ( A ) ≥ 0 P(\mathcal{A}) \geq 0 P(A)≥0;
- 整个样本空间的概率为 1 1 1,即 P ( S ) = 1 P(\mathcal{S}) = 1 P(S)=1;
- 对于互斥(mutually exclusive)事件(对于所有 i ≠ j i \neq j i=j都有 A i ∩ A j = ∅ \mathcal{A}_i \cap \mathcal{A}_j = \emptyset Ai∩Aj=∅)的任意一个可数序列 A 1 , A 2 , … \mathcal{A}_1, \mathcal{A}_2, \ldots A1,A2,…,序列中任意一个事件发生的概率等于它们各自发生的概率之和,即 P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty} \mathcal{A}_i) = \sum_{i=1}^{\infty} P(\mathcal{A}_i) P(⋃i=1∞Ai)=∑i=1∞P(Ai)。
联合概率
P ( A = a , B = b ) P(A=a,B=b) P(A=a,B=b)
给定任意值 a a a和 b b b,联合概率可以回答: A = a A=a A=a和 B = b B=b B=b同时满足的概率是多少?
对于任何 a a a和 b b b的取值, P ( A = a , B = b ) ≤ P ( A = a ) P(A = a, B=b) \leq P(A=a) P(A=a,B=b)≤P(A=a)。
条件概率
0
≤
P
(
A
=
a
,
B
=
b
)
P
(
A
=
a
)
≤
1
0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1
0≤P(A=a)P(A=a,B=b)≤1。
我们称这个比率为条件概率(conditional probability),
并用
P
(
B
=
b
∣
A
=
a
)
P(B=b \mid A=a)
P(B=b∣A=a)表示它:它是
B
=
b
B=b
B=b的概率,前提是
A
=
a
A=a
A=a已发生。
贝叶斯定理
根据乘法法则(multiplication rule )可得到
P
(
A
,
B
)
=
P
(
B
∣
A
)
P
(
A
)
P(A, B) = P(B \mid A) P(A)
P(A,B)=P(B∣A)P(A)。
根据对称性,可得到
P
(
A
,
B
)
=
P
(
A
∣
B
)
P
(
B
)
P(A, B) = P(A \mid B) P(B)
P(A,B)=P(A∣B)P(B)。
假设
P
(
B
)
>
0
P(B)>0
P(B)>0,求解其中一个条件变量,我们得到
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) . P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}. P(A∣B)=P(B)P(B∣A)P(A).
其中
P
(
A
,
B
)
P(A, B)
P(A,B)是一个联合分布(joint distribution),
P
(
A
∣
B
)
P(A \mid B)
P(A∣B)是一个条件分布(conditional distribution)。
这种分布可以在给定值
A
=
a
,
B
=
b
A = a, B=b
A=a,B=b上进行求值。
边际化
为了能进行事件概率求和,需要求和法则(sum rule),
即
B
B
B的概率相当于计算
A
A
A的所有可能选择,并将所有选择的联合概率聚合在一起:
P ( B ) = ∑ A P ( A , B ) , P(B) = \sum_{A} P(A, B), P(B)=A∑P(A,B),
这也称为边际化(marginalization)。
边际化结果的概率或分布称为边际概率(marginal probability)
或边际分布(marginal distribution)。
独立性
如果两个随机变量
A
A
A和
B
B
B是独立的,意味着事件
A
A
A的发生跟
B
B
B事件的发生无关。
在这种情况下,通常将这一点表述为
A
⊥
B
A \perp B
A⊥B。
根据贝叶斯定理,马上就能同样得到
P
(
A
∣
B
)
=
P
(
A
)
P(A \mid B) = P(A)
P(A∣B)=P(A)。
在所有其他情况下,我们称
A
A
A和
B
B
B依赖。
由于
P
(
A
∣
B
)
=
P
(
A
,
B
)
P
(
B
)
=
P
(
A
)
P(A \mid B) = \frac{P(A, B)}{P(B)} = P(A)
P(A∣B)=P(B)P(A,B)=P(A)等价于
P
(
A
,
B
)
=
P
(
A
)
P
(
B
)
P(A, B) = P(A)P(B)
P(A,B)=P(A)P(B),
因此两个随机变量是独立的,当且仅当两个随机变量的联合分布是其各自分布的乘积。
同样地,给定另一个随机变量
C
C
C时,两个随机变量
A
A
A和
B
B
B是条件独立的(conditionally independent),
当且仅当
P
(
A
,
B
∣
C
)
=
P
(
A
∣
C
)
P
(
B
∣
C
)
P(A, B \mid C) = P(A \mid C)P(B \mid C)
P(A,B∣C)=P(A∣C)P(B∣C)。
这个情况表示为
A
⊥
B
∣
C
A \perp B \mid C
A⊥B∣C。
期望和方差
一个随机变量 X X X的期望(expectation,或平均值(average))表示为
E [ X ] = ∑ x x P ( X = x ) . E[X] = \sum_{x} x P(X = x). E[X]=x∑xP(X=x).
当函数 f ( x ) f(x) f(x)的输入是从分布 P P P中抽取的随机变量时, f ( x ) f(x) f(x)的期望值为
E x ∼ P [ f ( x ) ] = ∑ x f ( x ) P ( x ) . E_{x \sim P}[f(x)] = \sum_x f(x) P(x). Ex∼P[f(x)]=x∑f(x)P(x).
在许多情况下,我们希望衡量随机变量 X X X与其期望值的偏置。这可以通过方差来量化
V a r [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − E [ X ] 2 . \mathrm{Var}[X] = E\left[(X - E[X])^2\right] = E[X^2] - E[X]^2. Var[X]=E[(X−E[X])2]=E[X2]−E[X]2.
方差的平方根被称为标准差(standard deviation)。
随机变量函数的方差衡量的是:当从该随机变量分布中采样不同值
x
x
x时,
函数值偏离该函数的期望的程度:
V a r [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] . \mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right]. Var[f(x)]=E[(f(x)−E[f(x)])2].
模拟投掷骰子的概率随投掷次数增加的变化
%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l
为了抽取像本,即掷骰子,我们只需为了抽取一个样本,
输出是另一个相同长度的向量:它在索引
i
i
i处的值是采样结果中
i
i
i出现的次数。
fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()
tensor([0., 1., 0., 0., 0., 0.])
使用PyTorch框架的函数同时抽取多个样本,得到我们想要的任意形状的独立样本数组
multinomial.Multinomial(10, fair_probs).sample()
tensor([3., 2., 0., 3., 1., 1.])
模拟1000次投掷,
然后统计1000次投掷后,每个数字被投中了多少次。
# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000 # 相对频率作为估计值
tensor([0.1650, 0.1650, 0.1720, 0.1750, 0.1610, 0.1620])
进行500组实验,每组抽取10个样本。
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();
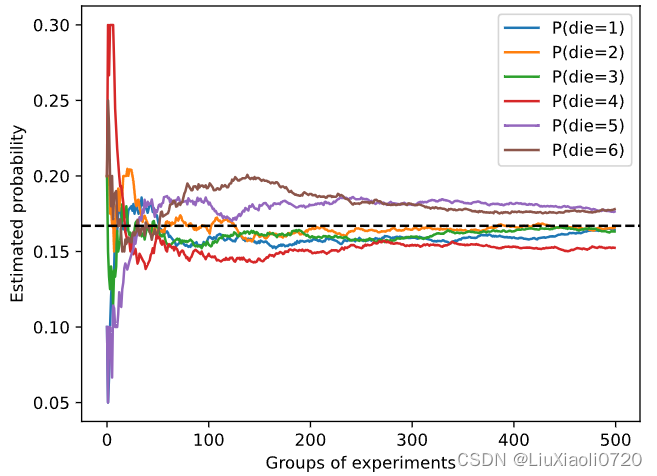
每条实线对应于骰子的6个值中的一个,并给出骰子在每组实验后出现值的估计概率。
当我们通过更多的实验获得更多的数据时,这
6
6
6条实体曲线向真实概率收敛。