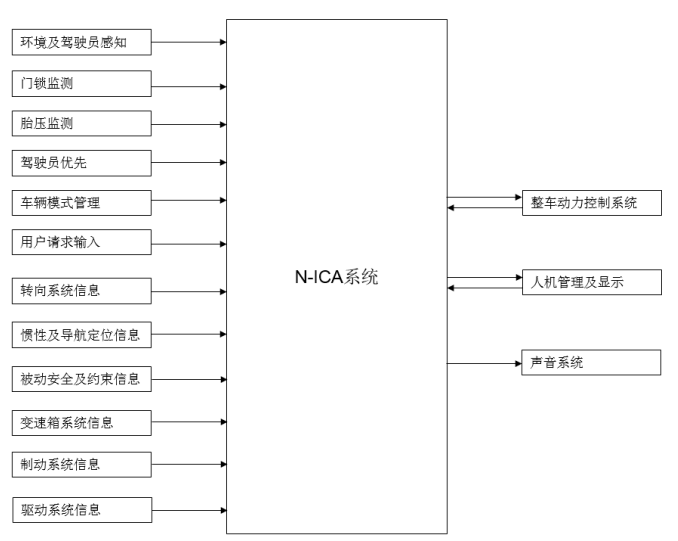
输入年月日,显示这一天是这一年的第几天,保证输入日期合法。
| 题干 | 输入年月日,显示这一天是这一年的第几天,保证输入日期合法。 | ||
| 输入样例 | 2022 1 1 2022 12 31 2024 12 31 2022 4 5 | ||
| 输出样例 | 2022-1 2022-365 2024-366 2022-95 | ||
#include<stdio.h>
int fun(int y, int m, int d) {
int a[12] = { 31,28,31,30,31,30,31,31,30,31,30,31 },i,s=0;
if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0)) {
a[1] += 1;
}
for (i = 0; i < m - 1; i++) {
s += a[i];
}
return s + d;
}
int main() {
int y, m, d,t;
while (~scanf("%d%*c%d%*c%d", &y, &m, &d)) {
t = fun(y, m, d);
printf("%d-%d\n", y,t );
}
return 0;
}求输入N段整数范围的素数之和。
| 题干 | 求输入N段整数范围的素数之和。 若输入: 3 11 18 5 10 3 7 则计算[11 18]之间的素数11,13,17,[5 10]之间的素数5,7,[3 7]之间的素数3,5,7,八个素数之和68。 | ||
| 输入样例 | 3 11 18 5 10 3 7 | ||
| 输出样例 | 68 | ||
#include<stdio.h>
#include<math.h>
int main() {
int i, n, l, r,s=0,j,k,a;
scanf("%d", &n);
for (i = 0; i < n; i++) {
scanf("%d%*c%d", &l, &r);
for (k = l; k <= r; k++) {
a = (int)sqrt(k);
for (j = 2; j <= a; j++) {
if (k % j == 0)
break;
}
if (j > a) {
s += k;
}
}
}
printf("%d", s);
return 0;
}求输入N段组合数之和。

#include<stdio.h>
int qjc(int n) {
if (n == 1)
return 1;
else
return qjc(n - 1) * n;
}
int qzh(int a, int b) {
return qjc(a) / (qjc(b) * qjc(a - b));
}
int main() {
int n, s = 0, a, b;
scanf("%d", &n);
while (n--) {
scanf("%d%*c%d", &a, &b);
s += qzh(a, b);
}
printf("%d\n", s);
return 0;
}输入n计算f(-n)+f(-(n-1))+...+f(-1)+f(0)+f(1)+...+f(n-1)+f(n)的和,f(x)计算公式如下,结果显示小数点后6位。

#include<stdio.h>
double f(int x) {
if (x == 0 || x == 2)
return 0;
else if (x > 0)
return (x + 1.0) / (x - 2);
else
return (x - 1.0) / (x * x);
}
double qh(int n) {
int i = -n;
double s = 0;
for (i = -n; i <= n; i++) {
s += f(i);
}
return s;
}
int main() {
int n,a, b;
scanf("%d", &n);
printf("%lf\n", qh(n));
return 0;
}输入整数n,使用梯形法求方程y=4-x*x与x轴构成图形的面积。n为梯形个数,n越大计算面积约精确。

#include<stdio.h>
double fun(double x) {
return 4 - x * x;
}
double qmj(double a, double b, int fs) {
double s = 0, dx = (b - a) / fs;
int i;
for (i = 0; i < fs; i++) {
s += (fun(a + i * dx) + fun(a + (i + 1) * dx)) * dx / 2;
}
return s;
}
int main() {
int n;
scanf("%d", &n);
printf("%lf\n", qmj(-2, 2, n));
return 0;
}