一、简介

1.1 定义

贪心算法（Greedy Algorithm），又名贪婪法，是寻找 最优解问题 的常用方法。

• 将求解过程 分成若干个步骤，每个步骤都应用贪心原则，选取当前状况下最好/最有的选择（局部最有利的选择），并以此希望最后堆叠出的结果也是最好/最优的解。

1.2 基本步骤

• 步骤1：从某个初始解出发；
• 步骤2：把求解的问题分成若干个子问题；
• 步骤3：对每一子问题求解，得到子问题的局部最优解；
• 步骤4：把子问题的局部最优解合成原来问题的一个解。

1.3 优缺点

优点：

• 简单、高效，省去为了寻找最优解可能需要穷举的操作，通常作为其他算法的辅助算法来使用；

缺点：

• 不从整体上考虑其它可能情况，每次选取局部最优解，不再进行回溯处理，所以 并非一定能得到整体最优解。

---

二、经典示例

2.1 选择排序

没错，我们常见的选择排序就是运用了贪心算法的思想。

题目：

• 实现数字数组递增排序。

解答：

从数组的零下标开始，依次从后面找到最小的元素下标与当前位置的元素互换，这个在后面寻找最小元素的过程就是贪心的思想。

贪心策略：寻找最小的元素，（贪心地）认定此元素就是当前位置的最小元素，然后遍历每一个位置。

public void choiceSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            minIndex = arr[j] < arr[minIndex] ? j : minIndex;
        }
        if (minIndex != i) {
            int tmp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = tmp;
        }
    }
}

2.2 背包问题

题目：

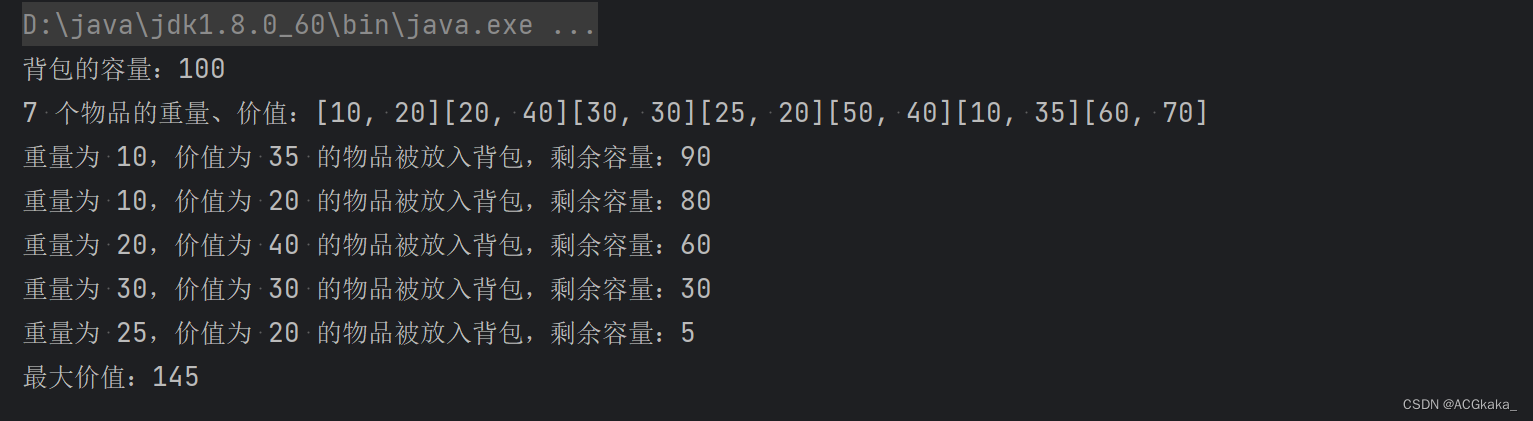
有一个背包，容量由你自己输入，有n个物品，每个物品都具有容量与价值，这些都是由你自己输入的，请问，要怎么放物品到背包里，才能使得总价值最大呢，放入背包的总容量要小于等于背包的总容量。（如果一个物品放不下，则可以拆分成多个小块）
背包：M：100
物品：N：7
重量 价值
10 20
20 40
30 30
25 20
50 40
10 35
60 70

解答：

每个物品都具有自己的重量与价格，不妨计算出每个物品的单位价值。

• 单位价值： 价值/重量，即每份重量的价值。

然后我们将这些物品 按照单位价值递减排序。这样一来就简单了，只需用贪心算法，依次把最大单位价值的物品价值和重量相加 就行了。

贪心策略：单位价值最大的物品，我们假设它就是最好的，直接把它放在背包里面。

public static void main(String[] args) {
    int[][] items = new int[7][2];
    items[0][0] = 10; items[0][1] = 20;
    items[1][0] = 20; items[1][1] = 40;
    items[2][0] = 30; items[2][1] = 30;
    items[3][0] = 25; items[3][1] = 20;
    items[4][0] = 50; items[4][1] = 40;
    items[5][0] = 10; items[5][1] = 35;
    items[6][0] = 60; items[6][1] = 70;
    int capacity = 100;
    System.out.println("背包的容量：" + capacity);
    StringBuilder builder = new StringBuilder();
    for (int[] item : items) {
        builder.append(Arrays.toString(item));
    }
    System.out.println(items.length + " 个物品的重量、价值：" + builder.toString());
    int maxValue = maxValue(items, capacity);
    System.out.println("最大价值：" + maxValue);
}

public static int maxValue(int[][] items, int capacity) {
    // 计算单位价值
    double[] prices = new double[items.length];
    Map<Double, List<Integer>> positionMap = new HashMap<>(items.length);
    for (int i = 0; i < items.length; i++) {
        prices[i] = 1.0 * items[i][1] / items[i][0];
        List<Integer> positions = positionMap.getOrDefault(prices[i], new ArrayList<>());
        positions.add(i);
        positionMap.put(prices[i], positions);
    }
    // 排序
    Arrays.sort(prices);
    int weight = 0;
    int maxValue = 0;
    for (int i = prices.length - 1; i >= 0; i--) {
        List<Integer> positions = positionMap.get(prices[i]);
        if (positions != null) {
            Integer position = positions.remove(0);
            if (positions.size() == 0) {
                positionMap.remove(prices[i]);
            }
            if (weight + items[position][1] < capacity) {
                weight += items[position][0];
                maxValue += items[position][1];
                System.out.println("重量为 " + items[position][0] + "，价值为 " + items[position][1] + " 的物品被放入背包，剩余容量：" + (capacity - weight));
            }
        }
    }
    return maxValue;
}

执行结果：

---

三、经典反例：找零钱

322. 零钱兑换

3.1 题目

假设你开了间小店，不能电子支付，钱柜里的货币只有 25 分、20分、10 分、5 分和 1 分 四种硬币，如果你是售货员且要找给客户 41 分钱的硬币，如何安排才能找给客人的钱既 正确 且硬币的个数又 最少？

3.2 解答

我们看到这种题目可能第一个想法就是用 贪心算法 进行解决，其实不然，由于贪心算法不能进行回溯处理，所以并不能取得最优解。

• 41 分钱按照贪心算法，先找 25分，剩余 16分，再找 10分、5分、1分，共需要 4 枚硬币。
• 实际情况下，我们只需要找两个 20分钱，再找一个 1分钱就够了，共需要 3 枚硬币。

那么不用贪心算法，应该用什么算法呢？其实有两种方法可以解决：

• 一是 贪心+回溯，即 记忆化搜索。
• 二是 动态规划。

3.3 记忆化搜索实现

• 记忆化搜索实现方式，就是自顶向下遍历，先查用完一枚硬币之后还剩多少钱，再根据剩余的钱进行迭代。

代码实现需要注意以下几点：

• int[] 类型数组初始化值为0；
• 针对需要记忆的组合，不光要记忆成功的情况，失败的情况也要记录。

class Solution {
	public static void main(String[] args) {
        int amount = 41;
        int[] arr1 = {1, 5, 10, 20, 25};
        System.out.println("零钱总数为：" + amount);
        System.out.println("硬币面值为：" + Arrays.toString(arr1));
        int result1 = coinChange(arr1, amount);
        System.out.println("最少使用硬币数：" + result1);
    }

    public static int coinChange(int[] coins, int amount) {
        if (amount == 0) {
            return 0;
        }
        return handleCoin(coins, new int[amount], amount);
    }

    private static int handleCoin(int[] coins, int[] his, int coinAmount) {
        if (coinAmount < 0) {
            return -1;
        }
        if (coinAmount == 0) {
            return 0;
        }
        if (his[coinAmount - 1] != 0) {
            return his[coinAmount - 1];
        }
        int minCount = Integer.MAX_VALUE;
        for (int coin : coins) {
            int tmpMinCount = handleCoin(coins, his, coinAmount - coin);
            if (tmpMinCount != -1 && tmpMinCount + 1 < minCount) {
                minCount = tmpMinCount + 1;
            }
        }
        his[coinAmount - 1] = minCount == Integer.MAX_VALUE ? -1 : minCount;
        return his[coinAmount - 1];
    }
}

执行结果：

3.4 动态规划实现

• 动态规划实现，则是自底向上，先计算从1开始每个金额所需的最小零钱数，直到找到需要的钱数，过程中对于剩余钱数所需要的最小零钱数可以直接使用前面计算好的数据。

代码实现需要注意以下几点：

• 对于数值类型的映射，不要用 Map 类型，用 int[] 类型效率更高；
• 在循环迭代的过程中，只需要加硬币数就可以了，不用再去迭代考虑其他的组合。

class Solution {
    public static void main(String[] args) {
        int amount = 41;
        int[] arr1 = {1, 5, 10, 20, 25};
        System.out.println("零钱总数为：" + amount);
        System.out.println("硬币面值为：" + Arrays.toString(arr1));
        int result1 = coinChange(arr1, amount);
        System.out.println("最少使用硬币数：" + result1);
    }

    public static int coinChange(int[] coins, int amount) {
        // k-零钱和，v-最小零钱量
        int[] his = new int[amount + 1];
        Arrays.fill(his, amount + 1);
        his[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (coin <= i) {
                    his[i] = Math.min(his[i], his[i - coin] + 1);
                }
            }
        }
        return his[amount] == amount + 1 ? -1 : his[amount];
    }
}

执行结果：

整理完毕，完结撒花~ 🌻

参考地址：

1.小白带你学—贪心算法（Greedy Algorithm)，https://zhuanlan.zhihu.com/p/53334049

2.贪心算法思想详解+示例代码，https://blog.csdn.net/jj6666djdbbd/article/details/126971331