可验证随机函数（VRF）

文章目录

- 一、背景以及场景
- - 共识发展
  - - 第一代 POW “以力取胜”
    - 第二代 POS/DPOS “民主投票”
    - 第三代 VRF “运气抽签”
- 二、可验证随机函数（VRF）快速开始
- - 1. VRF是什么?
  - 2. MD5 hash函数和VRF（Verifiable Random Function）区别
  - 3. VRF-可验证随机函数
- 参考

一、背景以及场景

在区块链场景中，有的框架会用算法随机产生出块节点与验证节点（如Algorand），甚至解决分叉。按传统的随机算法，按一定的哈希规则随机轮询，选出一个节点来记账/验证。如果这个随机轮询的规则是谁都可以复现的，那么可以推测出将来的某个记账/验证节点，集中攻击它。
为了解决这个问题，就引入了VRF，只有自己能够完成这个哈希过程，而别人只能在他声明之后验证这个过程，防止有人可以提前推测出将来的记账节点。

VRF的目的就是要生成随机值，且无法被预测，同时还要可验证，可重放。

共识发展

区块链新一代共识算法：VRF分布式可验证随机函数
参考URL: https://blog.csdn.net/wxid2798226/article/details/84316219

假设一个小岛，没有法币，由101个对等的没有隶属关系的记账人来记录小岛的经济活动（也就是所谓去中心化记账）。这样的设计，冗余性应该非常好，某个记账人出问题了不影响整个系统，最大的麻烦是这么多人同记一本账，而且没有中心化的统一指挥，会不会出现不同人记的不一致？以谁为准？那么不同人分布式各自记账的前提下，怎么用规则保证各自记的账相互核对是一致的？这个就是所谓共识问题

第一代 POW “以力取胜”

真实世界中，比特币和以太坊用的就是POW，以力量取胜（即芯片算力），目前已经发展了好几代专用芯片，消耗了巨额的设备购置资金，POW挖矿过程中也消耗了很多能源。另外，POW的性能也不好，比特币和以太坊的tps（每秒处理的事务）都不高。POW最大的优点是久经考验，比特币运行到现在十年了，POW算法证明是行之有效；以太坊POW运行到现在也好几年了，想换成其他算法一直没换成。可见POW现阶段是有其存在的道理的。

第二代 POS/DPOS “民主投票”

真实世界中，以太坊准备从POW换成POS，EOS的共识算法是DPOS（DPOS和POS的差别可以认为是间接民主和直接民主的区别，POS是一币一票直接投票；DPOS是一币一票先选举出人大代表，再由人大代表对具体议题投票）。实践中效果很一般：

POS虽然不浪费能源，但是别忘了人类社会永恒的不均衡性，很多时候，巨额财富只掌握在小部分人手里。以太坊大部分都只掌握在少数“巨鲸”手里，改成POS，小散没什么话语权，也不会取关心投票，建设生态，和去中心化的理念相违背
DPOS在EOS的实践也有待考验，目前看普通使用者也没有什么动力去投票，一是对被选举者不了解，二是投票也花费时间，更何况普通人的票也起不了太大作用，因为抵不上“巨鲸”手里一个零头。

第三代 VRF “运气抽签”

除了投票外，人类社会还有一个解决办法是抽签，不过不是排队轮流从一个筒子里面抽签（那样太中心化了，中心的那个抽签筒容易动手脚），而是每个人一个抽签桶，各自抽完了再亮相出来比大小，最小的为准；两人抽中同一个签，可以这两人再抽一轮。

那么怎么防止作弊呢？比如每个人都挑最小的签，然后宣称自己是抽中呢。这样的分布式抽签永远没有结果了。现实世界针对这样的问题，**采取一种叫做“零知识证明”的数学机制，没做实际抽签动作，是凑不出实际的结果的，也通不过大家的校验。**在区块链小岛上，你可以想象成，每个人边抽签边用手机录下抽签过程和轮次标志，如果大家有疑问可以回放录像。

总之，这个解决方案我感觉很接近于中本聪原来设想的那个区块链世界。不再有矿场和矿机浪费能源，损害去中心化；效率也很高；而且保证了尾部参与者也能有机会参与记账，有一定的公平性。下一代的共识算法已来。

POW靠蛮力取胜，中本聪设想的“一cpu一票”的乌托邦并没有到来，他忘记了人类社会的不均衡性，POW形成了一个个中心化的大矿场，利益的集中化导致普罗大众并不关心区块链；矿场主本身也是逐利而来，并不关心生态；资源和利益集中在少部分大矿场和大交易所手里，普罗大众只求炒币分一杯羹，结果被“割韭菜”。

DPOS也存在同样的问题，投票制度最早是希腊雅典在面对波斯人入侵时被发明出来决定是战是降的生死存亡问题（参见民主的起源）；DPOS现在投票率很低，票又集中在少数人手中，那些炒作eos的普通人有几个真正关心生态并花时间认真行使投票权？

**解决这个问题，需要长时间探索。也许抽签制的VRF是个解决方法。**至少这个制度下，尾部的参与者也是有可能获得利益的，利益分配没有像过去那么集中。

二、可验证随机函数（VRF）快速开始

1. VRF是什么?

VRF 这个概念最早由 Micali，Rabin 和 Vadhan 三个人所提出。
一句话描述：以sk和随机种子作为输入，输出伪随机数r和对应的证明proof
任何人可以通过sk对应的公钥vk加上证明proof来验证伪随机数r是否有sk持有者生成。

VRF是可验证随机函数(verifiable random function)，一方面具有伪随机性，另一方面它还具有可验证性(输出包括一个非交互零知识证明)

eg. 假设现在是round 10（第10 轮），节点们可能会轮流抽签，以节点自己的私钥+ 一个全网都知道的随机数（比如是这轮的轮次10）作为输入，生成了一个随机数（0-100）；设置一个条件：100 个节点轮流抽签，谁先抽出来的随机数大于10，就是这一轮的打包者。假设5 号节点抽到了11，可是只有5 号知道其他人不知道，因此他在广播这个随机的同时还需要广播一个零知识证明。通过零知识证明，全网只需要通过5 号的公钥就可以验证，接受5 号为这轮打包者。

在这里插入图片描述

在这里插入图片描述

关于第三步：验证
验证函数 Verify 输入验证密钥 vk、消息 x 以及伪随机y和证明π \piπ。输出结果0/1：只有该函数验证了证明 π \piπ 是根据 x 生成的，且根据证明π \piπ可以推导出 Y，才会输出 1，也就是说该函数验证 X 与 Y 是否存在唯一的对应关系。

所谓VRF就是指给定一个消息和一个私钥，可以计算出一个唯一确定的值，这个值唯一确定且不可预测，且可以验证。
传统的签名算法不具有唯一确定的特性，私钥持有者可以计算出多个合法解。

VRF 和伪随机函数功能类似,通过任意一个输入,可以获得一个随机数输出:

对于不同的输入,输出是随机的,并且均匀分布在值域范围内.
对于相同的输入,得到的输出是相同的
但相比于伪随机函数,VRF 多了一个非交互的零知识证明,使用私钥和输入生成proof,其他人可以使用公钥和输入来验证随机数输出的正确性.

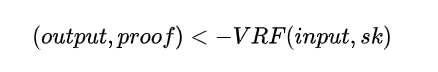
在这里插入图片描述
input 为合法输入,sk 是用户的私钥,output 是输出的随机数,proof 可以证明输出的数据合法.

在这里插入图片描述

2. MD5 hash函数和VRF（Verifiable Random Function）区别

MD5 hash函数和VRF（Verifiable Random Function）确实有相似之处，他们都会对相同的输入产生相同的输出。但是，他们之间的主要区别在于VRF具有可验证性。

具体来说，VRF生成的输出不仅与输入有关，还与特定的私钥有关。并且，VRF在生成输出的同时，还会生成一个证明。这个证明可以被任何人使用对应的公钥来验证，以确保输出是由特定的私钥和输入生成的。这就是所谓的"可验证性"，它是MD5等普通hash函数不具备的。

另外，VRF的输出具有随机性，即它的输出在所有可能的输出空间中是均匀分布的。这使得VRF的输出可以被用作随机数。而MD5等普通hash函数虽然能够生成固定长度的输出，但是这些输出并不一定具有良好的随机性。

因此，尽管MD5 hash函数和VRF在某些方面有相似之处，但是VRF由于具有可验证性和输出的随机性，使其在很多应用中更具优势。

3. VRF-可验证随机函数

VRF-可验证随机函数
参考URL: https://blog.csdn.net/yhc166188/article/details/100188559
可验证随机函数VRF
参考URL: https://blog.csdn.net/shangsongwww/article/details/88813116

VRF(Verifiable Random Function)：可验证随机函数用于区块链中的意义很好理解——用以完成出块节点的随机选择。

VRF算法作为一种基于密码学的新型共识模型，最大的优势是快速共识、抗攻击能力、极低算力需求，已有的解决方案有Algorand算法和Dfinity中基于BLS的算法等。

result = SHA256(secret,info)

上面的函数，要想得到结果result，需要secret和info，要验证result，也需要secret和info，也就是说需要知道secret才能验证info和result是否对应匹配。

有没有可能在不出示secret的情况下，验证result和info是否对应匹配。这就是可验证随机函数VRF可以做到的。

result = VRF_HASH(SK,info)

其中SK表示secret key，是私钥，不对外公开的，自己秘密保存即可。与SK配对的PK表示public key，是公钥，需要公开给验证着的。有了上面这些基本的元素，具体的VRF操作流程就非常简单清晰了：

1.证明者生成一对秘钥，PK和SK；
2.证明者计算result = VRF_HASH(SK,info)；
3.证明者计算proof = VRF_Proof(SK,info);
4.证明者把result和proof递交给验证者;
5.验证者计算result = VRF_P2H(proof)是否成立，若成立，继续，否则中止；
6.证明者把PK，info递交给验证者；
7.验证者计算True/False = VRF_Verify(PK,info,proof),True表示验证通过，False表示验证未通过。

验证通过，指proof是否是通过info生成的，通过proof是否可以计算出result，从而推导出info和result是对应匹配的。从上面可以看出，验证者并没有获得证明者的私钥SK，验证者同样可以推导出info和result是否对应匹配，这就是VRF的妙用。

对哈希函数的不断演化，可以简单用如下的路径来表示：

原始的哈希函数: info -> result 

带秘钥的哈希函数： info,secret -> result

公钥版本的VRF： info,SK -> proof,PK -> result

参考

VRF介绍
参考URL: https://blog.csdn.net/shangsongwww/article/details/88797403
Chainlink 预言机教程（原理讲解 & 代码演示）
参考URL: https://www.bilibili.com/video/BV1ed4y1N7Uv/
Chainlink 预言机的原理解析
参考URL: https://learnblockchain.cn/article/4766