在线平台GAMES链接

Lecture1 Overview of CG 计算机图形学概述

计算机图形学主题: 学习图形学，而不是图形学API(如OPENGL)

• Rasterization(光栅化)
• Curves and Meshes(曲线和曲面)
• Ray Tracing(光线追踪)
• Animation/Simulation(动画和仿真)

Lecture2 Review of Linear Algebra 向量与线性代数

（高中数学足矣，重要的是这些公式在图形学中的应用）
（列）向量 AB=B-A
向量标准化: 单位向量= a / ||a||
向量加法
向量点乘 ：ab=||a||||b||cosγ，用于提供两个向量是否接近
向量叉乘 ：axb=||a||||b||sinγ (方向右手定则)，用于判断左右(两个向量的左右)/内外(三角形内外)
直角坐标系
矩阵运算

Lecture3 2D Transformation 基础变换（二维）

3.1 线性变换 (寻找变换前后直角坐标坐标关系)

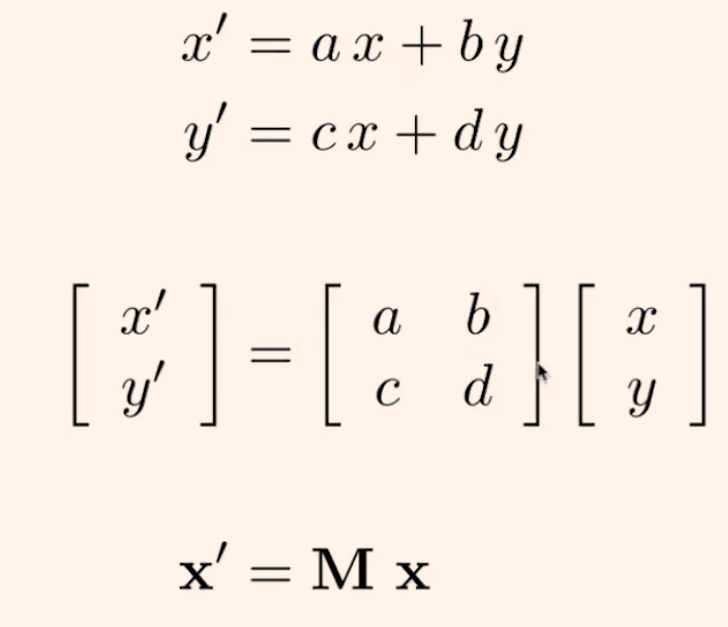
非均匀缩放

反射

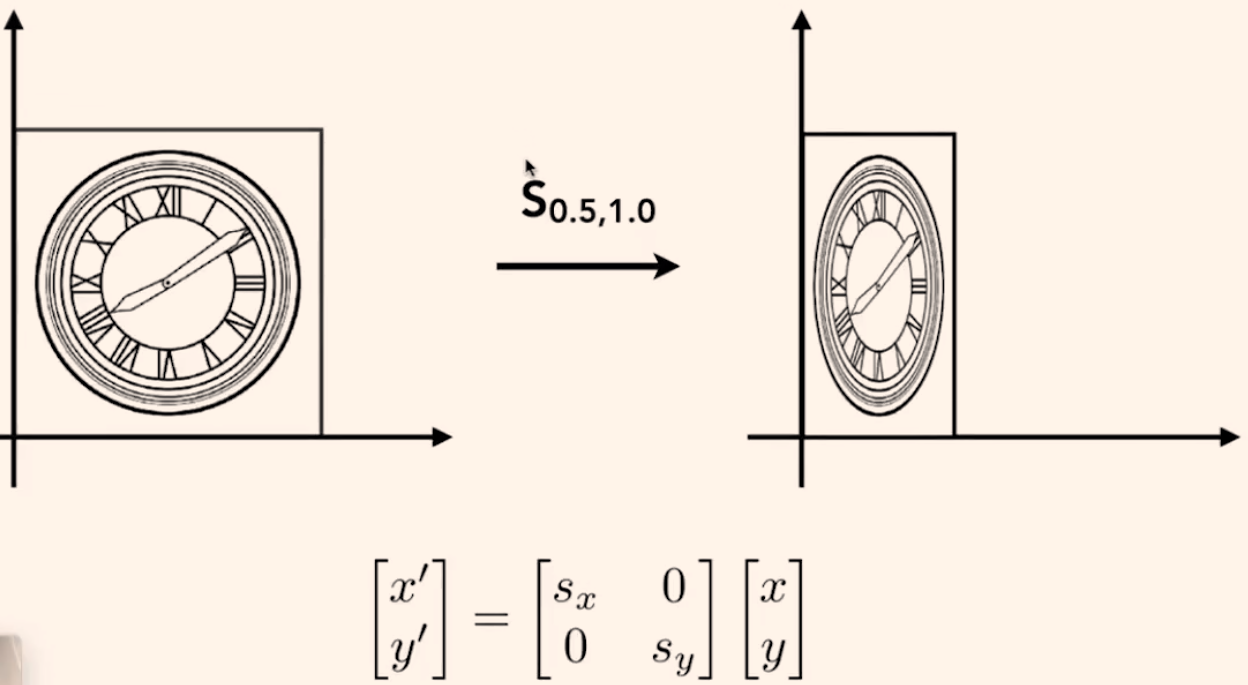
切变

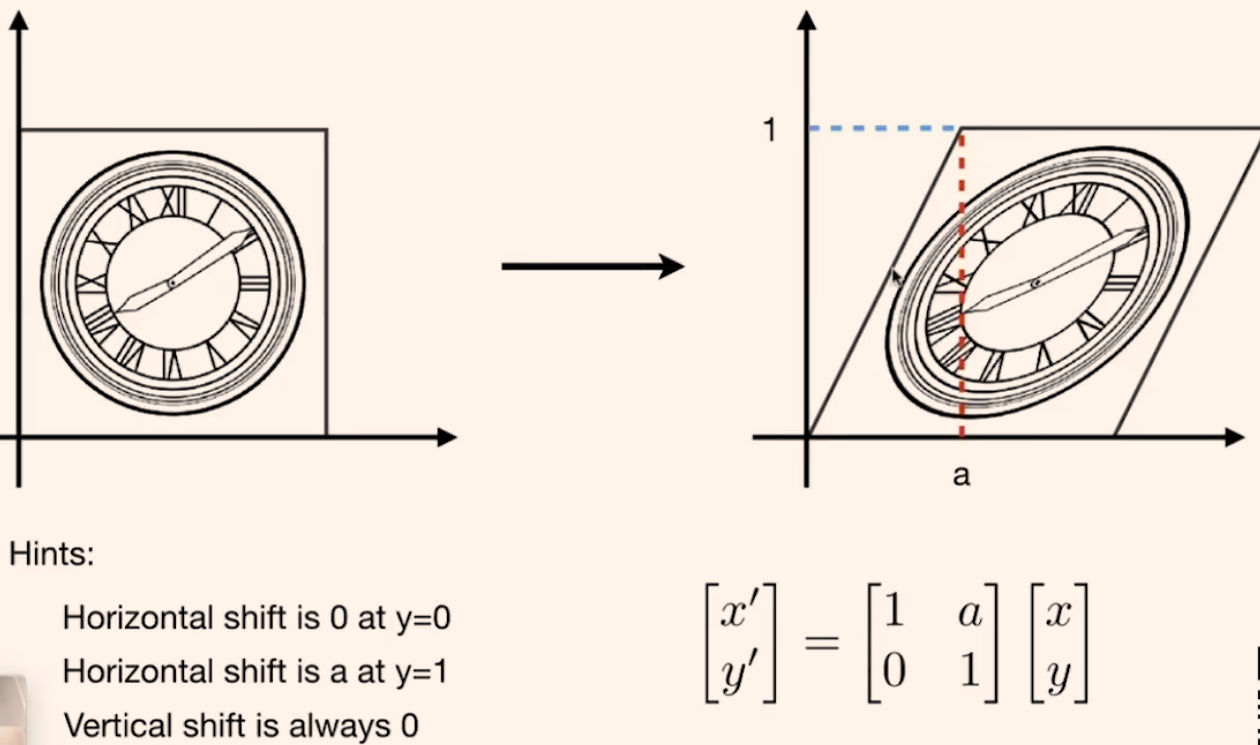
旋转(绕原点，逆时针) 旋转矩阵记忆法：行列式=1

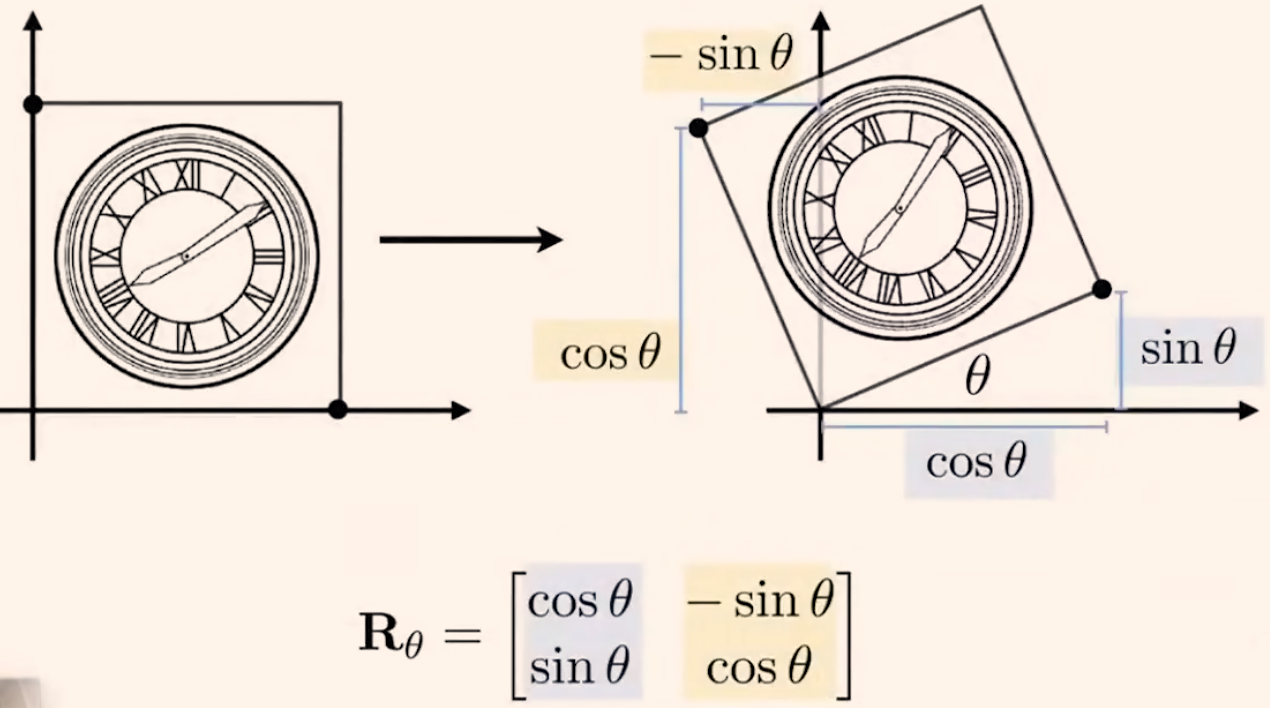
3.2齐次坐标 Homogeneous Coordinate

引入原因：普通直角坐标系中，平移不能写成矩阵乘法，不属于线性变换。引入齐次坐标：就可以将 线性变换 和 平移变换，即所有变换，统一用矩阵乘法表示。

齐次坐标：相比于普通直角坐标，点和向量都增加一个维度，点的第三维=1，向量的第三维=0.

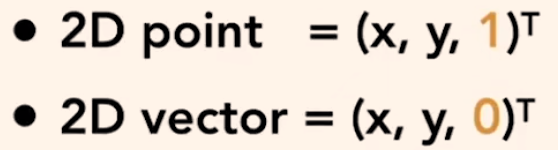
V+V=V，P-P=V，P+V=P，P+P=中点

结论：(x, y, w) = (x/w, y/w, 1)

平移变换(齐次坐标表示)： 妙

3.3 仿射变换Affine Transformations

2D仿射变换：所有线性变换+平移变换的综合体，用齐次坐标的矩阵乘法即可统一，最后一行永远是(0,0,1)。

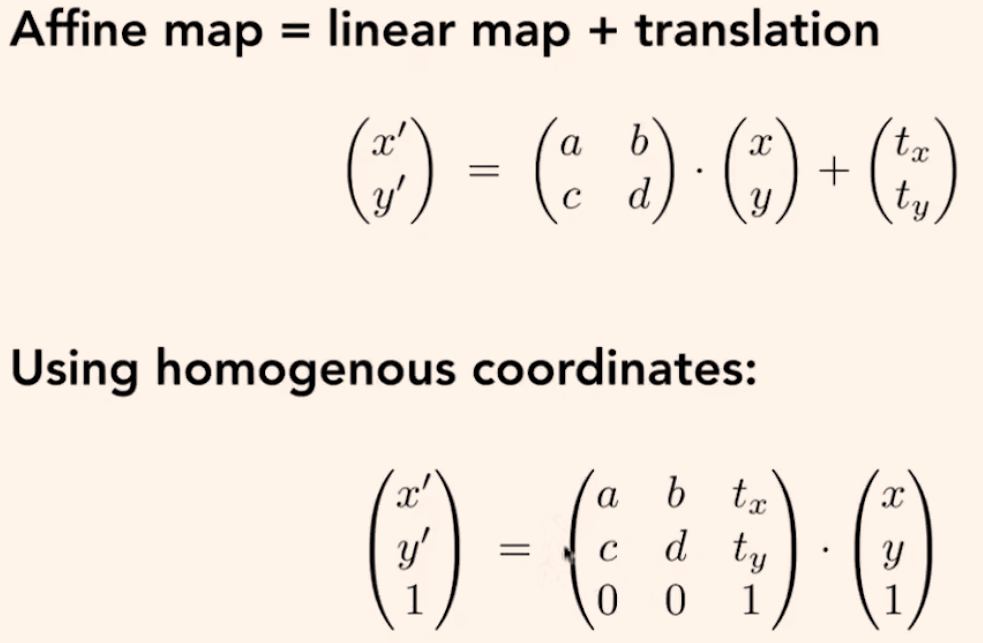
2D缩放/旋转/平移的仿射变换矩阵

3.4 逆变换

用仿射变换矩阵乘法表示，相当于乘变换矩阵M的逆矩阵。

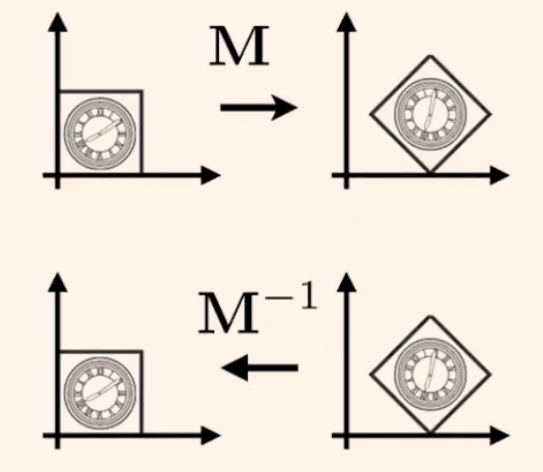
3.5 复合变换

复杂的变换可以通过简单的变换组合而成（通过矩阵的多次乘法实现），但变换的顺序很重要（即矩阵乘法顺序很重要，矩阵乘法没有交换律），向量是列向量，矩阵放左边，多个矩阵从右到左应用到向量上。
多个变换矩阵Ai一个一个应用(变换的分解) 等价于 一个复合变换矩阵An…A1一次性应用(变换的复合)

Lecture4 3D Transformation 基础变换（三维）

4.1 3D齐次坐标

同样引入齐次坐标：相比于普通直角坐标，点和向量都增加一个维度，点的第三维=1，向量的第三维=0.

结论：(x, y, z, w) = (x/w, y/w, z/w, 1)

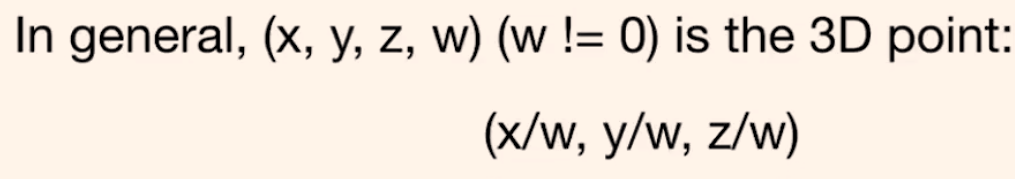
4.2 3D仿射变换

三维到二维变换（模型、视图、投影）
光栅化（离散化三角形）
光栅化（深度测试与抗锯齿）
着色（光照与基本着色模型）
着色（着色频率、图形管线、纹理映射）
几何（基本表示方法）
几何（曲线与曲面）
几何（前沿动态）
光线追踪（基本原理）
光线追踪（加速结构）
路径追踪与光的传播理论
复杂外观建模与光的传播、实时光线追踪（前沿动态）
相机、透镜与光场
颜色与感知
动画与模拟（基本概念、逆运动学、质点弹簧系统）
物质点法（前沿动态）