每日一题系列(day 04)
前言:
🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈
🔎🔎如果说代码有灵魂,那么它的灵魂一定是👉👉算法👈👈,因此,想要写出💚优美的程序💚,核心算法是必不可少的,少年,你渴望力量吗😆😆,想掌握程序的灵魂吗❓❗️那么就必须踏上这样一条漫长的道路🏇🏇,我们要做的,就是斩妖除魔💥💥,打怪升级!💪💪当然切记不可😈走火入魔😈,每日打怪,日日累积,终能成圣🙏🙏!开启我们今天的斩妖之旅吧!✈️✈️
因为这两题具有很强的相似性,所以将两题放在一起。
一、LeetCode-107.二叉树的层序遍历 II
题目:
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例1:
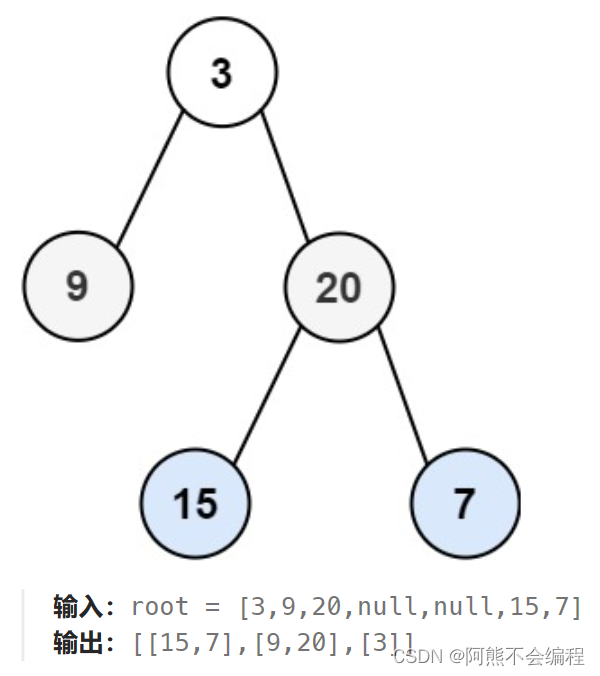
示例2:

注意事项:
- 树中节点数目在范围 [0, 2000] 内
- -1000 <= Node.val <= 1000
思路:
本题和昨天写的题很像,只不过这次的层序遍历是要从叶子结点所在层向上进行层序遍历,既然我们使用二维数组来进行层序遍历,我们不妨先将正常的层序遍历保存到二维数组中,在正常的层序遍历完成之后,将二维数组的元素(一维数组,存的是每一层节点的值)首尾交换。
我们再来回顾一下昨天说的二叉树层序遍历深搜的过程。
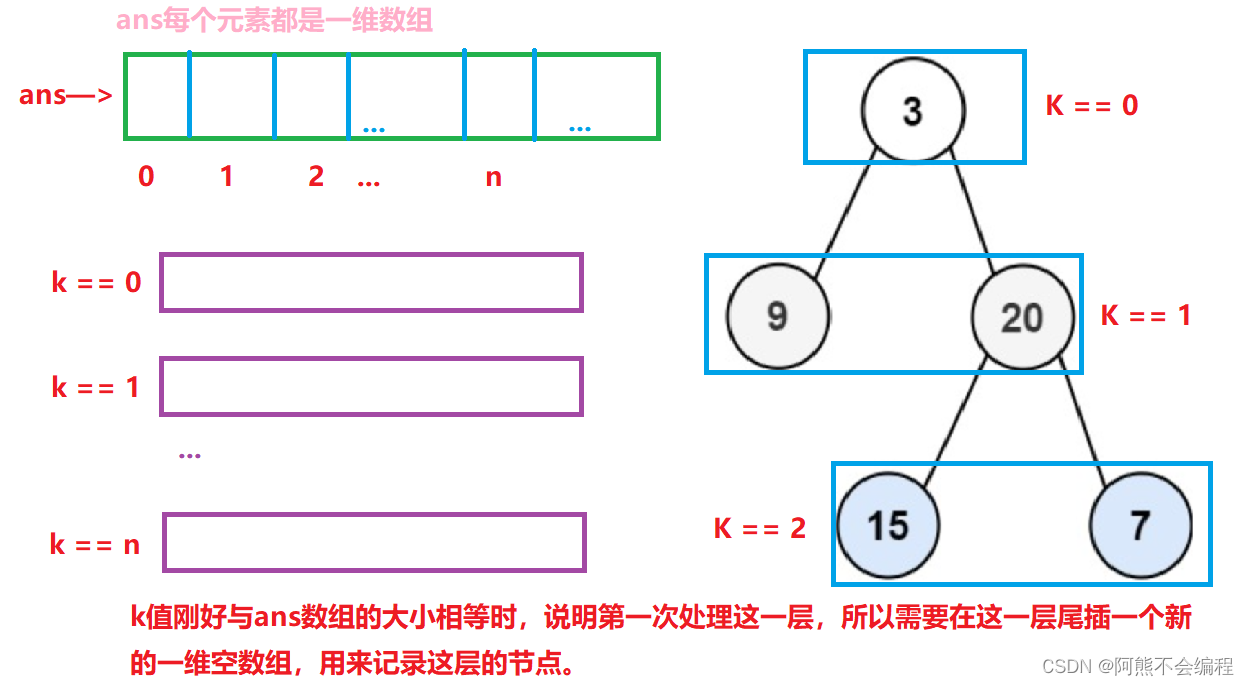
1、深搜需要传入参数root, 从哪层开始处理的层数,二维数组ans,在dfs中,首先判断当前节点是否为空,如果为空就return;
2、不过当前节点不为空,接下来就判断当前层数是否是最新遍历到的层数,如果是,在本层数组里压入元素之前需要创建一个空一维数组尾插到二维数组ans中。
3、接下来就是将当前处理节点压入到对应层数的一维数组中,这个节点处理完毕,深搜就要开始递归处理,先向左子孩子处理,下一层为本层节点+1,所以传参层数为k + 1,同理右子树也是如此,最后返回即可。
&emsp:4、深搜完成之后,我们就得到了一个自顶向下的层序遍历结果,我们想让结果自底向上遍历,只需ans的一维数组进行首尾交换,最后返回即可。
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void dfs(TreeNode *root, int k, vector<vector<int>> &ans)//深搜方式进行层序遍历
{
if(root == NULL) return;
if(k == ans.size()) ans.push_back(vector<int>());
ans[k].push_back(root -> val);
dfs(root -> left, k + 1, ans);
dfs(root -> right, k + 1, ans);
return;
}
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ans;
dfs(root, 0, ans);//先将正常的层序遍历拿到
for(int i = 0, j = ans.size() - 1; i < j ; i++, j--)//翻转正常的层序遍历,达到想要的效果
{
swap(ans[i], ans[j]);
}
return ans;//最后返回数组即可
}
};
一、LeetCode-103.二叉树的锯齿形层序遍历
题目:
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例1:
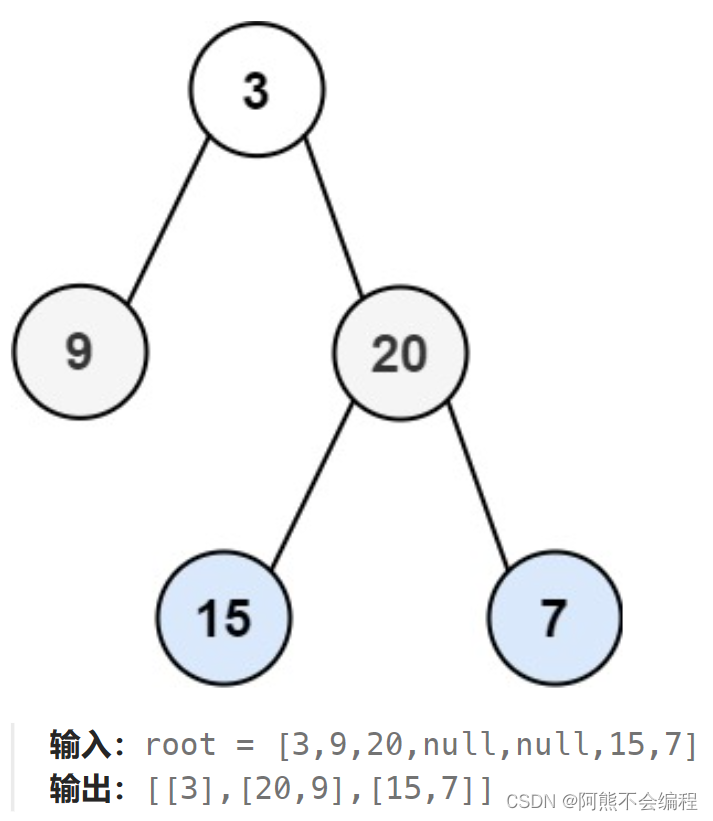
示例2:

思路:
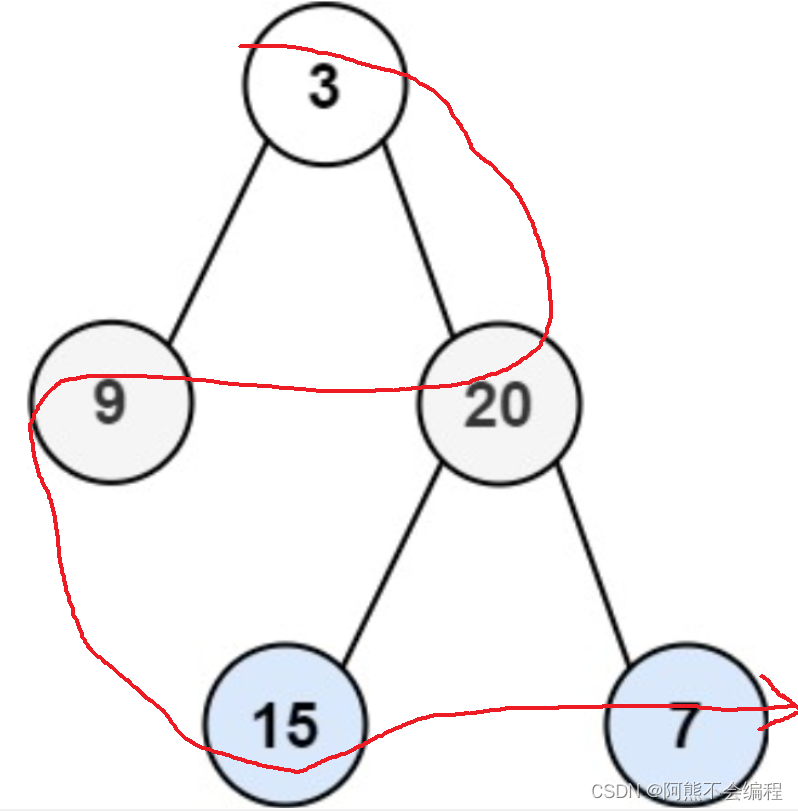
这题要求我们层序遍历要螺旋遍历,第一层从左到右遍历这一层节点,第二层从右到左遍历这层节点,第三层还是从左到右…遍历呈现出一种螺旋型遍历。
其实我们和上面107题一样,只需要先用深搜将正常的层序遍历结果拿到,在处理这个层序遍历的结果,拿到了正常层序遍历结果,我们来观察:
我们可以发现,我们遍历时需要翻转的总是偶数层,所以我们翻转的时候只需要处理偶数层的一维数组就可以了。
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void dfs(TreeNode *root, int k, vector<vector<int>> &ans)
{
if(root == NULL) return;
if(k == ans.size()) ans.push_back(vector<int>());
ans[k].push_back(root -> val);
dfs(root -> left, k + 1, ans);
dfs(root -> right, k + 1, ans);
return;
}
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ans;
dfs(root, 0, ans);//深搜
for(int k = 1 ; k < ans.size() ; k += 2)//偶数层才翻转
{
for(int i = 0, j = ans[k].size() - 1 ; i < j ; i++, j--)//将需要翻转的层进行翻转
{
swap(ans[k][i], ans[k][j]);
}
}
return ans;//返回翻转后的数组即可
}
};
这两题的相似度很高,我这里都是使用深搜的方式得到正常层序遍历的结果,当然你可以使用队列的形式得到层序遍历结果,这里就不展示了,这两题的不用是对层序遍历的结果的处理,转换成另外的形式。