基于斑马算法优化概率神经网络PNN的分类预测 - 附代码

摘要：针对PNN神经网络的光滑因子选择问题，利用斑马算法优化PNN神经网络的光滑因子的选择，并应用于变压器故障诊断。

1.PNN网络概述

概率神经网络（ probabilistic neural networks , PNN ）是 D. F. Specht 博士在 1 989 年首先提出的，是一种基于 Bayes 分类规则与 Parzen窗的概率密度面数估计方法发展而来的并行算 法。它是一类结胸简单、训练简洁、应用广泛的人工神经网络 。在实际应用中，尤其是在解决分类问题的应用中， PNN 的优势在于用线性学习算法来完成非线性学 习算法所傲的工作，同 时保持非线性算法的高精度等特性；这种网络对应的权值就是模式样本的分布，网络不需要训练，因而能够满足训练上实时处理的要求。

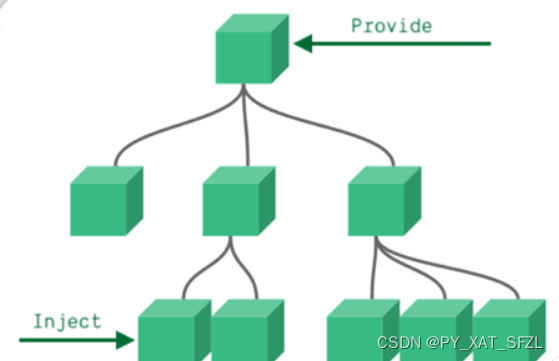
PNN 网络是由径向基函数网络发展而来的一种前馈型神经网络，其理论依据是贝叶斯最小风险准则（即贝叶斯决策理论）， PNN作为径向基网络的一种，适合于模式分类。当分布密度 SPREAD 的值接近于 0 时，它构成最邻分类器； 当 SPREAD 的值较大时，它构成对几个训练样本的临近分类器 。 PNN 的层次模型，由输入层、模式层、求和层、输出层共 4 层组成 ， 其基本结构如图 1 所示。
$$f(X,w_i)=exp[-(X-w_i{)}^T(X-W_i)/2\delta ]\text{\hspace{1em}(1)}$$
式中，$w_i$为输入层到模式层连接的权值 ；$\delta$为平滑因子，它对分类起着至关重要的作用。第 3 层是求和层，是将属于某类的概率累计 ，按式（1）计算 ，从而得到故障模式的估计概率密度函数。每一类只有一个求和层单元，求和层单元与只属于自己类的模式层单元相连接，而与模式层中的其他单元没有连接。因此求和层单元简单地将属于自己类的模式层单元 的输出相加，而与属于其他类别的模式层单元的输出无关。求和层单元的输出与各类基于内 核的概率密度的估计成比例，通过输出层的归一化处理 ， 就能得到各类的概率估计。网络的输 出决策层由简单的阔值辨别器组成，其作用是在各个故障模式的估计概率密度中选择一个具 有最大后验概率密度的神经元作为整个系统的输出。输出层神经元是一种竞争神经元，每个神经元分别对应于一个数据类型即故障模式，输出层神经元个数等于训练样本数据的种类个 数，它接收从求和层输出的各类概率密度函数，概率密度函数最大的那个神经元输出为 1 ，即 所对应的那一类为待识别的样本模式类别，其他神经元的输出全为 0 。

图1.PNN网络结构

2.变压器故障诊街系统相关背景

运行中的变压器发生不同程度的故障时，会产生异常现象或信息。故障分析就是搜集变压器的异常现象或信息，根据这些现象或信息进行分析 ，从而判断故障的类型 、严重程度和故障部位 。 因此 ， 变压器故障诊断的目的首先是准确判断运行设备当前处于正常状态还是异常状态。若变压器处于异常状态有故障，则判断故障的性质、类型和原因 。 如是绝缘故障、过热故障还是机械故障。若是绝缘故障，则是绝缘老化 、 受潮，还是放电性故障 ；若是放电性故障又 是哪种类型的放电等。变压器故障诊断还要根据故障信息或根据信息处理结果，预测故障的可能发展即对故障的严重程度、发展趋势做出诊断；提出控制故障的措施，防止和消除故障；提出设备维修的合理方法和相应的反事故措施；对设备的设计、制造、装配等提出改进意见，为设备现代化管理提供科学依据和建议。

2.1 模型建立

本案例在对油中溶解气体分 析法进行深入分析后，以改良三比值法为基础，建立基于概率神经网络的故障诊断模型。案例数据中的 data. mat 是 33 × 4 维的矩阵，前3列为改良三比值法数值，第 4 列为分类的输出，也就是故障的类别 。 使用前 23 个样本作为 PNN 训练样本，后10个样本作为验证样本 。

3.基于斑马优化的PNN网络

斑马算法原理请参考：https://blog.csdn.net/u011835903/article/details/130565746

利用斑马算法对PNN网络的光滑因子进行优化。适应度函数设计为训练集与测试集的分类错误率：
f i t n e s s = a r g m i n { T r a i n E r r o r R a t e + P r e d i c t E r r o r R a t e } (2) fitness = argmin\{TrainErrorRate + PredictErrorRate\}\tag{2} fitness=argmin{TrainErrorRate+PredictErrorRate}(2)

适应度函数表明，如果网络的分类错误率越低越好。

5.测试结果

斑马参数设置如下：

%% 斑马参数
pop=20; %种群数量
Max_iteration=20; %  设定最大迭代次数
dim = 1;%维度，即权值与阈值的个数
lb = 0.01;%下边界
ub = 5;%上边界

从结果来看，斑马-pnn能够获得好的分类结果。

6.参考文献

书籍《MATLAB神经网络43个案例分析》，PNN原理部分均来自该书籍

7.Matlab代码