力扣日记:【二叉树篇】对称二叉树
日期:2023.11.25
参考:代码随想录、力扣
101. 对称二叉树
题目描述
难度:简单
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
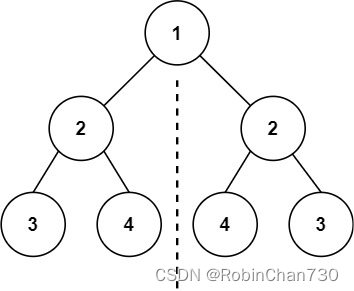
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
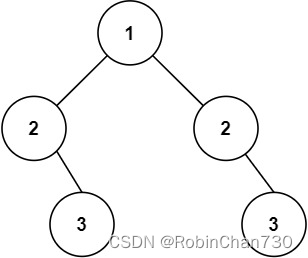
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围 [1, 1000] 内
- -100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
#define SOLUTION 1
public:
#if SOLUTION == 0
bool isSymmetric(TreeNode* root) {
/* // 错误的做法
// 示例1:前:1234243, 中:3241423, 后:3424321,层:1223443
// 示例2:中:12323,层:12233
// 层序遍历不行,只能中序遍历
// 使用栈,元素先进栈,遇到相同的则弹出
// 还是不能用值来判断是否对称....如果树上节点的值都是相等的,那就无法判断了...
stack<int> st_check; // 用来判断
// 中序遍历:左中右
// 对于中序遍历,访问和处理并不是同步进行的。而是先访问到最底层的左节点,再开始处理(入栈判断)
// 使用 cur 指针 先进行访问(遍历)
// if (root == NULL) return true;
stack<TreeNode*> st; // 用来遍历
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) { // 指针访问节点,先遍历到最底层
st.push(cur); // 将cur入栈
cur = cur->left; // 左
} else { // 处理
cur = st.top(); // 中 (处理:放入result数组)
st.pop();
if (cur != root) { // 根节点不入栈判断
if (st_check.empty() || st_check.top() != cur->val) st_check.push(cur->val); // 空或不相等则入栈
else st_check.pop(); // 相同则弹出
}
cur = cur->right; // 右 (如果右节点不为空,则在下次循环把右节点入栈;否则从栈中弹出顶部节点)
}
}
return st_check.empty();
*/
}
#elif SOLUTION == 1 // 递归遍历
/*
思路:判断二叉树是否对称 -> 通过判断二叉树能否左右翻转
分别比较外侧与内侧是否相等,即左节点的外侧(左孩子)需与对应右节点的外侧(右孩子)相等,内测同理
采用的遍历方式为后序遍历 -> 后序:左右中 -> 在左右子树都判断好是否能左右翻转后,再将信息传递到父节点(中),中节点作为左孩子或右孩子又继续向上传递
*/
bool compare(TreeNode* left, TreeNode* right) {
// 递归三要素1:参数与返回值:参数为当前层的左节点和对应右节点,返回值为两者的子树能否相互翻转(注意是子树,不包括自身,尽管只有当左和对应右节点相等才有继续比较的必要)
// 递归三要素2:终止条件:
// 1) 左右都为空:返回true
if (left == NULL && right == NULL) return true;
// 2) 左为空右不为空 或 左不为空右为空:返回false
else if ((left != NULL && right == NULL) || (left == NULL && right != NULL)) return false;
// 3) 左右不为空且左右值不相等
else if (left->val != right->val) return false;
// 递归三要素3:处理逻辑:如果左右值相等,则递归向下判断
else { // 由此可见:左右子树均为后序遍历
// 外侧:
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
// 内侧:
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
// 将外侧内侧的比较结果向上传递(给中节点)
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame; // 当外侧和内侧的子节点都分别相等,则当前left和right的子树是可以翻转的
}
}
bool isSymmetric(TreeNode* root) {
return compare(root->left, root->right);
}
#elif SOLUTION == 2 // 迭代法(队列)
bool isSymmetric(TreeNode* root) {
// 思路:
// 遍历:将左侧节点和对应右侧节点成对放入队列;
// 处理:再在弹出时成对弹出比较是否相等,相等则继续遍历子节点,否则终止
queue<TreeNode*> q;
if (root != nullptr) { // 先把根节点的左右节点放入队列
q.push(root->left);
q.push(root->right);
}
while (!q.empty()) {
// 成对弹出
TreeNode* leftSide = q.front(); q.pop();
TreeNode* rightSide = q.front(); q.pop();
// 比较
if (!leftSide && !rightSide) continue; // 左右都为空(没有子节点,则继续弹出)
// 左右有一个为空 或 左右都不为空但不相等,则肯定不对称,返回false
else if (!leftSide || !rightSide || (leftSide->val != rightSide->val)) return false;
// 如果相等,则继续遍历,将子节点入队列
q.push(leftSide->left);
q.push(rightSide->right); // 注意要成对:左的左 与 右的右
q.push(leftSide->right);
q.push(rightSide->left); // 左的右 与 右的左
}
return true;
}
#elif SOLUTION == 3 // 迭代法(栈)
bool isSymmetric(TreeNode* root) {
// 思路与队列类似,也是成对入栈、成对弹出、成对比较(队列更好理解……)
stack<TreeNode*> st;
if (root != nullptr) { // 先把根节点的左右节点放入队列
st.push(root->left);
st.push(root->right);
}
while (!st.empty()) {
// 成对弹出
TreeNode* rightSide = st.top(); st.pop();
TreeNode* leftSide = st.top(); st.pop();
// 比较
if (!leftSide && !rightSide) continue; // 左右都为空(没有子节点,则继续弹出)
// 左右有一个为空 或 左右都不为空但不相等,则肯定不对称,返回false
else if (!leftSide || !rightSide || (leftSide->val != rightSide->val)) return false;
// 如果相等,则继续遍历,将子节点入队列
st.push(leftSide->left);
st.push(rightSide->right); // 注意要成对:左的左 与 右的右
st.push(leftSide->right);
st.push(rightSide->left); // 左的右 与 右的左
}
return true;
}
#endif
};
复杂度
时间复杂度:
空间复杂度: