Leetcode 剑指 Offer II 054. 把二叉搜索树转换为累加树

news2024/11/18 7:45:52

题目难度: 中等

原题链接

今天继续更新 Leetcode 的剑指 Offer（专项突击版）系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~

题目描述

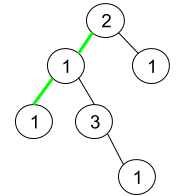
给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

输入：root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 10^4 之间。
每个节点的值介于 -10^4 和 10^4 之间。
树中的所有值互不相同。
给定的树为二叉搜索树。

题目思考

如何利用二叉搜索树的性质?

解决方案

思路

根据题目描述, 要将树的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和, 我们需要知道有哪些节点大于等于该节点
结合二叉搜索树的性质, 其中序遍历的节点是从小到大有序的, 自然其逆向中序遍历的节点就是从大到小有序的
我们可以利用这一点, 对树进行逆向中序遍历, 也就是先遍历右子树, 然后是当前节点, 最后是左子树
同时维护一个后缀和, 遍历到某个节点时, 就将它的值累加到该后缀和里, 那么该后缀和就是树中大于或者等于当前节点值的所有节点值之和, 将当前节点的值更新为该后缀和即可
最终遍历结束时, 树中所有节点的值就都更新好了, 直接返回根节点即可
下面代码中有详细的注释, 方便大家理解

复杂度

时间复杂度 O(N): 只需要遍历每个节点一次
空间复杂度 O(H): 递归调用最多使用 O(H) 栈空间, H 是树的高度

代码

class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        # 逆向中序遍历+后缀和
        # sm是当前遍历过的所有节点的后缀和
        sm = 0

        def revInorder(root):
            nonlocal sm
            if not root:
                return
            # 逆向中序遍历, 先遍历右子节点
            revInorder(root.right)
            # 后缀和加上当前节点值, 因为题目要求的是大于等于
            sm += root.val
            # 将当前节点值更新为后缀和
            root.val = sm
            revInorder(root.left)

        revInorder(root)
        return root