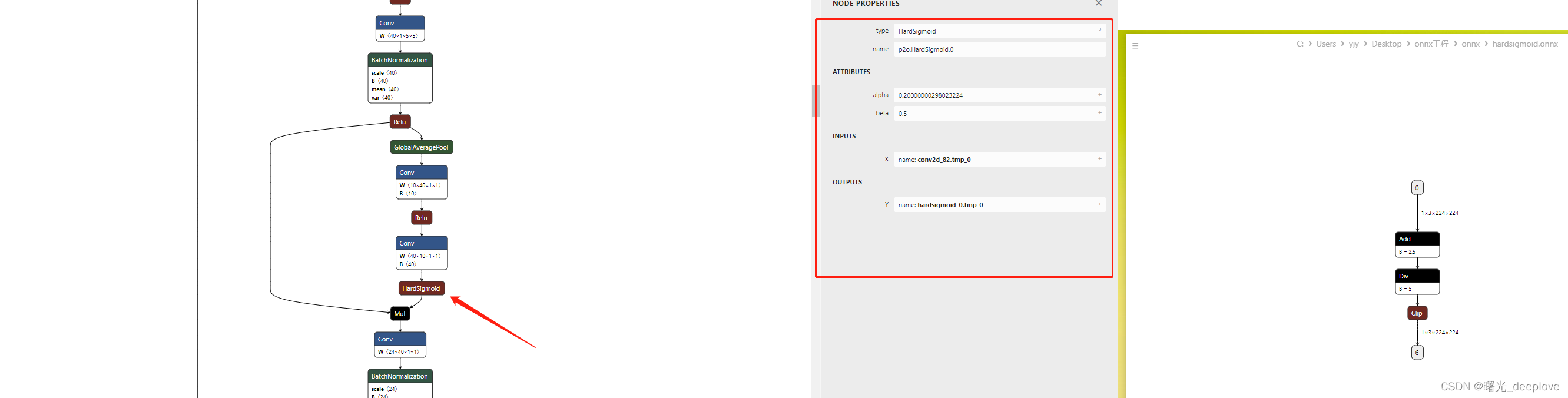
ruoyi-vue-plus5.x 后端
ruoyi-vue-plus5.x 前端
前端本地启动命令
# 克隆项目
git clone https://gitee.com/JavaLionLi/plus-ui.git
# 安装依赖
npm install --registry=https://registry.npmmirror.com
# 启动服务
npm run dev
# 构建生产环境 yarn build:prod
# 前端访问地址 http://localhost:80
docker部署
- idea环境配置
- 应用部署
遇到的问题
idea连接eidocker 运行 提示错误
重连docker

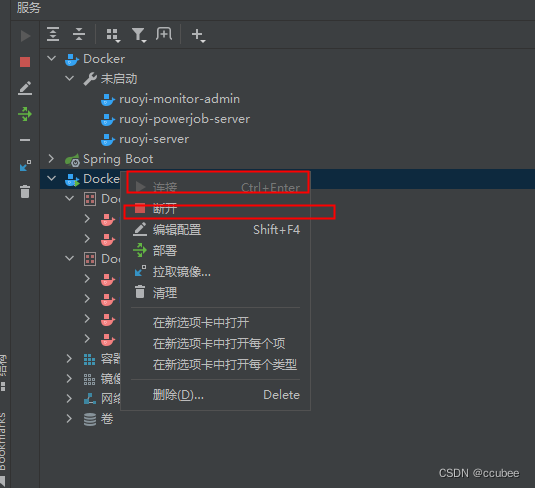
注意 构建镜像时 先查看 端口有没有被占用,占用的修改掉。
部署完发现 nginx 无法在外网访问, 查看 是否开启了防火墙,将端口开放
查看 防火墙是否开启
systemctl status firewalld
放行 nginx端口
firewall-cmd --add-port=2122/tcp --permanent
重启防火墙才会生效
firewall-cmd --reload