数据结构与算法介绍

news2024/9/22 5:40:55

什么是数据结构

定义：

数据结构就是研究数据的存储方式；数据存储的目的是方便后期对数据的再利用；选择合适的方式来存储数据，是数据结构的核心内容。

数据存储结构的选择：取决于两方面，即数据的逻辑结构和存储结构（又称物理结构）

1. 逻辑结构：数据元素之间的逻辑关系，是从具体的问题抽象出来的数据模型。

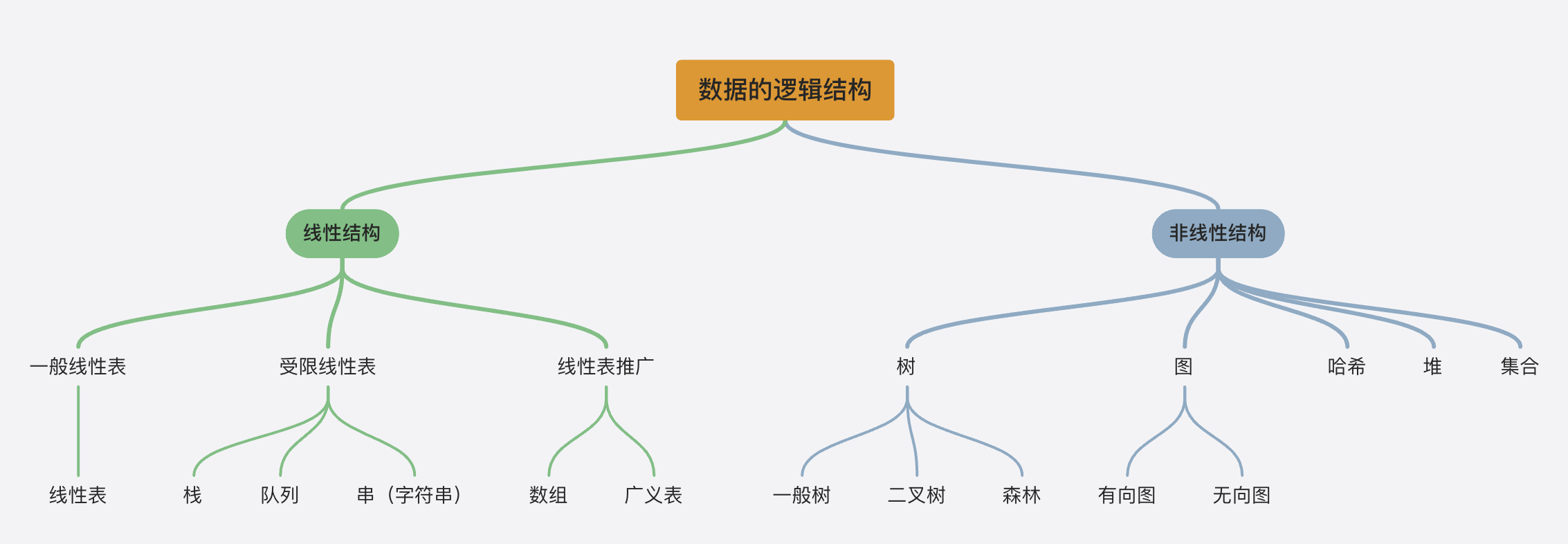
线性结构：结构中的元素只存在一对一的关系。

非线性结构：结构中的元素存在非一对一的关系，包括一对多、多对多、集合。

2. 存储结构（物理结构）：数据的逻辑结构在计算机内存中的存储方式称为数据的物理结构，也称为存储结构。

数据结构的几种存储结构：

线性表，细分为顺序表、链表、栈、队列；
数结构，包括普通树、二叉树、线性二叉树等；
图存储结构

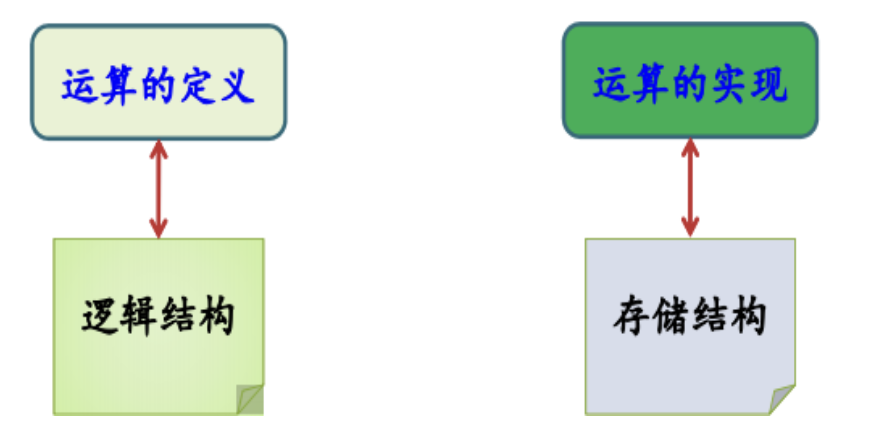
逻辑结构、存储结构和运算三者之间的关系：

数据类型：

是高级程序设计语言中的一个基本概念，在计算机科学和计算机编程中，数据类型或简单的类型是数据的一个属性，它告诉编译器或解释器程序员打算如何使用数据。大多数编程语言支持整数（大小不同）、浮点数（近似实数）、字符和布尔值的基本数据类型。

数据类型约束表达式的值，例如变量或函数，可能需要。此数据类型定义了可以对数据执行的操作、数据的含义以及存储该类型值的方式。

数据类型提供一组值，表达式（即变量、函数等）可以从中获取其值。

什么是算法

定义：

数学和逻辑的角度，算法本质上是一种逻辑关系的推理，面向现实问题的时候就要选择一套比较符合现象描述的逻辑关系。

计算机的角度，算法通常指由计算机执行的一系列指令，即所谓的程序，有明确的输入和输出，用于解决输入给计算机的问题，计算机中的算法表述方式有自然语言、伪代码、程序语言等。

算法的五个特性：

输入 —— 一个算法应以待解决的问题的信息作为输入
输出 —— 输入对应指令集处理后得到的信息
可行性 —— 算法是可行的，即算法中的每一条指令都是可以实现的，均能在有限的时间内完成
有穷性 —— 算法执行的指令个数是有限的，每个指令又是在有限时间内完成的，因此整个算法也是在有限时间内可以结束
确定性 —— 算法对于特定的合法输入，其对应的输出是唯一的；即当算法从一个特定输入开始，多次执行同一指令集结果总是相同的

算法性能分析：

一般用复杂度来分析算法性能，复杂度即通过事先估算法计算出的用来衡量算法效率的值。因此并不是说代码的长度越长复杂度就越高，或者代码中的数据越多复杂度就越高。

1. 时间复杂度——用来衡量算法消耗时间的多少

用函数来定性描述该算法的运行时间

假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这称作为算法的渐近时间复杂度，简称时间复杂度，记为 O(f(n))。

【大 O表示法：】

大 O 用来表示上界的，当用他作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界；
决定使用哪些算法，不是时间复杂度越低越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适（在有常数项的时候）。

[1.] 为什么在计算时间复杂度的时候要忽略常数项系数呢？

因为根据大O的定义，大 O 就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度，这个数据量也就是常数项系数已经不起决定性作用的数据量；

但当常数项很大的时候，也需要考虑；

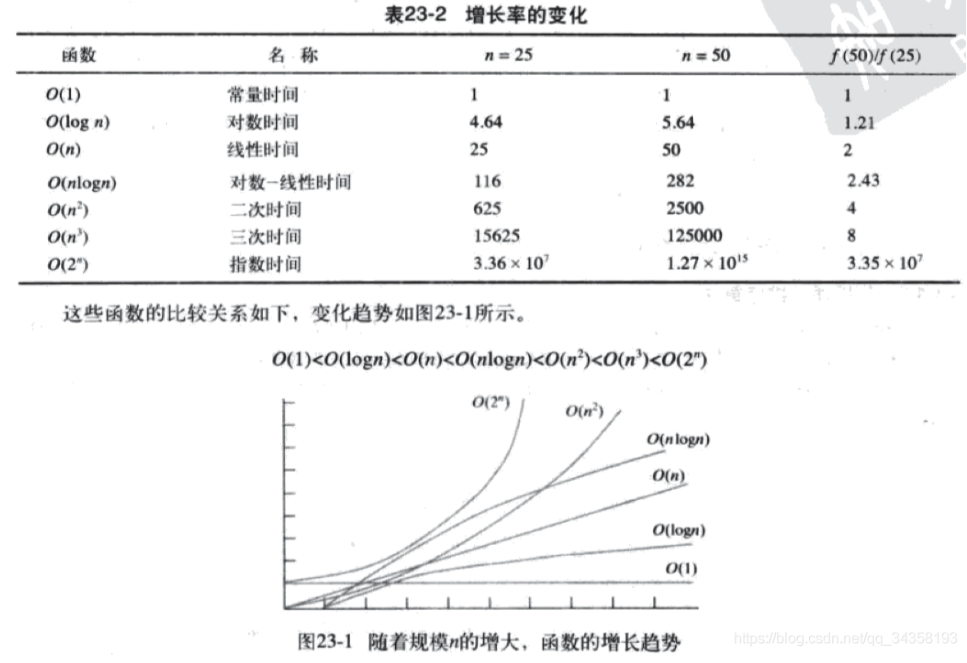
【算法时间复杂度排序：】

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(nlogn)线性对数阶 < O(n^2)平方阶 < O(n^3)立方阶 < O(2^n)指数阶
复杂表达式化简：去加法常数项--->去常数系数--->保留最高项--->去掉数量级小的项；
O(logn)中的 log 是以什么为底：一般忽略底数的描述；

[2.] 如何计算时间复杂度：主要看执行的次数和输入的关系

[3.]常见算法复杂度介绍：

常数阶：O(1)
- 是最低的时空复杂度，也就是耗时/耗空间与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变
- 哈希算法就是典型的 O(1)的时间复杂度
- 只要循环次数已知，为常数且与传参数无关，其时间复杂度即为 O(1)
- 一般而言，不论代码有多少行，只有其中没有循环、递归，则其复杂度都是 O(1)
对数阶：log(n)
- 当数据增大 n 倍时，耗时增大 logn 倍数，比如当数据增大 256 倍时，耗时只增大 8 倍，是比线性还要低的时间复杂度；
- 二分查找、幂运算、欧几里得算法都是的log(n)时间复杂度

int cnt = 1;
while (cnt < n)
{
    cnt *= 2;
}
//由于 cnt 每次乘以 2 之后都会更加逼近n，在有 x 次数之后，cnt 将会大于 n 从而跳出循环，所以有 2^x = n,
//也就是 x=log2n，所以这个循环的时间复杂度为 O(logn).

线性阶：输入和输入成正比，O(n)
- 计数排序、基数排序、桶排序的时间复杂度都是 O(n)；

 
for(int i=0;i<n;i++){
	sum += i;
} 
//当n=1，执行一次，当n=100，执行100次 ，所以当为n时，执行n次，所以时间复杂度为O(n)

线性对数阶：O(nlog(n))

int n =100;
int m = 1024;
for(int i=0; i<n; i++){
    while(i < m){
        i = i*2;
    }
}
// while循环是一个对数阶为log1024 记做logn,
//for循环是一个线性阶n, n=100, 则他们一起的时间复杂度为O(nlogn)

平方阶：输入和输入成平方，O(n^2)

for(int i=0;i<n;i++){
   for(int j=0;j<n;j++){
       
    }
}
//两层 for 循环，每层都执行 n 次，所以时间复杂度是 O(n^2)

立方阶：O(n^3)
- 三层循环嵌套
指数阶：O(2^n)
- 斐波那契算法

long function(int n) {    
    if (n <= 1) {        
        return 1;
    } else {        
        return function(n - 1) + function(n - 2);
    }
}//斐波那契算法

2. 空间复杂度——用来衡量算法所需要开辟新空间的多少