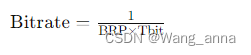16.cal指令

cal命令可以用来显示公历（阳历）日历。公历是现在国际通用的历法，又称格列历，通称阳历。“阳历”又名“太阳历”，系以地球绕行太阳一周为一年，为西方各国所通用，故又名“西历”。

命令格式： cal [参数][月份][年份]
功能： 用于查看日历等时间信息，如只有一个参数，则表示年份(1-9999)，如有两个参数，则表示月份和年份

常用选项：

        -3 显示系统前一个月，当前月，下一个月的月历
        -j  显示在当年中的第几天（一年日期按天算，从1月1号算起，默认显示当前月在一年中的天数）
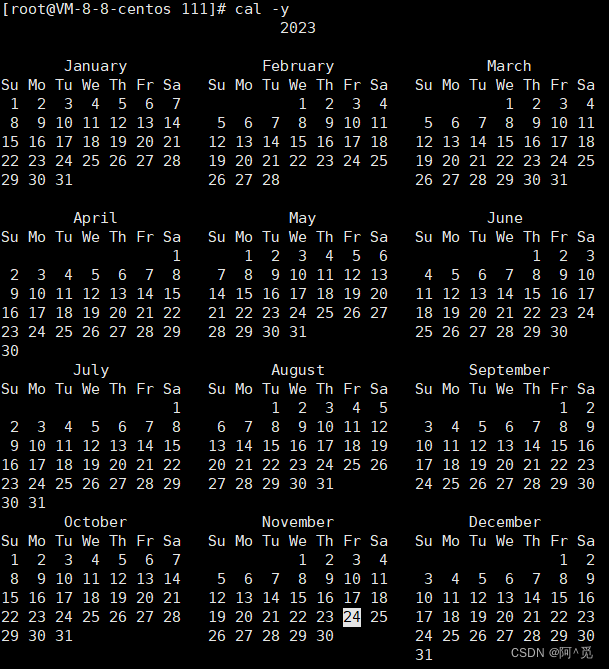
        -y  显示当前年份的日历

举例：

当年日历：

2018的日历：

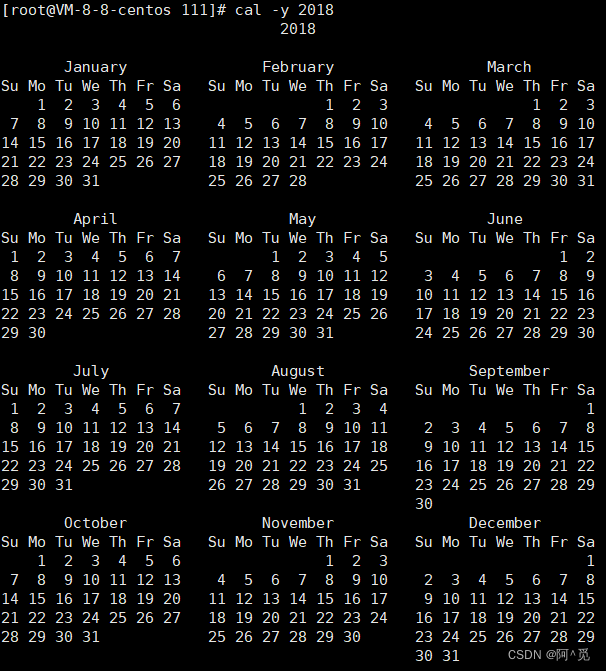
前先后三个月的日历：

17.find指令：（很重要） -name

Linux下find命令在目录结构中搜索文件，并执行指定的操作。
Linux下find命令提供了相当多的查找条件，功能很强大。由于find具有强大的功能，所以它的选项也很多，其中大部分选项都值得我们花时间来了解一下。
即使系统中含有网络文件系统( NFS)，find命令在该文件系统中同样有效，只你具有相应的权限。
在运行一个非常消耗资源的find命令时，很多人都倾向于把它放在后台执行，因为遍历一个大的文件系统可能会花费很长的时间(这里是指30G字节以上的文件系统)。

语法： find pathname -options
功能： 用于在文件树种查找文件，并作出相应的处理（可能访问磁盘）

常用选项：

        -name 按照文件名查找文件。

这个表示从 / （根目录）下按照文件名查找名为test.c的文件

18.grep指令

参考文档（grep）

语法： grep [选项] 搜寻字符串 文件
功能： 在文件中搜索字符串，将找到的行打印出来

常用选项：

        -i ：忽略大小写的不同，所以大小写视为相同
        -n ：顺便输出行号
        -v ：反向选择，亦即显示出没有 '搜寻字符串' 内容的那一行

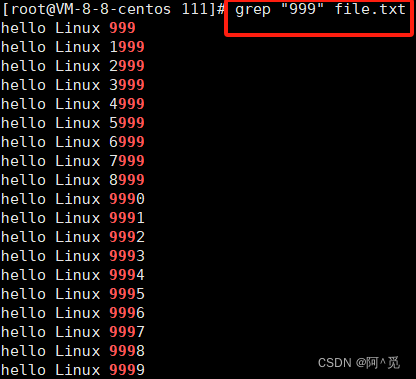
找到文件中包含字符999的所有内容：

忽略大小写：

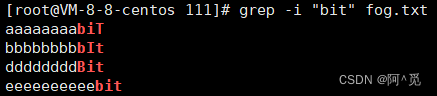
顺便输出行号：

反向打印：

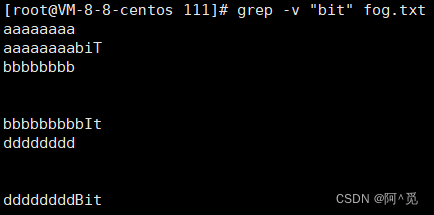
结合：

19.zip/unzip

语法： zip 压缩文件.zip 目录或文件
功能： 将目录或文件压缩成zip格式

常用选项：

        -r 递 归处理，将指定目录下的所有文件和子目录一并处理

举例：

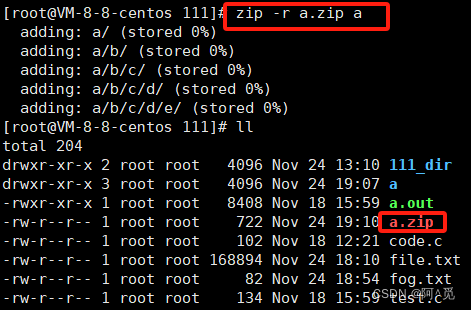
zip -r xxx.zip 要压缩的目录（递归压缩）

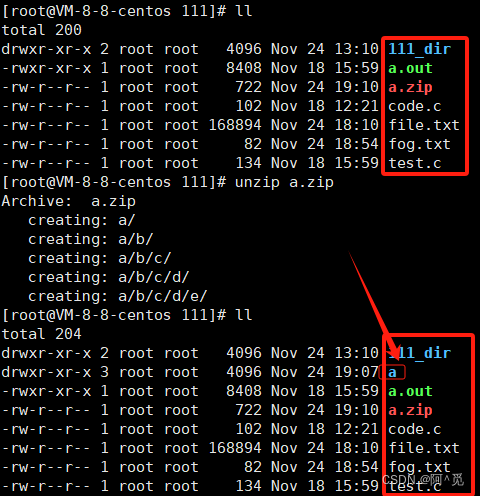
unzip xxx.zip（解压缩）