【机器学习】聚类（一）：原型聚类：K-means聚类

文章目录

一、实验介绍
- 1. 算法流程
- 2. 算法解释
- 3. 算法特点
- 4. 应用场景
- 5. 注意事项
二、实验环境
- 1. 配置虚拟环境
- 2. 库版本介绍
三、实验内容
- 0. 导入必要的库
- 1. Kmeans类
- - a. 构造函数
  - b. 闵可夫斯基距离
  - c. 初始化簇心
  - d. K-means聚类
  - e. 聚类结果可视化
- 2. 辅助函数
- 3. 主函数
- - a. 命令行界面（CLI）
  - b. 数据加载
  - c. 模型训练及可视化
- 4. 运行脚本的命令
- 5. 代码整合

原型聚类中的K均值算法是一种常用的聚类方法，该算法的目标是通过迭代过程找到数据集的簇划分，使得每个簇内的样本与簇内均值的平方误差最小化。这一过程通过不断迭代更新簇的均值来实现。

一、实验介绍

在这里插入图片描述

1. 算法流程

初始化： 从样本集中随机选择k个样本作为初始均值向量。
迭代过程： 重复以下步骤直至均值向量不再更新：
- 对每个样本计算与各均值向量的距离。
- 将样本划分到距离最近的均值向量所对应的簇。
- 更新每个簇的均值向量为该簇内样本的平均值。
输出： 返回最终的簇划分。

2. 算法解释

步骤1中，通过随机选择初始化k个均值向量。
步骤2中，通过计算样本与均值向量的距离，将每个样本分配到最近的簇。然后，更新每个簇的均值向量为该簇内样本的平均值。
算法通过迭代更新，不断优化簇内样本与均值向量的相似度，最终得到较好的聚类结果。

3. 算法特点

K均值算法是一种贪心算法，通过局部最优解逐步逼近全局最优解。
由于需要对每个样本与均值向量的距离进行计算，算法复杂度较高。
对于大型数据集和高维数据，K均值算法的效果可能受到影响。

4. 应用场景

K均值算法适用于样本集可以被均值向量较好表示的情况，特别是当簇呈现球形或近似球形分布时效果较好。
在图像分割、用户行为分析等领域广泛应用。

5. 注意事项

对于K均值算法，初始均值向量的选择可能影响最终聚类结果，因此有时需要多次运行算法，选择最优的结果。
算法对异常值敏感，可能导致簇的均值向量被拉向异常值，因此在处理异常值时需要谨慎。

二、实验环境

1. 配置虚拟环境

conda create -n ML python==3.9

conda activate ML

conda install scikit-learn matplotlib seaborn

2. 库版本介绍

软件包	本实验版本
matplotlib	3.5.2
numpy	1.21.5
python	3.9.13
scikit-learn	1.0.2
seaborn	0.11.2

三、实验内容

0. 导入必要的库

import numpy as np
import random
import seaborn as sns
import matplotlib.pyplot as plt
import argparse

1. Kmeans类

__init__ ：初始化K均值聚类的参数，包括聚类数目 k、数据 data、初始化模式 mode（默认为 “random”）、最大迭代次数 max_iters、闵可夫斯基距离的阶数 p、随机种子 seed等。
minkowski_distance 函数：计算两个样本点之间的闵可夫斯基距离。
center_init 函数：根据指定的模式初始化聚类中心。
fit 方法：执行K均值聚类的迭代过程，包括分配样本到最近的簇、更新簇中心，直到满足停止条件。
visualization 函数：使用Seaborn和Matplotlib可视化聚类结果。

a. 构造函数

class Kmeans(object):
    def __init__(self, k, data: np.ndarray, mode="random", max_iters=0, p=2, seed=0):
        self.k = k
        self.data = data

        self.mode = mode
        self.max_iter = max_iters if max_iters > 0 else int(1e8)
        self.p = p
        self.seed = seed

        self.centers = None
        self.clu_idx = np.zeros(len(self.data), dtype=np.int32)  # 样本的分类簇
        self.clu_dist = np.zeros(len(self.data), dtype=np.float64)  # 样本与簇心的距离

参数：
- 聚类数目 k
- 数据集 data
- 初始化模式 mode
- 最大迭代次数 max_iters
- 闵可夫斯基距离的阶数 p 以及随机种子 seed。
初始化类的上述属性，此外
- self.centers 被初始化为 None，表示簇心尚未计算
- self.clu_idx 和 self.clu_dist 被初始化为全零数组，表示每个样本的分类簇和与簇心的距离。

b. 闵可夫斯基距离

    def minkowski_distance(self, x, y=0):
        return np.linalg.norm(x - y, ord=self.p)

使用了NumPy的 linalg.norm 函数，其中 ord 参数用于指定距离的阶数。

c. 初始化簇心

    def center_init(self):
        random.seed(self.seed)

        if self.mode == "random":
            ids = random.sample(range(len(self.data)), k=self.k)  # 随机抽取k个样本下标
            self.centers = self.data[ids]  # 选取k个样本作为簇中心
        else:
            ids = [random.randint(0, self.data.shape[0])]
            for _ in range(1, self.k):
                max_idx = 0
                max_dis = 0
                for i, x in enumerate(self.data):
                    if i in ids:
                        continue
                    dis = 0
                    for y in self.data[ids]:
                        dis += self.minkowski_distance(x - y)
                    if max_dis < dis:
                        max_dis = dis
                        max_idx = i
                ids.append(max_idx)
            self.centers = self.data[ids]

根据指定的初始化模式，选择随机样本或使用 “far” 模式。
- 在 “random” 模式下，通过随机抽样选择 k 个样本作为簇心；
- 在 “far” 模式下，通过计算每个样本到已选簇心的距离之和，选择距离总和最大的样本作为下一个簇心。

d. K-means聚类

    def fit(self):
        self.center_init()  # 簇心初始化

        for _ in range(self.max_iter):
            flag = False  # 判断是否有样本被重新分类

            # 遍历每个样本
            for i, x in enumerate(self.data):
                min_idx = -1  # 最近簇心下标
                min_dist = np.inf  # 最小距离
                for j, y in enumerate(self.centers):  # 遍历每个簇，计算与该样本的距离
                    # 计算样本i到簇j的距离dist

                    dist = self.minkowski_distance(x, y)

                    if min_dist > dist:
                        min_dist = dist
                        min_idx = j
                if self.clu_idx[i] != min_idx:
                    # 有样本改变分类簇，需要继续迭代更新簇心

                    flag = True

                # 记录样本i与簇的最小距离min_dist，及对应簇的下标min_idx
                self.clu_idx[i] = min_idx
                self.clu_dist[i] = min_dist

            # 样本的簇划分好之后，用样本均值更新簇心
            for i in range(self.k):
                x = self.data[self.clu_idx == i]
                # 用样本均值更新簇心
                self.centers[i] = np.mean(x, axis=0)

            if not flag:
                break

在每次迭代中
- 遍历每个样本，计算其到各个簇心的距离，将样本分配到距离最近的簇中。
- 更新每个簇的均值（簇心）为该簇内所有样本的平均值。
上述过程迭代进行，直到满足停止条件（样本不再重新分配到不同的簇）或达到最大迭代次数。

e. 聚类结果可视化

    def visualization(self, k=3):
        current_palette = sns.color_palette()
        sns.set_theme(context="talk", palette=current_palette)
        for i in range(self.k):
            x = self.data[self.clu_idx == i]
            sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8)
        sns.scatterplot(x=self.centers[:, 0], y=self.centers[:, 1], marker="+", s=500)
        plt.title("k=" + str(k))
        plt.show()

2. 辅助函数

def order_type(v: str):
    if v.lower() in ("-inf", "inf"):
        return -np.inf if v.startswith("-") else np.inf
    else:
        try:
            return float(v)
        except ValueError:
            raise argparse.ArgumentTypeError("Unsupported value encountered")


def mode_type(v: str):
    if v.lower() in ("random", "far"):
        return v.lower()
    else:
        raise argparse.ArgumentTypeError("Unsupported value encountered")

order_type 函数：用于处理命令行参数中的 -p（距离测量参数），将字符串转换为浮点数。
mode_type 函数：用于处理命令行参数中的 --mode（初始化模式参数），将字符串转换为合法的初始化模式。

3. 主函数

a. 命令行界面（CLI）

使用 argparse 解析命令行参数

    parser = argparse.ArgumentParser(description="Kmeans Demo")
    parser.add_argument("-k", type=int, default=3, help="The number of clusters")
    parser.add_argument("--mode", type=mode_type, default="random", help="Initial centroid selection")
    parser.add_argument("-m", "--max-iters", type=int, default=40, help="Maximum iterations")
    parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")
    parser.add_argument("--seed", type=int, default=0, help="Random seed")
    parser.add_argument("--dataset", type=str, default="./kmeans.2.txt", help="Path to dataset")
    args = parser.parse_args()

b. 数据加载

从指定路径加载数据集。

	dataset = np.loadtxt(args.dataset)

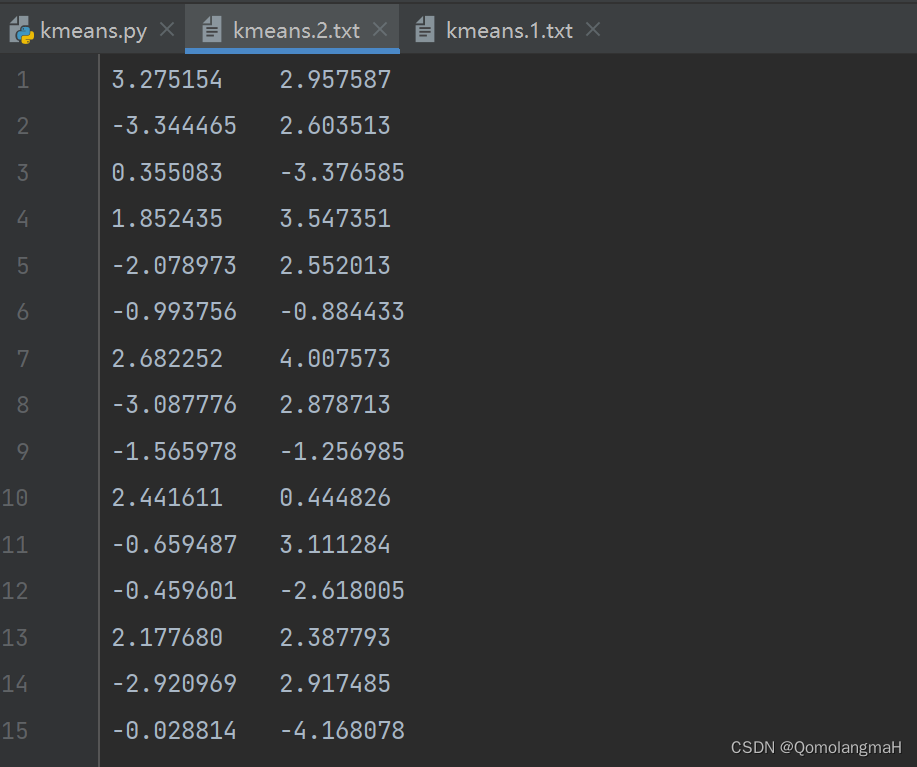
在这里插入图片描述

c. 模型训练及可视化

	model = Kmeans(k=args.k, data=dataset, mode=args.mode, max_iters=args.max_iters, p=args.p,
                   seed=args.seed)
    model.fit()

    # 聚类结果可视化
    model.visualization(k=args.k)

4. 运行脚本的命令

通过命令行传递参数来运行脚本，指定聚类数目、初始化模式、最大迭代次数等。

python kmeans.py -k 3 --mode random -m 40 -p 2 --seed 0 --dataset ./kmeans.2.txt

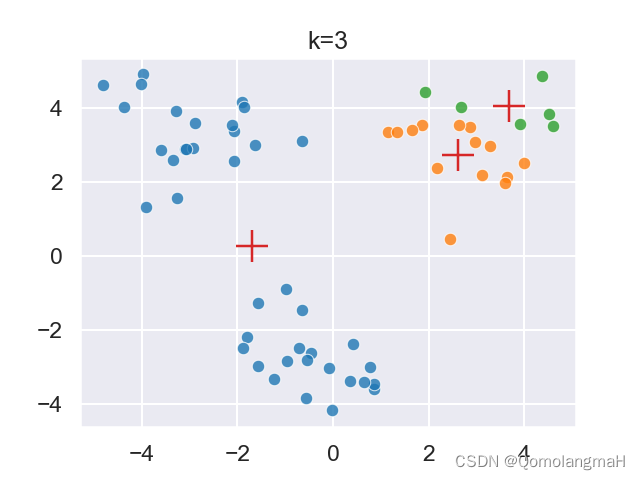
在这里插入图片描述

5. 代码整合

import numpy as np
import random
import seaborn as sns
import matplotlib.pyplot as plt
import argparse


class Kmeans(object):
    def __init__(self, k, data: np.ndarray, mode="random", max_iters=0, p=2, seed=0):
        self.k = k
        self.data = data

        self.mode = mode
        self.max_iter = max_iters if max_iters > 0 else int(1e8)
        self.p = p
        self.seed = seed

        self.centers = None
        self.clu_idx = np.zeros(len(self.data), dtype=np.int32)  # 样本的分类簇
        self.clu_dist = np.zeros(len(self.data), dtype=np.float64)  # 样本与簇心的距离

    def minkowski_distance(self, x, y=0):

        return np.linalg.norm(x - y, ord=self.p)

    # 簇心初始化
    def center_init(self):
        random.seed(self.seed)

        if self.mode == "random":
            ids = random.sample(range(len(self.data)), k=self.k)  # 随机抽取k个样本下标
            self.centers = self.data[ids]  # 选取k个样本作为簇中心
        else:
            ids = [random.randint(0, self.data.shape[0])]
            for _ in range(1, self.k):
                max_idx = 0
                max_dis = 0
                for i, x in enumerate(self.data):
                    if i in ids:
                        continue
                    dis = 0
                    for y in self.data[ids]:
                        dis += self.minkowski_distance(x - y)
                    if max_dis < dis:
                        max_dis = dis
                        max_idx = i
                ids.append(max_idx)
            self.centers = self.data[ids]

    def fit(self):
        self.center_init()  # 簇心初始化

        for _ in range(self.max_iter):
            flag = False  # 判断是否有样本被重新分类

            # 遍历每个样本
            for i, x in enumerate(self.data):
                min_idx = -1  # 最近簇心下标
                min_dist = np.inf  # 最小距离
                for j, y in enumerate(self.centers):  # 遍历每个簇，计算与该样本的距离
                    # 计算样本i到簇j的距离dist

                    dist = self.minkowski_distance(x, y)

                    if min_dist > dist:
                        min_dist = dist
                        min_idx = j
                if self.clu_idx[i] != min_idx:
                    # 有样本改变分类簇，需要继续迭代更新簇心

                    flag = True

                # 记录样本i与簇的最小距离min_dist，及对应簇的下标min_idx
                self.clu_idx[i] = min_idx
                self.clu_dist[i] = min_dist

            # 样本的簇划分好之后，用样本均值更新簇心
            for i in range(self.k):
                x = self.data[self.clu_idx == i]
                # 用样本均值更新簇心
                self.centers[i] = np.mean(x, axis=0)

            if not flag:
                break

    def visualization(self, k=3):
        current_palette = sns.color_palette()
        sns.set_theme(context="talk", palette=current_palette)
        for i in range(self.k):
            x = self.data[self.clu_idx == i]
            sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8)
        sns.scatterplot(x=self.centers[:, 0], y=self.centers[:, 1], marker="+", s=500)
        plt.title("k=" + str(k))
        plt.show()


def order_type(v: str):
    if v.lower() in ("-inf", "inf"):
        return -np.inf if v.startswith("-") else np.inf
    else:
        try:
            return float(v)
        except ValueError:
            raise argparse.ArgumentTypeError("Unsupported value encountered")


def mode_type(v: str):
    if v.lower() in ("random", "far"):
        return v.lower()
    else:
        raise argparse.ArgumentTypeError("Unsupported value encountered")


if __name__ == '__main__':
    parser = argparse.ArgumentParser(description="Kmeans Demo")
    parser.add_argument("-k", type=int, default=3, help="The number of clusters")
    parser.add_argument("--mode", type=mode_type, default="random", help="Initial centroid selection")
    parser.add_argument("-m", "--max-iters", type=int, default=40, help="Maximum iterations")
    parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")
    parser.add_argument("--seed", type=int, default=0, help="Random seed")
    parser.add_argument("--dataset", type=str, default="./kmeans.2.txt", help="Path to dataset")
    args = parser.parse_args()

    dataset = np.loadtxt(args.dataset)
    model = Kmeans(k=args.k, data=dataset, mode=args.mode, max_iters=args.max_iters, p=args.p,
                   seed=args.seed)  # args.seed)
    model.fit()

    # 聚类结果可视化
    model.visualization(k=args.k)