一、审题

题目描述

给定两个大小分别为 $m$ 和 $n$ 的正序（从小到大）数组 $nums1$ 和 $nums2$。请你找出并返回这两个正序数组的中位数。
算法的时间复杂度应该为 $O(log(m+n))$ 。

示例 1

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

信息

通过次数
$1M$
提交次数
$2.5M$
通过率
$41.8\%$

二、思路

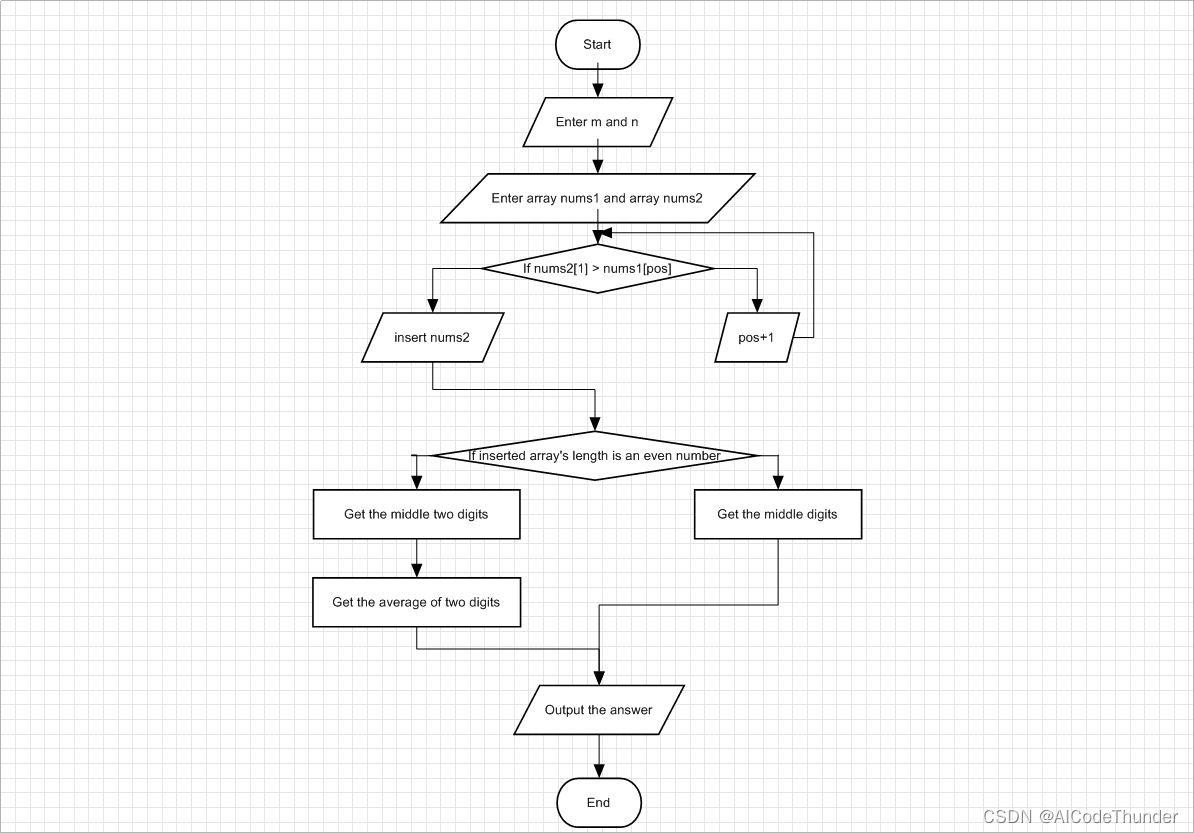
1. 分析流程

2. 尝试代码

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        if (m > n) {  // 确保 m <= n
            return findMedianSortedArrays(nums2, nums1);
        }
        int iMin = 0, iMax = m;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / 2;
            int j = (m + n + 1) / 2 - i;
            if (j != 0 && i != m && nums2[j - 1] > nums1[i]) {
                iMin = i + 1; // i 太小了，需要右移
            } else if (i != 0 && j != n && nums1[i - 1] > nums2[j]) {
                iMax = i - 1; // i 太大了，需要左移
            } else { // 此时 i 是我们需要的
                int maxLeft;  // maxLeft 表示左半部分的最大值
                if (i == 0) {
                    maxLeft = nums2[j - 1];
                } else if (j == 0) {
                    maxLeft = nums1[i - 1];
                } else {
                    maxLeft = max(nums1[i - 1], nums2[j - 1]);
                }
                if ((m + n) % 2 == 1) {  // 如果是奇数，中位数就是左半部分的最大值
                    return maxLeft;
                }

                int minRight;  // minRight 表示右半部分的最小值
                if (i == m) {
                    minRight = nums2[j];
                } else if (j == n) {
                    minRight = nums1[i];
                } else {
                    minRight = min(nums2[j], nums1[i]);
                }

                return (maxLeft + minRight) / 2.0;  // 如果是偶数，就是左半部分的最大值和右半部分的最小值的均值
            }
        }
        return 0.0;
    }
};