目录
图像感知与获取
韦伯定理
马赫带效应
图像获取
图像的采样和量化
图像内插(重采样)
图像的表示与描述
像素间的关系
exercise:4-邻域连通区域标记
本文章讲解数字图像处理的基础,大部分内容来源于课堂笔记中
图像感知与获取
人眼解剖图

屈光系统:光线由一种介质进入另一种不同折射率的介质时,会发生前进方向的改变,在眼光学中成“屈光”,屈光系统由角膜、房水、晶状体、玻璃体构成
感光系统:视网膜
视觉形成过程:物体(发射,反射)--->人眼屈光媒质--->感光细胞(视锥细胞、视杆细胞)--->感光细胞外节的光敏色素吸收光子后分解放出的能量形成膜电位发出信号--->通过突触传递给双极细胞和水平细胞,它们将信号作进一步处理后,传递给神经节细胞---->大脑皮层--->识别并产生视觉
视杆细胞:视网膜表面,负责黑白视觉,对光线的敏感程度非常敏感,主要用于暗视觉,左右人的夜视能力;对色彩没有感觉
视锥细胞:视网膜中央凹中间部分,对颜色高度敏感,具有三种类型:红色、绿色、蓝色感光细胞。常见色盲原因:其中一种视锥细胞发育出现问题
人眼聚焦:睫状体中的纤维根据目标远近,会压扁或加厚晶状体,从而改变焦距
韦伯定理
韦伯定理指出:差别阈限和标准刺激的强度成正比,并且差别阈限和标准刺激的比例是一个常数
以视觉为例,如果你在一个相对暗的房间中看到了两个光源,其中一个比另一个更亮,那么你可能会轻松地注意到它们之间的差别。但如果你在一个非常明亮的环境中,两个光源的强度差异需要更大才能被感知到相同的程度。这就是韦伯定律的体现:感知到的差别阈限与刺激强度成比例
然而,对于不同的感知系统、不同的感官以及不同的实验条件,韦伯比可能会略有变化。韦伯比大说明感知系统相对较不敏感,需要更大的刺激变化才能产生可察觉的差异。相反,韦伯比小说明感知系统相对较敏感,较小的刺激变化就足以引起可察觉的差异
马赫带效应
马赫带是一种主观的边缘对比效应。当观察两块亮度不同的区域时,边界处亮度对比加强,使轮廓表现得特别明显

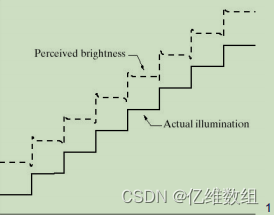
马赫带效应的出现是人类的视觉系统造成的。生理学对马赫带效应的解释是:人类的视觉系统有增强边缘对比度的机制
图像获取
图像获取指的是将物体成像的过程,由“照射”源和形成图像的“场景”元素对光能的反射或吸收而产生的
图像获取主要有三种方式:使用单个传感器获取图像、使用条带传感器获取图像、使用传感器阵列获取图像
阵列传感器CCD

图像的采样和量化
图像采样是指从连续的图像中获取离散的样本或数据点的过程。想象一张图像是由无数个像素组成的,像素是图像中最小的单元。采样即是在图像中选取部分像素以表示整个图像。采样过程决定了图像的分辨率。高分辨率图像具有更多的像素,可以呈现更多的细节;低分辨率图像则只包含少量像素,细节较少

图像量化是指将采样得到的图像数据转换为离散的数值表示的过程。数字图像中的每个像素需要用数字来表示。这个过程就是量化。常见的是将图像的亮度范围映射为数字值。例如,如果是灰度图像,可能使用 0 到 255 之间的整数来表示像素的灰度级别。0代表黑色,255代表白色

通俗地说,采样就像是用相机拍照,而量化则是将照片上的颜色和亮度转换成数字。采样决定了图像的清晰度和细节程度,量化则决定了图像的色彩和亮度等方面的表现
动态范围:描述了一张图片中最暗的地方到最亮的地方的亮度差异。想象一下你站在一个夏日的海滩上,太阳光照在沙滩上,海水里可能有一些阴影。动态范围就是指能在同一张照片中捕捉到这个阳光下明亮的沙滩和海水中较暗的阴影的能力
比如8比特的灰度图像,下述k=8

饱和度:图像中颜色的强度或纯度。高饱和度表示颜色非常鲜艳、明亮,而低饱和度则使颜色看起来更灰淡或淡淡的。想象一下一个色彩斑斓的花园照片,高饱和度可能使得花朵的颜色非常生动,而低饱和度则可能导致花色看起来更为柔和和淡雅
对比度:图像中亮和暗之间的差异程度。高对比度的图像中,明暗之间的差异非常明显,而低对比度的图像则使得明暗过渡更为平缓。想象一下一张黑白照片,高对比度可能导致清晰的黑白分界线,而低对比度则可能使得灰度变化更为平缓
均匀量化:将数据范围均匀地划分为若干个区间,然后将每个区间映射到一个离散值
非均匀量化:可以根据数据的分布情况不均匀地划分区间。这样可以更灵活地对图像进行量化,使得对图像中某些区域的细节更加敏感
空间分辨率:是指遥感图像上能够详细区分的最小单元的尺寸或大小,是用来表征影像分辨地面目标细节的指标
灰度分辨率:涉及到图像中可见的不同灰度层次或颜色层次的数量,比如8位灰度深度意味着256个不同的灰度级别

图像内插(重采样)
下采样/缩小图片:行列删除
上采样/放大图片:创建新的像素位置,对新位置上的像素赋值
针对图像内插,下面介绍三种不同的插值方法:
最近邻插值:把原图中最近邻的灰度赋给每个新像素
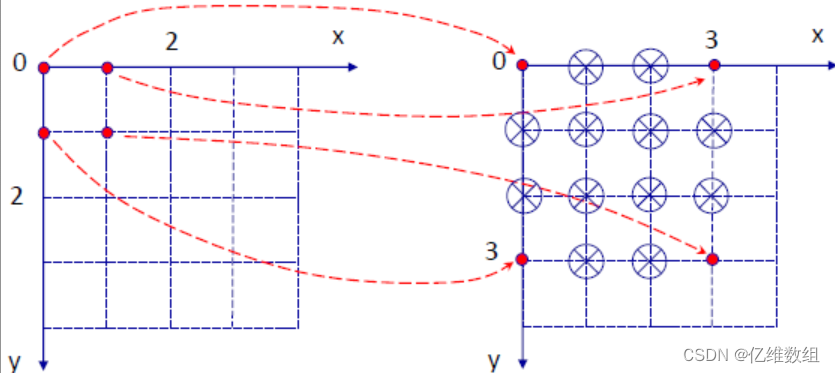
这种方法的优缺点很明显,优点就是实现简单、速度快,缺点就是容易产生马赛克效应
双线性插值:其核心思想是在两个方向分别进行一次线性插值


大致原理:分别在Q12Q22、Q11Q21的连线上,通过最邻近插值按比例算出R2、R1的f值,然后再在R1R2的连线上同理算出P的f值
优点: 比最近邻插值效果好,没有明显的块效应
缺点: 计算量比最近邻插值大,使图像细节退化
双三次插值使用16个邻近像素的灰度值进行插值计算,采用二次多项式的插值方法。这样可以更好地保留图像的细节,并减少缩放操作引入的伪影和失真

图像的表示与描述
图像一般用二维矩阵表示,矩阵元素 f (m, n)表示图像在第 m 行 第 n 列的像素值,称为像素

坐标索引
为了编程方便起见,在图像的描述中,我们以矩阵坐标系来定义图像的坐标
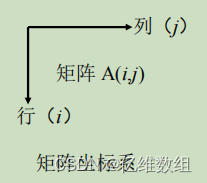
对于灰度图像,图像中每个像素信息由一个量化的灰度级描述,没有色彩信息,灰度图像的灰度级常为8bits,即0--255,0位纯黑,255位纯白
还有一种图像叫做二值图像或者是黑白图像,其只有两种像素值,要么纯黑,要么纯白

可以通过对灰度图像二值化变成黑白图像,变成黑白图像的图片,可通过分析图像连通区域估计一些东西的数量(比如统计下面米粒的数量)

像素间的关系
像素与像素之间的关系:
邻接:通常,如果像素在水平、垂直或对角线方向上相邻叫邻接
连接:通常指的是一组相邻的像素,它们在某种意义上被视为一个整体
连通:一组像素被称为连通,如果在这组像素之间存在一条路径,使得路径上的相邻像素之间也是相邻的。连通性通常用于描述图像中区域的完整性
通路:指的是连接两个像素的路径,这个路径可以通过相邻的像素进行跳跃,也可以是一条像素的序列
像素与集合之间也有上述的邻接、连接、连通关系
像素间的距离有多种定义:
欧式距离DE

曼哈顿距离D4(城区距离)
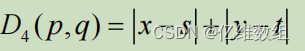
切比雪夫距离D8(棋盘格距离)
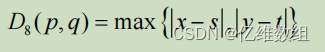
4-邻域(N4(p)) p为像素点的名称

对角邻域/D-邻域(ND(p))

8-邻域(N8(p)):为4-邻域和D-邻域的相加
令V是用于定义邻接的灰度值集合
4-邻接:q在p的4-邻域N4(p)中,且它们都在V中取值,q在N4(p)中意味着p也在N4(q)中
8-邻接:同上,只不过是8-邻域
m-邻接/混合邻接:
1.两个像素p和q在V中取值
2.满足下列条件之一:
•q在N4(p)中,即两个像素p和q是4-邻接;
•q在ND(p)中,且N4(p)和N4(q)在V的意义下是空集,即N4(p)∩N4(r)不包含V中取值的像素

像素间的通路:是指连接两个像素的路径,这个路径可以通过相邻的像素进行跳跃,也可以是一条像素的序列,根据邻接方式不同有4-通路和8-通路
像素间的连通:S表示图像中像素一个子集,如果S中的两个像素p、q之间存在一个完全由S中像素组成的通路,则p和q在S中是连通的,也分为4-连通和8-连通
令R表示图像中像素的一个子集。若R是一个连通集,称R为图像的一个区域
若 Ri和 Rj形成一个连通集时,称 Ri和 Rj为邻接区域
边界:也称为区域的轮廓,是该区域的一个子集,但在其邻域中有不属于该区域的像素,它将该区域与其他区域分开。必须指定所用连接类型才能确定一个像素是否属于边界
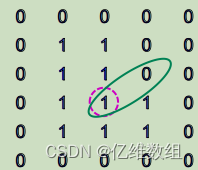
比如,上图,如果定义连接类型为8-连接则圈住的1为于赋1值区域的边界,如果定义为4-连接,那么它的4-邻域没有赋1值区域以外的像素,那么它就不是边界了
exercise:4-邻域连通区域标记
4-邻域连通区域标记是图像处理中的一项基本任务,常用于标记图像中具有相同像素值且相邻的区域。下面是一个简单的Python代码示例,使用深度优先搜索(DFS)进行4-邻域连通区域标记:
def dfs(image, row, col, label, visited, connectivity=4):
# 4-邻域的相邻像素坐标增量
neighbors = [(-1, 0), (0, -1), (0, 1), (1, 0)] if connectivity == 4 else [(-1, 0), (0, -1), (0, 1), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1)]
# 标记当前像素
image[row][col] = label
visited[row][col] = True
# 遍历相邻像素
for dr, dc in neighbors:
new_row, new_col = row + dr, col + dc
# 检查相邻像素是否在图像范围内且未被访问
if 0 <= new_row < len(image) and 0 <= new_col < len(image[0]) and not visited[new_row][new_col] and image[new_row][new_col] == 1:
dfs(image, new_row, new_col, label, visited, connectivity)
def label_connected_regions(image, connectivity=4):
rows, cols = len(image), len(image[0])
visited = [[False for _ in range(cols)] for _ in range(rows)]
label = 0
for i in range(rows):
for j in range(cols):
if not visited[i][j] and image[i][j] == 1:
label += 1
dfs(image, i, j, label, visited, connectivity)
return image
# 示例用法
image = [
[1, 0, 1, 0],
[1, 0, 1, 0],
[0, 0, 1, 1],
[1, 0, 0, 0]
]
result = label_connected_regions(image, connectivity=4)
print(result)
![]()