时间复杂度空间复杂度 ---java

一. 算法效率

二.时间复杂度

2.1 时间复杂度的概念

2.2 大O的渐进表示法

2.3常见时间复杂度计算举例

三. 空间复杂度

一. 算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率 。

时间效率被称为时间复杂度，而空间效率被称作 空间复杂度 。

时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间.

在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

二.时间复杂度

2.1 时间复杂度的概念

时间复杂度的定义：在计算机科学中， 算法的时间复杂度是一个数学函数 ，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

2.2 大O的渐进表示法

// 请计算一下 func1 基本操作执行了多少次？

void func1 ( int N ){

        int count = 0 ;

        for ( int i = 0 ; i < N ; i ++ ) { //N

                for ( int j = 0 ; j < N ; j ++ ) { //N

                        count ++ ;

                }

        }

        for ( int k = 0 ; k < 2 * N ; k ++ ) { //2*N

                count ++ ;

        }

        int M = 10 ;

        while (( M -- ) > 0 ) { //10

                count ++ ;

        }

        System . out . println ( count );

}

Func1 执行的基本操作次数：

使用大O的渐进表示法:

1 、用常数 1 取代运行时间中的所有加法常数。

2 、在修改后的运行次数函数中，只保留最高阶项。

3 、如果最高阶项存在且不是 1 ，则去除与这个项目相乘的常数。得到的结果就是大 O 阶。

使用大O的渐进表示法以后，Func1的时间复杂度为：

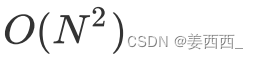
通过上面我们会发现大 O 的渐进表示法 去掉了那些对结果影响不大的项 ，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数 ( 上界 )

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数 ( 下界 )

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为 O(N).

2.3常见时间复杂度计算举例

【实例 1 】

// 计算 func2 的时间复杂度？

void func2 ( int N ) {

        int count = 0 ;

        for ( int k = 0 ; k < 2 * N ; k ++ ) { //2*N

                count ++ ;

        }

        int M = 10 ;

        while (( M -- ) > 0 ) { //10

                count ++ ;

        }

        System . out . println ( count );

}

基本操作执行了2N+10次，通过推导大O阶方法--->时间复杂度为 O(N)

【实例2】

// 计算 func3 的时间复杂度？

void func3 ( int N , int M ) {

        int count = 0 ;

        for ( int k = 0 ; k < M ; k ++ ) { //M

                count ++ ;

        }

        for ( int k = 0 ; k < N ; k ++ ) { //N

                count ++ ;

        }

        System . out . println ( count );

}

基本操作执行了M+N次，有两个未知数M和N，时间复杂度为 O(N+M)

【实例3】

// 计算 func4 的时间复杂度？

void func4 ( int N ) {

        int count = 0 ;

        for ( int k = 0 ; k < 100 ; k ++ ) { //100

                count ++ ;

        }

        System . out . println ( count );

}

基本操作执行了100次，通过推导大O阶方法，时间复杂度为 O(1).

【实例4】

// 计算 bubbleSort 的时间复杂度？

void bubbleSort ( int [] array ) {

        for ( int end = array . length ; end > 0 ; end -- ) {

                boolean sorted = true ;

                for ( int i = 1 ; i < end ; i ++ ) {

                        if ( array [ i - 1 ] > array [ i ]) {

                                Swap ( array , i - 1 , i );

                                sorted = false ;

                        }

                }

                if ( sorted == true ) {

                        break ;

                }

        }

}

错误思想: 因为是两层循环嵌套, 所以时间复杂度为O(N^2)

时间复杂度的计算是要配合逻辑的

正确解法:

第一层循环: 当end = n时, 里层 i 从1到 n-1, 循环了n-1次

第二层循环: 当end = n-1时, 里层i从1到n-2, 循环了n-2次

第三层循环: 当end = n-2时, 里层i从1到n-3,循环了n-3次

...

第n-2层循环: 当end = 3时, 里层i从1到2,循环了2次

第n-1层循环: 当end = 2时, 里层i从1到1,循环了1次

第n层循环: 当end = 1时, 里层循环不进行

所以共循环了(n-1)+(n-2)+(n-3)+...3+2+1=n*(n-1)/2, 通过推导大O阶方法, 时间复杂度为 O(N^2)

【实例5】

// 计算 binarySearch 的时间复杂度？

int binarySearch ( int [] array , int value ) {

        int begin = 0 ;

        int end = array . length - 1 ;

        while ( begin <= end ) {

                int mid = begin + (( end - begin ) / 2 );

                if ( array [ mid ] < value )

                        begin = mid + 1 ;

                else if ( array [ mid ] > value )

                        end = mid - 1 ;

                else

                        return mid ;

        }

        return - 1 ;

}

二分查找法的思路: 共N个数

第一次查找: 砍掉一半,剩下N/2个

第二次查找: 再砍掉一半, 剩下N/2^2个

第三次查找: 再砍掉一半, 剩下N/2^3个

...

第X次查找: 再砍掉一半, 剩下N/2^X个

当只剩下一个数时, 就找到了这个数, 所以N/2^X = 1 , 解得X=log(以2为低的)N

(ps： 在算法分析中表示是底数 为2，对数为N，有些地方会写成lgN。)

所以, 通过推导大O阶方法, 时间复杂度为 O(lgN).

【实例 6 】

// 计算阶乘递归 factorial 的时间复杂度？

long factorial ( int N ) {

return N < 2 ? N : factorial ( N - 1 ) * N ;

}

一个一般的递归的时间复杂度计算公式(不是所有递归都适用):

递归的时间复杂度 = 递归的次数 * 每次递归后执行的次数

上述递归:

递归的次数: 当N<2即N=1时, 结束递归, 每次递归-1, 所以congN开始, 共递归了N次

每次递归后执行的次数:每次递归, 只进行了一次三目运算符的判断, 所以执行的次数=1

所以, N*1=N, 通过推导大O阶方法, 时间复杂度为 O(N).

【实例 7 】

// 计算斐波那契递归 fibonacci 的时间复杂度？

int fibonacci ( int N ) {

return N < 2 ? N : fibonacci ( N - 1 ) + fibonacci ( N - 2 );

}

还是用上述公式:

递归的时间复杂度 = 递归的次数 * 每次递归后执行的次数

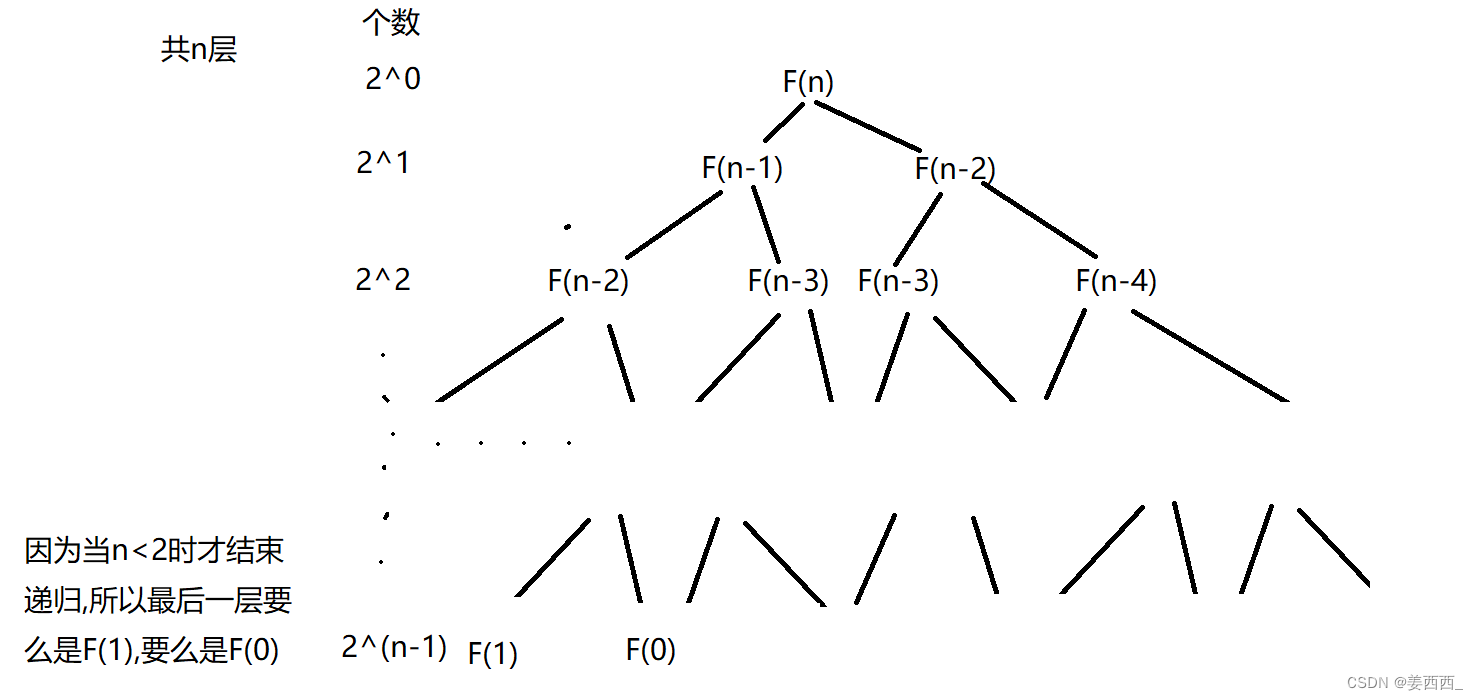
递归的次数:我们画图理解一下

先以F(5)为例:每个F(x)代表一次递归

我们可以看到, 从最上面到最下面, n从5变成了1,也就是一共有五层

第一层有1个数, 第二层有2个数, 第三层有4个数, 我可以得到规律:

第n层有2^(n-1)个数

所以递归的次数为:1+2+4+...+2^(n-1)=2^n +1

每次递归后执行的次数:每次递归, 只进行了一次三目运算符的判断, 所以执行的次数=1

所以, (2^n +1)*1 = 2^n +1, 通过推导大O 阶方法, 时间复杂度为 O(2^N ).

三. 空间复杂度

空间复杂度是对一个算法在运行过程中 临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes 的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大 O 渐进表示法 。

【实例 1 】

// 计算 bubbleSort 的空间复杂度？

void bubbleSort ( int [] array ) {

        for ( int end = array . length ; end > 0 ; end -- ) {

                boolean sorted = true ;

                for ( int i = 1 ; i < end ; i ++ ) {

                        if ( array [ i - 1 ] > array [ i ]) {

                                Swap ( array , i - 1 , i );

                                sorted = false ;

                        }

                }

                if ( sorted == true ) {

                        break ;

                }

        }

}

使用了常数个额外空间，所以空间复杂度为 O(1)

【实例 2 】

// 计算 fibonacci 的空间复杂度？

int [] fibonacci ( int n ) {

        long [] fibArray = new long [ n + 1 ];

        fibArray [ 0 ] = 0 ;

        fibArray [ 1 ] = 1 ;

        for ( int i = 2 ; i <= n ; i ++ ) {

                fibArray [ i ] = fibArray [ i - 1 ] + fibArray [ i - 2 ];

        }

        return fibArray ;

}