《算法通关村——原来这就是堆》

news2024/10/6 1:42:45

《算法通关村——原来这就是堆》

理解最大堆：最大堆就是父节点一定比子节点都要大所以就形成了，自然而然根节点就是最大的值了。

如果在最大堆中要插入值得话，那么就需要把值插入到最后，然后一步一步得走上去，也就是和父节点对比，如果大了，就交换，不大就直接停止了。
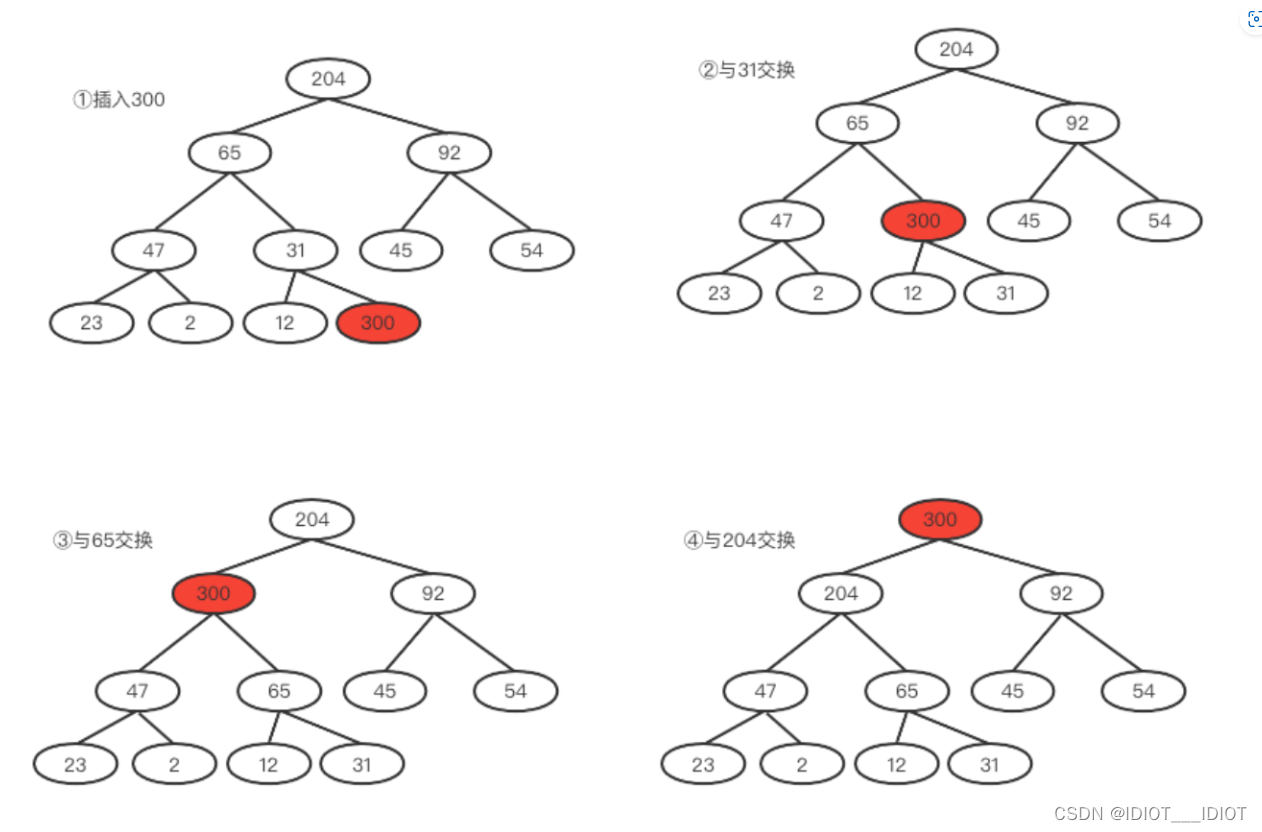
在这里插入图片描述

如果要删除值的话，都是删除最顶端的值，然后把最低端的值拿上来，然后再把这个顶端的值往下面走，如果有比这个值大的就交换（要和子结点中最大的交换），这样就能保证堆的结构不变。
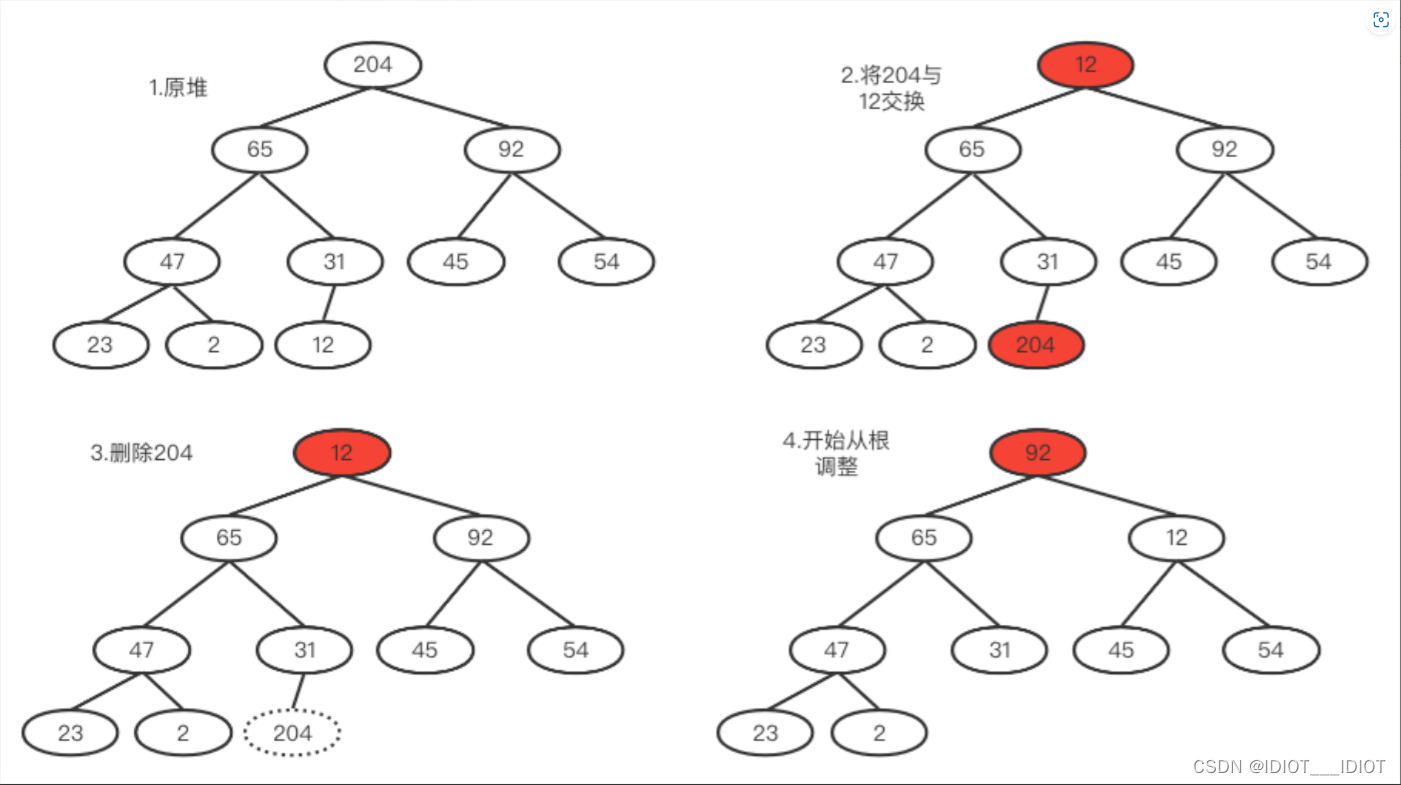
在这里插入图片描述

最大堆的实现（这样子实现只能是值一个一个的插入，才能保证是最大堆，没有办法直接多个插入，如果想多个插入，再建一个构造函数，然后用insert插入就好了。）：

package Algorithm14;

public class MaxHeap {
    private int[] heap;
    private int size;

    public MaxHeap(int capacity) {
        heap = new int[capacity];
        size = 0;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public boolean isFull() {
        return size == heap.length;
    }

    public void insert(int value) throws IllegalStateException {
        if (isFull()) {
            throw new IllegalStateException("Heap is full");
        }

        heap[size] = value;
        bubbleUp(size);
        size++;
    }

    private void bubbleUp(int index) {
        while (index > 0) {
            int parent = (index - 1) / 2;
            if (heap[parent] < heap[index]) {
                swap(parent, index);
                index = parent;
            } else {
                break;
            }
        }
    }

    public int removeMax() throws IllegalStateException {
        if (isEmpty()) {
            throw new IllegalStateException("Heap is empty");
        }

        int max = heap[0];
        heap[0] = heap[size - 1];
        size--;
        bubbleDown(0);
        return max;
    }

    private void bubbleDown(int index) {
        while (true) {
            int child1 = 2 * index + 1;
            if (child1 >= size) {
                break;
            }
            int child2 = child1 + 1;
            int largest = child1;
            if (child2 < size && heap[child2] > heap[largest]) {
                largest = child2;
            }
            if (heap[index] >= heap[largest]) {
                break;
            } else {
                swap(index, largest);
                index = largest;
            }
        }
    }

    private void swap(int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }
}