第九章 动态规划part17
647. 回文子串
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
暴力法:
class Solution {
public:
bool isPalindrome(string s){
int length=s.size();
int start=0;
int end=length-1;
while(s[start]==s[end]&&start<end){
start++;
end--;
}
if(start>=end) return true;
else return false;
}
int countSubstrings(string s) {
int count=0;
for(int i=0;i<s.size();i++){
for(int j=0;j<=i;j++){
string subs=s.substr(j,i-j+1);
if(isPalindrome(subs)) count++;
}
}
return count;
}
};动态规划(看了题解):
状态转移思路跟之前的动态规划不太一样,主要方法是:如果字符串首尾相同,中间是回文串,则该字符串是回文串(特殊情况只有一个元素,两个相同元素),从而可以实现动态规划。
dp[i][j]定义:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
递推公式:如果s[i]==s[j]&&(j-i<=1||dp[i+1][j-1]) dp[i][j]=true
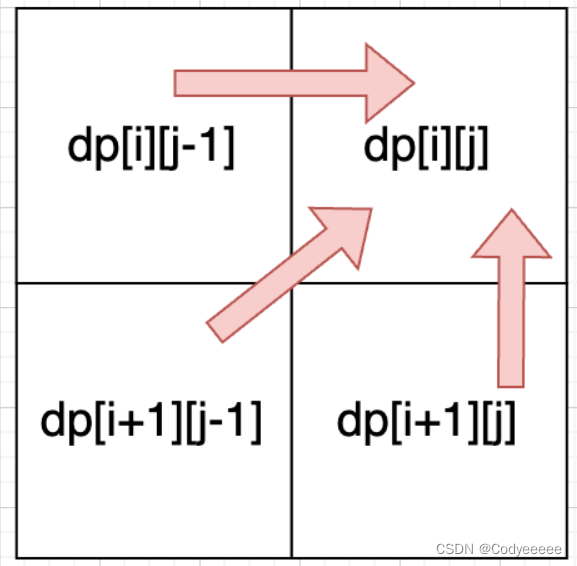
遍历顺序:为确保dp[i+1][j-1]在dp[i][j]之前获得,故遍历顺序为从下到上,从左到右。

class Solution {
public:
int countSubstrings(string s) {
vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
int result=0;
for(int i=s.size()-1;i>=0;i--){
for(int j=i;j<s.size();j++){
if(s[i]==s[j]&&(j-i<=1||dp[i+1][j-1])){
dp[i][j]=true;
result++;
}
}
}
return result;
}
};516. 最长回文子序列
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
跟前面的题思路其实一致,不过还是看了题解。主要不同在于dp的定义。
在本题中dp[i][j]的定义为: 区间范围[i,j] (注意是左闭右闭)的子串的最长回文子序列长度。
递推公式为:
dp[i]==dp[j]时,dp[i][j]=dp[i+1][j-1]+2;
dp[i]!=dp[j]时,dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
初始化,i==j时,即一个字符的最长回文子序列长度为1。
遍历顺序与上一题同。
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
for(int i=0;i<s.size();i++) dp[i][i]=1;
for(int i=s.size()-1;i>=0;i--){
for(int j=i+1;j<s.size();j++){
if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2;
else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][s.size()-1];
}
};