题目
实现一个支持优先级的队列,高优先级先出队列,同优先级时先进先出。
如果两个输入数据和优先级都相同,则后一个数据不入队列被丢弃。
队列存储的数据内容是一个 整数。
输入描述
一组待存入队列的数据(包含内容和优先级)。
输出描述
队列的数据内容(优先级信息输出时不再体现)。
补充说明
不用考虑数据不合法的情况,测试数据不超过100个。
示例1
输入:
(10,1),(20,1).(30,2).(40,3)
输出:
40,30,10,20
说明:
输入样例中,向队列写入了4个数据,每个数据由数据内容和优先级组成。输入和输出内容都不含空格。数据40的优先级最高,所以最先输出,其次是30;10和20优先级相同,所以按输入顺序输出
示例2
输入:
(10,1),(10,1).(30,2).(40,3)
输出:
40,30,10
说明:
输入样例中,向队列写入了4个数据,每个数据由数据内容和优先级组成输入和输出内容都不含空格。
数据40的优先级最高,所以最先输出,其次是30;两个10和10构成重复数据,被丢弃一个。
思路
基础的数据结构题,大概三个思路:
- 直接放入list,转对象排序,可以实现要求
- 使用内置的PriorityQueue对象实现
- 自定义数据结构实现
猜测考察点在第三点,不然前两个虽然能达到目的,但是没有意义
排序实现
分析题目,排序规则为:
- 优先级高的先出,
- 同优先级时位置靠前的先出;
- 数据和优先级均相同的去重
基于以上分析,可以采用以下步骤实现:
- 新建一个data对象,含有priority,val,idx三个属性,idx代表出现位置
- 把输入转为data对象放入list中
- 先去重(利用HashSet),根据priority,val判重,重写equals方法
- 自定义排序规则,priority降序,idx升序排列。Data实现Comparable接口,重写compareTo方法
PriorityQueue实现
还是一样,新建Data对象,重写equals(去重用)和compareTo(排序用)方法
把输入转为Data对象后,直接加入PriorityQueue中
重复对象都加入到了PriorityQueue,在输出时,因为结果已经按照自定义排序规则写好了,所以去重逻辑就是当前项等于上一项时,代表重复,此时不输出对应结果即可
自定义数据结构实现
可以用两个栈实现优先级队列
stackA:优先级高的在栈顶,存放较小优先级
stackB:优先级低的在栈顶,存放较大优先级,也就是说在stackB中的优先级始终比stackA的优先级大,比如某个状态如下:
最后再输出结果时,只需要把stackB依次出栈再入stackA栈,再输出stackA的栈顶元素即可得到:6,5,4,3,2,1。即按优先级降序排列。
具体存放数据逻辑如下,以20 10 30 40 50为例:
存入20,首先判断它是较大优先级还是较小优先级?我们可以和stackB的栈顶元素比较(当然和stackA的栈顶元素比较也可以)。如果cur<stackB.peek()。说明是一个比stackB最低优先级还要小的元素,所以它是一个较小优先级,应该存入stackA中。此处stackB为空,没有栈顶元素,我们也先出入stackA中,由于stackA没有数据,直接存入,如下:
存入10,stackB为空,所以还是存入stackA中,但是此时stackA有数据,由于定义的stackA要将较大优先级放入栈顶,即当前元素如果比stackA的栈顶元素还要小(cur<stackA.peek())时,应该把大于当前优先级的数据转入stackB
存入30,大于stackB的栈顶元素,此时应该存入stackB,同样的逻辑,这里stackB是将优先级小的放入栈顶,所以cur>stackB.peek()时,应该把小于当前优先级的数据转入stackA
存入40,大于stackB栈顶元素,存入stackB,将stackB小于当前优先级的元素放入stackA中
存入50,大于stackB栈顶元素,存入stackB,将stackB小于当前优先级的元素放入stackA中
最后输出结果,需要将stackB中的全部数据转入stackA,再依次从stackA栈顶取数据得到:50 40 30 20 10
上面的过程没有考虑优先级相同和去重时的处理逻辑,现在分析如下:
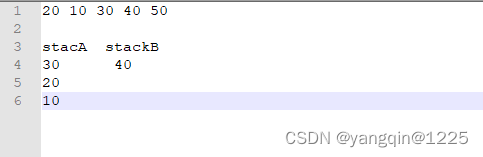
优先级相同,比如在上面的数据中再加入一个30,30小于stackB的栈顶元素,所以应该放入stackA中,将stackA大于30的元素全部弹出来:
关键在于等于30是否弹出?如果弹出,那么我们将第二个30加入到了stackA的栈顶,第一个30弹入了stackB的栈顶,最后输出结果时,一定是先输出的第一个30。符合题意,否则的话,会先输出第二个30。所以在stackA入栈时,判断条件是:cur<=stackA.peek()
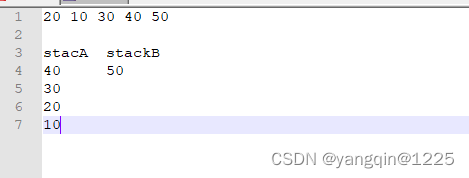
假设最后加入的不是30而是50,此时弹出到stackA时,不应该取等,即cur>stackB.peek(),即只弹出比stackB栈顶元素还大的值
如上,因为栈顶和50相等,不弹出stackA,直接加入,最后的结果一定是第一个50先输出来。去重,根据第一点,优先级相同时的处理逻辑可以发现,当优先级相同时,始终会把之前的数据放入到stackB中去,所以我们再向stackA或者stackB加入数据时,只要判断其不等于stackB的栈顶元素即可(相等判断逻辑为优先级和值同时相同,重写equals方法实现)
题解
三种方法都定义了实体Data:
class Data implements Comparable<Data> {
private int priority;
private int val;
private int idx;
public Data(int priority, int val, int idx) {
this.priority = priority;
this.val = val;
this.idx = idx;
}
public int getIdx() {
return idx;
}
public void setIdx(int idx) {
this.idx = idx;
}
public int getPriority() {
return priority;
}
public void setPriority(int priority) {
this.priority = priority;
}
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public Data(int priority, int val) {
this.priority = priority;
this.val = val;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Data data = (Data) o;
return priority == data.priority &&
val == data.val;
}
@Override
public int hashCode() {
return Objects.hash(priority, val);
}
@Override
public int compareTo(Data o) {
if (this.priority != o.priority) return o.priority - this.priority;
return this.idx - o.idx;
}
}
排序实现
package hwod;
import java.util.*;
import java.util.stream.Collectors;
public class MyPriorityQueue {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String inputs = sc.nextLine();
System.out.println(myPriorityQueue(inputs));
}
/**
* 直接排序输出
*
* @param str
* @return
*/
private static String myPriorityQueue(String str) {
//将输入解析为自定义对象Data
Set<Data> set = new HashSet<>();
String[] arrs = str.substring(1, str.length() - 1).split("\\),\\(");
for (int i = 0; i < arrs.length; i++) {
String[] cur = arrs[i].split(",");
set.add(new Data(Integer.parseInt(cur[1]), Integer.parseInt(cur[0]), i));
}
List<Data> list = set.stream().sorted().collect(Collectors.toList());
StringBuilder sb = new StringBuilder();
for (int i = 0; i < list.size(); i++) {
if (i != 0) sb.append(",");
sb.append(list.get(i).getVal());
}
return sb.toString();
}
}
PriorityQueue实现
package hwod;
import java.util.*;
import java.util.stream.Collectors;
public class MyPriorityQueue {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String inputs = sc.nextLine();
System.out.println(myPriorityQueue(inputs));
}
/**
* 使用java自带的优先级队列
*
* @param str
* @return
*/
private static String myPriorityQueue(String str) {
//将输入解析为自定义对象Data
String[] arrs = str.substring(1, str.length() - 1).split("\\),\\(");
PriorityQueue<Data> queue = new PriorityQueue<>();
for (int i = 0; i < arrs.length; i++) {
String[] cur = arrs[i].split(",");
Data data = new Data(Integer.parseInt(cur[1]), Integer.parseInt(cur[0]),i);
queue.add(data);
}
StringBuilder sb = new StringBuilder();
Data lst = null;
int size = queue.size();
while (!queue.isEmpty()) {
Data data = queue.poll();
if (!data.equals(lst)) {
lst = data;
if (size != queue.size()+1) sb.append(",");
sb.append(data.getVal());
}
}
return sb.toString();
}
}
自定义数据结构实现
package hwod;
import java.util.*;
import java.util.stream.Collectors;
public class MyPriorityQueue {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String inputs = sc.nextLine();
System.out.println(myPriorityQueue(inputs));
}
/**
* 用两个栈实现优先级对列
*
* @param str
* @return
*/
private static String myPriorityQueue2(String str) {
//将输入解析为自定义对象Data
String[] arrs = str.substring(1, str.length() - 1).split("\\),\\(");
Myqueue queue = new Myqueue();
for (int i = 0; i < arrs.length; i++) {
String[] cur = arrs[i].split(",");
Data data = new Data(Integer.parseInt(cur[1]), Integer.parseInt(cur[0]));
queue.add(data);
}
StringBuilder sb = new StringBuilder();
int size = queue.getSize();
while (!queue.isEmpty()) {
if (queue.getSize() != size) sb.append(",");
sb.append(queue.remove().getVal());
}
return sb.toString();
}
}
class Myqueue {
private LinkedList<Data> stackA = new LinkedList<>();//存小数,大堆顶
private LinkedList<Data> stackB = new LinkedList<>(); //存大数,小堆顶
public void add(Data data) {
if (stackB.isEmpty() || data.getPriority() <= stackB.peekLast().getPriority()) {
//比stackB栈顶元素还小,说明是一个较低优先级,应该存在stackA中
//和stackB栈顶元素相等,说明有两个优先级相等的data,比如(30,1),(10,1),题目要求按照输入顺序输出,那么可以等价于后出现的优先级相对更低
// 即此处的优先级等于和小于等价
while (!stackA.isEmpty() && data.getPriority() <= stackA.peekLast().getPriority()) {
stackB.addLast(stackA.removeLast());
}
//优先级相等时,始终会把之前的数据放入stackB中去
if (!stackB.isEmpty() && stackB.peekLast().equals(data)) return;
stackA.addLast(data);
} else {
while (!stackB.isEmpty() && data.getPriority() > stackB.peekLast().getPriority()) {
stackA.addLast(stackB.removeLast());
}
if (!stackB.isEmpty() && stackB.peekLast().equals(data)) return;
stackB.addLast(data);
}
}
public Data remove() {
while (!stackB.isEmpty()) {
stackA.addLast(stackB.removeLast());
}
return stackA.removeLast();
}
public int getSize() {
return stackA.size() + stackB.size();
}
public boolean isEmpty() {
return getSize() == 0;
}
}
推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。