Pix2Pix

• • Pix2Pix 介绍：使用条件 GAN 进行图像到图像的转换
  • Pix2Pix 原理
  • • Pix2Pix 模型结构
    • • 生成器：Unet结构
      • 判别器：PatchGAN
      • 目标函数
  • Pix2Pix 项目使用

 

---

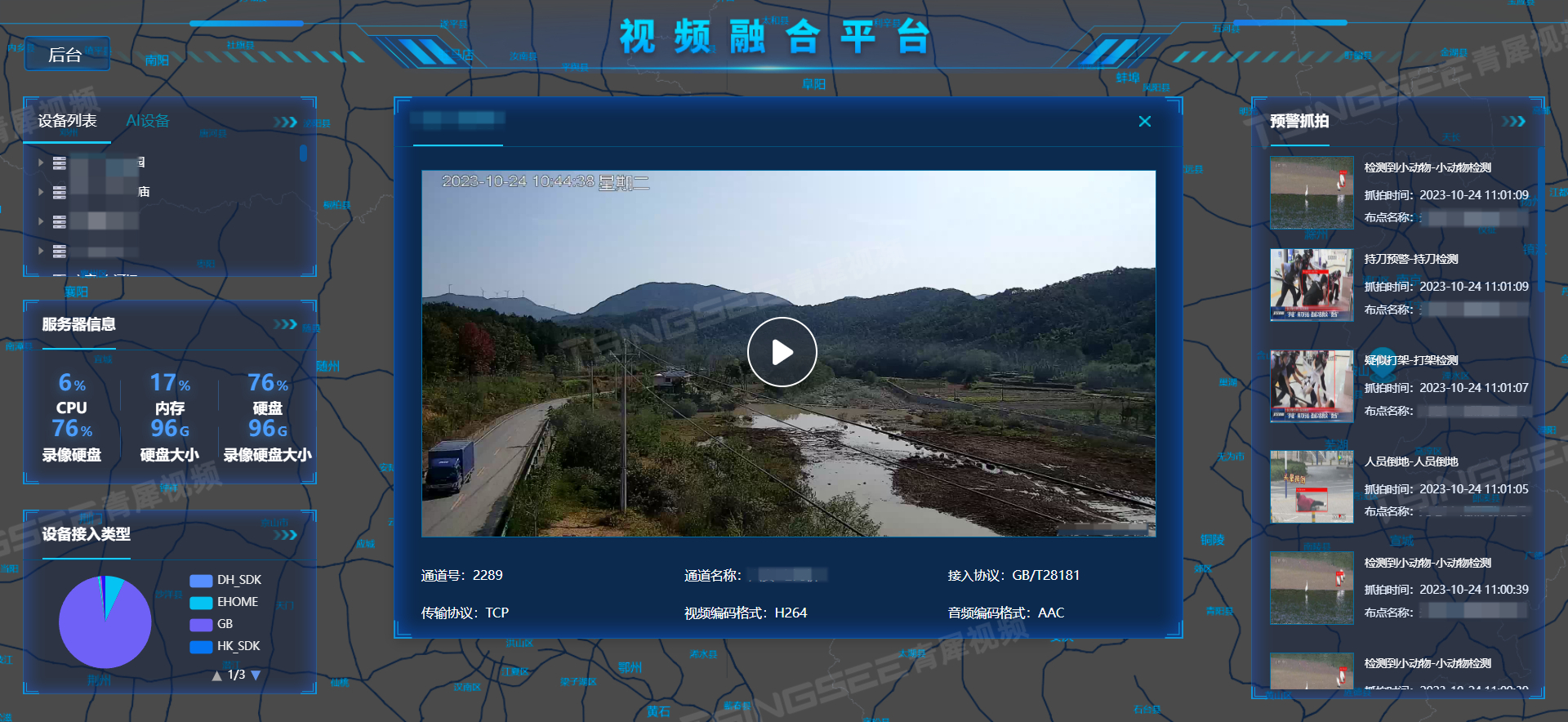
Pix2Pix 介绍：使用条件 GAN 进行图像到图像的转换

Pix2Pix 论文：https://arxiv.org/abs/1611.07004

Pix2Pix 的性质是图像转换。

图像转换，指从一副图像到另一副图像的转换。

可以类比机器翻译，一种语言转换为另一种语言。

这个转换过程是通过建立一个模型，利用生成对抗网络（GANs）的算法，大量的成对图像数据，如简笔画和真实照片，将输入的简笔画转换成逼真的照片。

 

---

Pix2Pix 原理

输入x：简笔画

生成器G：处理简笔画，生成的模拟图

判别器D：

• 输入 {简笔画、生成图}，判断为 fake
• 输入 {简笔画、真实图}，判断为 real

Pix2Pix 模型结构

生成器：Unet结构

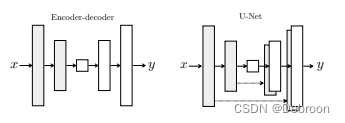
编码器：输入图像，输出特征

解码器：输入特征，输出图像

UNet：对编码-解码器改进的模型，主要是用于医学影像上。

在编码器和解码器之间增加了跳跃连接，使得同一级别的特征图可以在不同阶段进行拼接和融合。

假设我们有一个医学图像分割任务，输入是一张CT扫描图像，输出是图像中病变区域的分割结果。

解码器主要依赖于局部特征，例如像素的颜色、纹理等。

然而，对于复杂的图像分割任务来说，局部特征可能不足以准确地区分不同的区域。

UNet模型引入跳跃连接，关联到上下文信息、全局特征。

而全局特征可能包括图像中病变区域的大小、形状、位置等信息。

通过在解码器中引入跳跃连接，这些全局特征可以指导像素的分类，帮助模型更好地识别病变区域。

判别器：PatchGAN

PatchGAN是为了解决图像处理领域中的一类问题——如何有效地处理模糊和噪声——而提出的。

具体来说，它是为了解决在图像降质过程中产生的模糊和噪声问题，例如在拍照时由于光线不足、镜头移动等因素导致的图像模糊，或者在图像传输过程中引入的噪声等。

通过学习如何处理这些不良因素，PatchGAN能够让模糊的图像变得更加清晰，从而提高图像的质量。

假设你有一张照片，这张照片的某个部分被划出了一个小的正方形区域，而这个区域里面的内容被模糊处理了。

这个模糊处理的部分就叫做"Patch"，而"PatchGAN"就是一种专门用来处理这样模糊图像的算法。

在PatchGAN训练判别器时，不是把整个图片直接放进判别器中进行判别，而是像下面这样，先把一幅图切成 N x N 的小块, 再把每个小块送入判别器中进行判别，最后把整体的结果取平均。

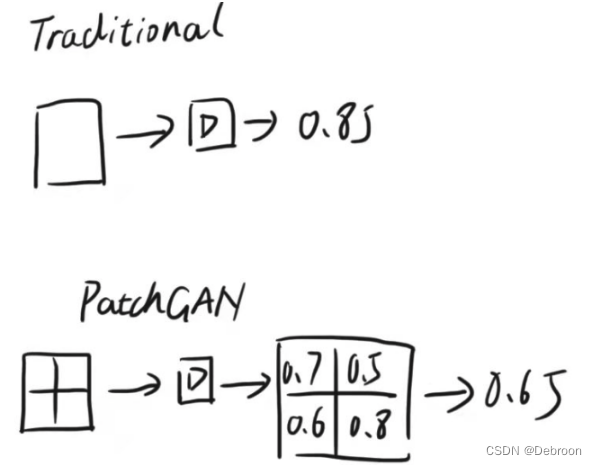
图片来源：CSDN@几维wk

这样划分的好处是，评估高频信息（细节）。

在原始的GAN中，判别器只会输出一个评价值，评价生成器生成的整幅图像。

但是PatchGAN的设计不同，它被设计成全卷积的形式。

这意味着，图像经过各种卷积层后，不会进入全连接层或激活函数，而是使用卷积将输入映射为一个 N*N 的矩阵。

这个矩阵就像原始GAN中的评价值，但它评价的是生成器生成的图像中的每一个小区域。

每个点（true或false）代表原始图像中的一小块区域的评价值，这就是“感受野”的应用。

使用 N*N 的矩阵来评价整幅图像，可以关注更多的区域，这就是PatchGAN的优势。

举例，假设我们有一个 64x64 的图像，我们的 PatchGAN 有 16 个 patch，每个 patch 是 8x8 的。这意味着我们的判别器会输出一个 16x16 的矩阵。每个元素值代表对应 patch 在真实图像中的存在概率。

例如，如果判别器判断第 1 行第 1 列的 patch 是真实的，那么矩阵的第 1 行第 1 列的值就会接近 1，而其他值则会接近 0。如果它判断第 2 行第 3 列的 patch 是生成的，那么矩阵的第 2 行第 3 列的值就会接近 0，而其他值则会接近 1。

通过这种方式，PatchGAN 能够关注到图像中的各个区域，而不仅仅是全局的图像。这对于生成图像的细节部分特别有用，因为往往细节部分更能决定一张图像的真实性。

目标函数

生成器优化目标：$\begin{array}{rl}{\mathcal{L}}_{cGAN}(G,D)=& {\mathbb{E}}_{x,y}[\log D(x,y)]+\\ & {\mathbb{E}}_{x,z}[\log (1-D(x,G(x,z))]\end{array}$

• $LcGAN(G,D)$：这是 cGAN 的损失函数，它关于生成器G和判别器D优化。损失函数的目标是最小化生成器生成的假样本被判别器识别的概率，同时最大化判别器正确识别真实样本的概率。

• $Ex,y[logD(x,y)]$：这部分是期望真实样本被判别器识别的概率。x是真实样本，y是对应的条件标签，D(x,y) 是判别器对于输入 (x,y) 判断为真实样本的概率。

• $Ex,z[log(1-D(x,G(x,z)))]$：这部分是期望生成器生成的假样本被判别器识别的概率。x是真实样本，z是随机噪声，G(x,z)是生成器根据真实样本x和随机噪声z生成的假样本。

  $D(x,G(x,z))$ 是判别器对于输入 $(x,G(x,z))$ 判断为真实样本的概率，因此我们需要最大化它的相反数，即 $(1-D(x,G(x,z)))$。

  通过最小化这个损失函数，cGAN可以训练出能够生成满足给定条件约束的样本的生成器。

举例：

传统的损失函数，如L2或L1损失，旨在最小化生成样本与真实样本之间的差异。这种差异度量方法在生成对抗网络（GAN）中同样重要，因为生成器不仅要能够欺骗判别器，还需要生成与真实数据相似度尽可能高的假样本。

当我们在GAN的目标函数中加入传统的损失时，生成器就需要在满足判别器的条件下，尽可能地接近真实样本。这使得生成器不仅要关注欺骗判别器，还要关注生成样本的质量。因此，这种结合可以产生更清晰、更逼真的假样本。

L2损失会最小化每个特征的平方差，因此生成的假样本可能会更加平滑，而无法捕捉到真实样本中的一些细节和变化。

相反，如果使用L1损失来优化生成器，我们可能会发现生成的假样本更加锐利和清晰。

这是因为L1损失会最小化每个特征的绝对差值，因此生成的假样本可能会更加突出真实样本中的一些边缘和细节。

所以，在GAN的目标函数中混入L1损失相比L2损失能够带来更好的效果。因为L1损失能够更好地捕捉到真实样本中的边缘和细节，从而产生更清晰、更逼真的假样本。

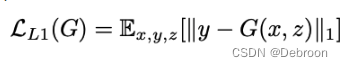
这个公式的目的是最小化生成模型G生成的假样本与真实样本之间的差异。具体来说，它计算了真实样本y与生成模型G生成的假样本G(x, z)之间的L1距离（即绝对值差异的总和）。

最终目标函数：

Pix2Pix 项目使用

Pix2Pix 本地部署：https://www.iotword.com/15549.html

Pix2Pix 项目代码：https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix

Pix2Pix 代码（国内下载链接，很快）：https://gitcode.net/zhenzhidemaoyi/pytorch-CycleGAN-and-pix2pix

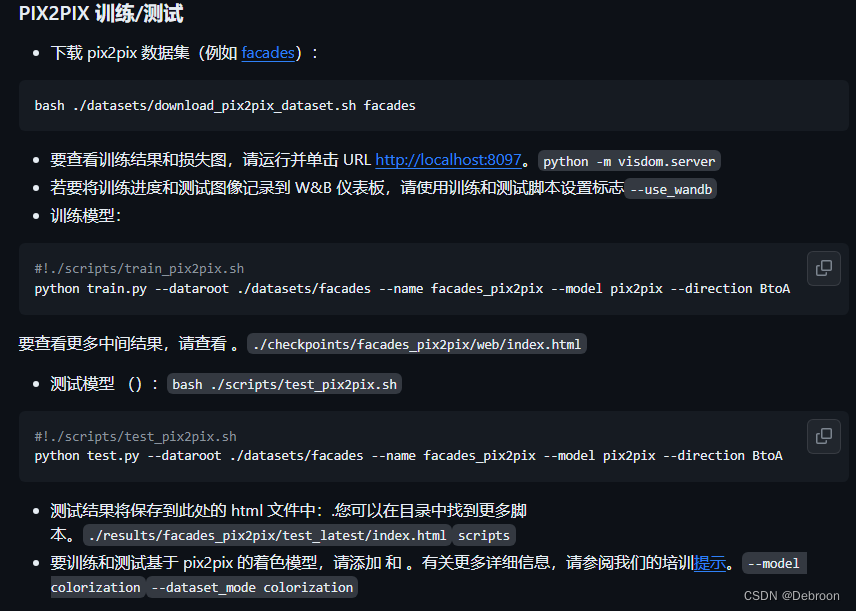
手把手教学使用链接：https://blog.csdn.net/qq_42691298/article/details/127460187

这篇写的太详细，手把手教学，我真没必要再写了。
 

---