Einstein学画画

题目描述

Einstein 学起了画画。

此人比较懒~~，他希望用最少的笔画画出一张画……

给定一个无向图，包含 $n$ 个顶点（编号 $1\sim n$），$m$ 条边，求最少用多少笔可以画出图中所有的边。

输入格式

第一行两个整数 $n,m$。

接下来 $m$ 行，每行两个数 $a,b$（$a\ne b$），表示 $a,b$ 两点之间有一条边相连。

一条边不会被描述多次。

输出格式

一个数，即问题的答案。

样例 #1

样例输入 #1

5 5
2 3
2 4
2 5
3 4
4 5

样例输出 #1

1

提示

对于 $50\%$ 的数据，$n\le 50$，$m\le 100$。

对于 $100\%$ 的数据，$1\le n\le 1000$，$1\le m\le {10}^5$。

---

思路

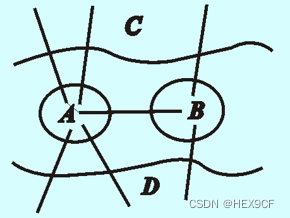
欧拉通路：经过所有顶点且每条边恰好经过一次的通路
欧拉回路：经过所有顶点且每条边恰好经过一次的回路
欧拉图：有欧拉回路的图

根据欧拉图判别定理，无向图G具有欧拉回路当且仅当G是连通的且无奇度顶点。当没有奇度定点时，该图为欧拉图，存在经过所有顶点且每条边恰好经过一次的回路，可以一笔画，直接输出1。

无向图G具有欧拉通路、但没有欧拉回路，当且仅当G是连通的且有2个奇度顶点，其余顶点均为偶度数的，这2个奇度顶点是每条欧拉通路的端点。当奇度定点只有两个时，也可以一笔画。

无向图奇度点的个数一定是偶数个，因为每加一条边，总度数加2。每多两个奇度点，笔画数多1，所以输出 odd / 2。

---

AC代码

#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;

const int N = 1e6 + 7;

int n, m;
int d[N];
int odd;

int main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		int a, b;
		cin >> a >> b;
		d[a]++;
		d[b]++;
	}
	odd = 0;
	for (int i = 1; i <= n; i++) {
		if (d[i] % 2) {
			// 奇度顶点
			odd++;
		}
	}
	if (odd) {
		cout << odd / 2 << endl;
	} else {
		cout << 1 << endl;
	}
	return 0;
}