70. 爬楼梯 （进阶）

题目链接：

题目页面

求解思路：

动规五部曲

1. 确定dp数组及其下标含义：爬到有i阶楼梯的楼顶，有dp[i]种方法
2. 递推公式：dp[i] += dp[i-j];
3. dp数组的初始化：dp[0] = 1;
4. 确定遍历顺序：排列问题，先遍历物品，再遍历背包；完全背包，遍历顺序都为正序
5. 举例推导dp数组：

代码：

#include <iostream>
#include <vector>
using namespace std;

int main(){
    int n, m;
    cin >> n >> m;
    vector<int> dp(n+1, 0);
    dp[0] = 1;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= m; j++){
            if (i >= j) dp[i] += dp[i-j];
        }
    }
    cout << dp[n] << endl;
}

322. 零钱兑换

题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

求解思路：

动规五部曲

1. 确定dp数组及其下标含义：凑足总额为j所需钱币的最少个数为dp[j]
2. 确定递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3. dp数组的初始化：dp[0] = 0，因为凑足0元所需的钱币个数是0；其余下标初始化为int的最大值，为了避免递推公式中初始值覆盖结果值
4. 确定遍历顺序：这里求钱币最小个数，和顺序没有关系，不强调组合或是排列，因此先遍历背包或是物品都可以；因为是完全背包，所以都是正序遍历
5. 举例推导dp数组：coins = [1, 2, 5], amount = 5为例，如图

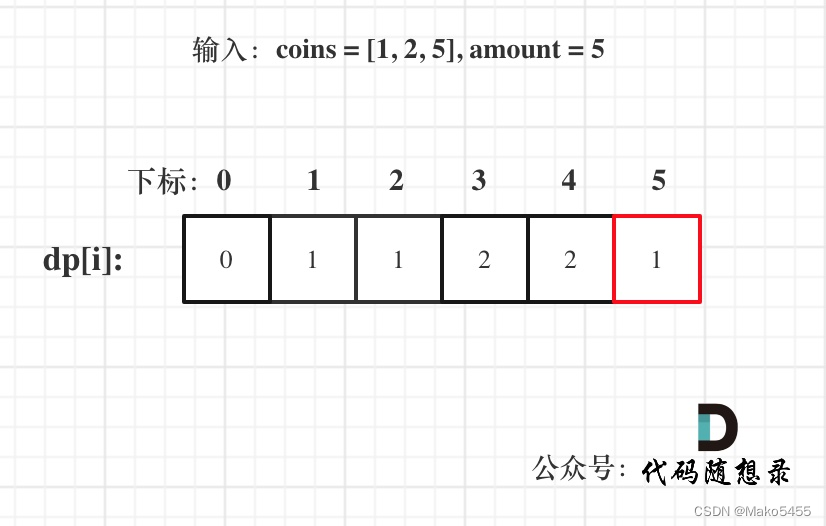
代码：

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1, INT_MAX);
        dp[0] = 0;
        for (int i = 0; i < coins.size(); i++){
            for (int j = coins[i]; j <= amount; j++){
                if (dp[j-coins[i]] != INT_MAX)
                    dp[j] = min(dp[j], dp[j-coins[i]]+1);
            }
        }
        if (dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

279.完全平方数

题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

求解思路：

动规五部曲

1. dp数组及其下标含义：和为j的完全平方数的最少数量为dp[j]
2. 递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);
3. dp数组的初始化：dp[0] = 0；其余下标初始化为int的最大值
4. 确定遍历顺序：先遍历物品或背包都可以；因为是完全背包，所以都是正序遍历
5. 举例推导dp数组：n=5，如图

代码：

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1, INT_MAX);
        dp[0] = 0;
        for (int i = 0; i <= n; i++){
            for (int j = 1; j * j <= i; j++){
                dp[i] = min(dp[i], dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};