1. 概述

聚类算法是一种无监督学习方法，用于将数据集中的对象分组或聚集成具有相似特征的集合，该集合被称为簇(cluster)。聚类算法通过计算数据点之间的相似性或距离，将相似的数据点归为同一簇，使簇内差距最小化，簇间差距最大化，从而将数据集划分为多个互相区分的组。聚类算法的目标是在无标签的情况下，发现数据中的内在结构和模式。聚类算法可以发现数据中的隐藏模式、异常值或离群点，以及进行数据预处理和可视化。

---

监督学习：通过训练集中的已知输入和对应的标签来构建一个模型，然后使用该模型对未知的输入数据进行预测或分类。
无监督学习：训练集中的数据没有对应的标签，通过分析输入数据的内在结构和关联，对数据进行聚类、降维、异常检测等操作。
半监督学习：介于监督学习与无监督学习之间，它要求对小部分的样本提供预测量的真实值。这种方法通过有效利用所提供的小部分监督信息，通常可以获得比无监督学习更好的效果，同时也把获取监督信息的成本控制在可以接受的范围。

相关分类：

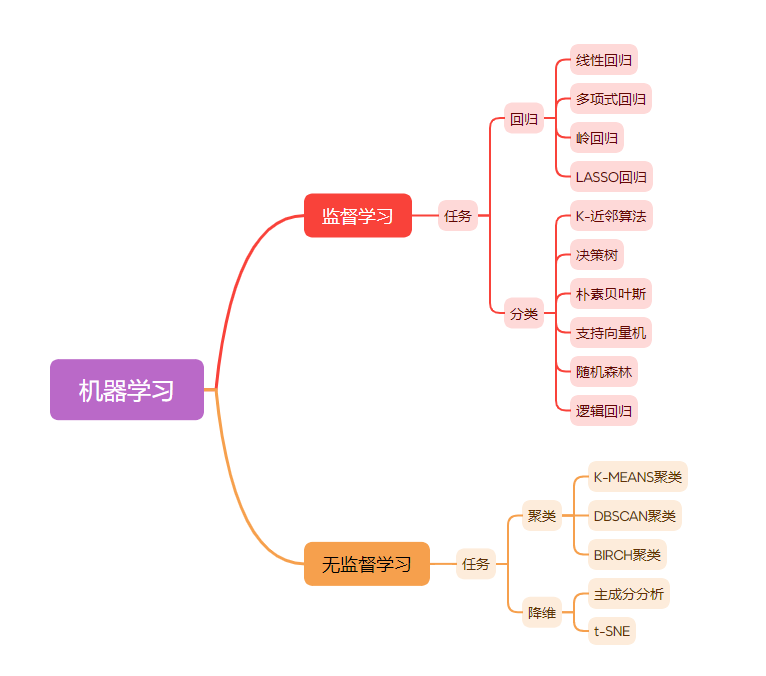
2. K-MEANS算法

算法思想：以空间中的 K 个点为中心进行聚类，对最靠近他们的对象进行归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。

2.1 工作流程

1. 先从没有标签的元素集合 A 中随机取 K 个元素，作为 K 个簇各自的质心。
2. 分别计算剩下的元素到 K 个簇的质心的距离（可以使用欧氏距离），根据距离将这些元素划归到最近的簇。
3. 根据聚类结果，重新计算质心（计算子集中所有元素各个维度的算数平均数）。
4. 将集合 A 中所有元素按照新计算的质心重新进行聚类。
5. 重复第3-4步，直到所有质心不再发生变化。

2.2 代码实践

from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

# 载入数据，以空格分隔数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")
# 训练模型，设置4个聚类中心
model = KMeans(n_clusters=4)
model.fit(data)
# 聚类中心点坐标
centers = model.cluster_centers_
# 预测结果，也可以通过model.labels_查看模型中各样本点的类别
result = model.predict(data)

# 用不同颜色表示类别
mark = ['or', 'ob', 'og', 'oy']

# enumerate用于在迭代过程中同时获取元素的索引和值
for i,d in enumerate(data):
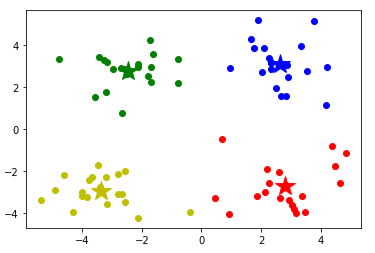
    plt.plot(d[0], d[1], mark[result[i]])

# 画出各个聚类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):
    plt.plot(center[0], center[1], mark[i], markersize=20)

# 获取数据值所在的范围，这里的+1、-1是为了不让样本点出现在边框上
# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1

# 生成网格矩阵元素
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

#--------------------------------------------------------#
# 预测分类结果
# ravel()：将多为数据展平为一维数据
# np.c_：按列连接两个数组，即拼接成点的坐标的形式
# contourf(xx, yy, z)：创建填充等高线图，参数需为二维数组
#--------------------------------------------------------#
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
cs = plt.contourf(xx, yy, z)

# 绘制样本点
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):
    plt.plot(d[0], d[1], mark[result[i]])

# 绘制各个聚类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):
    plt.plot(center[0],center[1], mark[i], markersize=20)

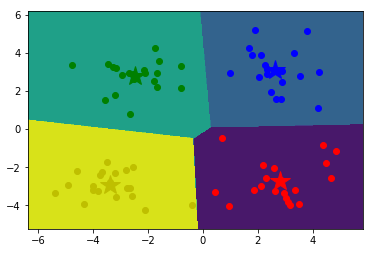
2.3 Mini Batch K-Means

Mini Batch K-Means 算法是 K-Means 算法的变种，采用小批量的数据子集减小训练时间。这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，使用这些数据子集训练算法可以减小训练时间，且结果一般只略差于标准算法。

迭代步骤：

1. 从数据集中随机抽取小批量数据，把他们分配给最近的质心
2. 更新质心

代码中Mini Batch K-Means算法的导入

from sklearn.cluster import MiniBatchKMeans

其余代码部分与K-MEANS算法一致。

2.4 存在问题

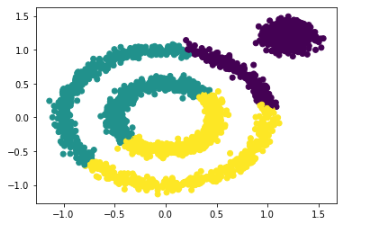
K-MEANS算法在处理非球状的数据时存在局限性，如下图圈状数据的聚类。

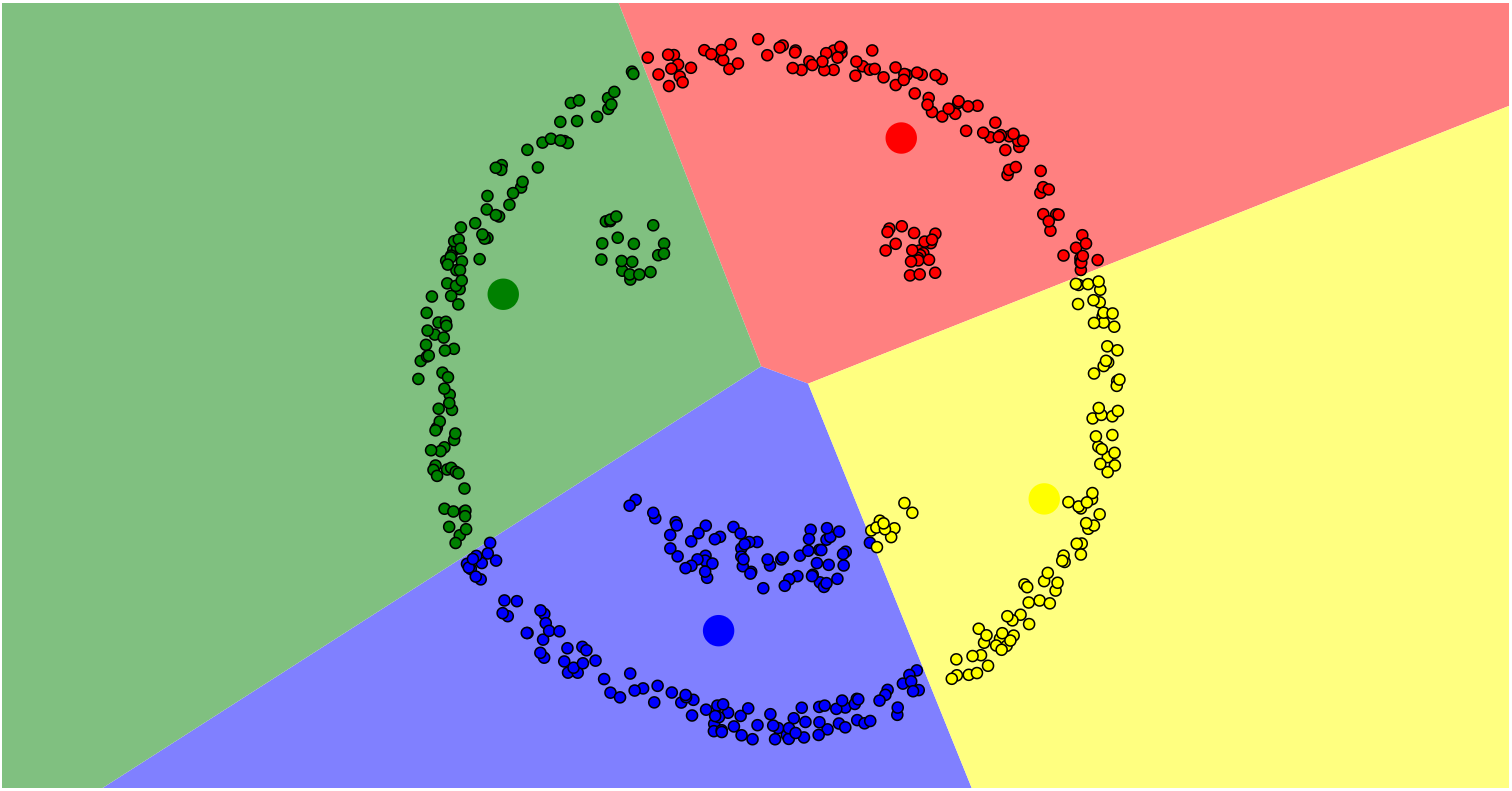
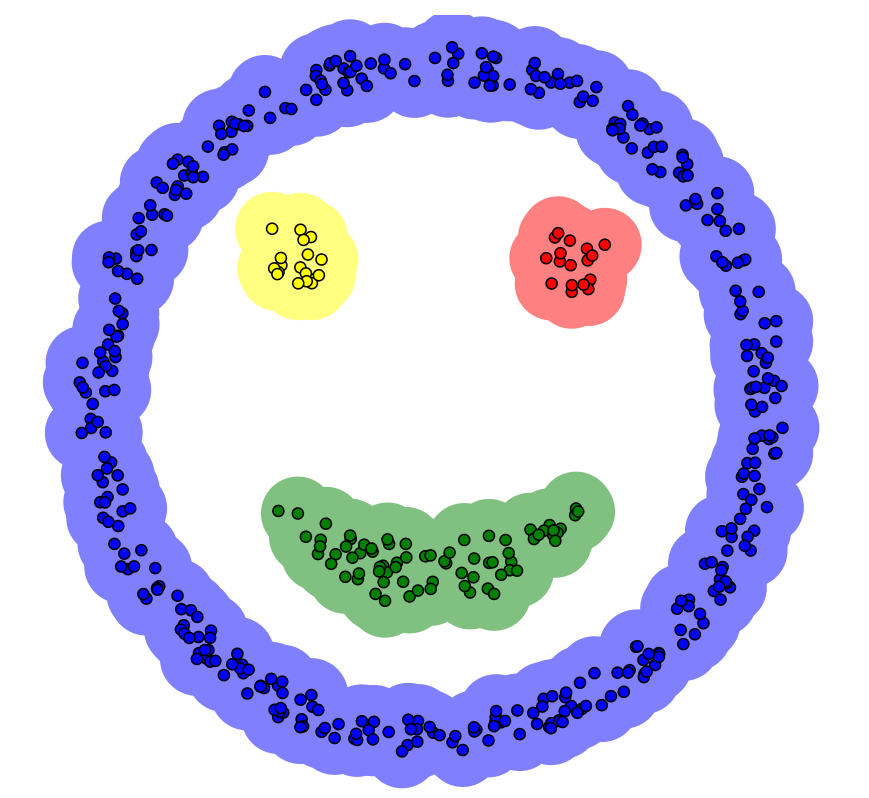
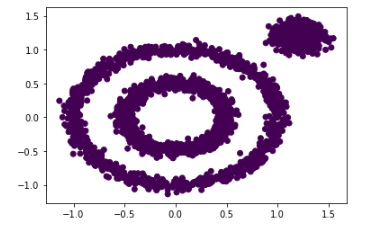
聚类结果显然不理想（外层圈状数据应归为一类），而使用DBSCAN算法后的聚类结果如下，效果明显优于K-MEANS算法，下面将介绍DBSCAN算法。

2.5 K-MEANS可视化

可视化网站
效果图：

3. DBSCAN算法

DBSCAN（Density-Based Spatial Clustering of Applications with Noise：基于密度的带噪声空间聚类算法）算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，算法将“簇”定义为密度相连的点的最大集合。基于密度的聚类是寻找被低密度区域分隔的高密度区域。

3.1 基本概念

𝛆-邻域：给定对象（数据点）半径 𝜀 内的区域称为该对象的 𝜀 邻域。
核心对象：如果给定 𝜀 邻域内的样本点数大于等于 Minpoints（自定义的阈值），则该对象为核心对象。
密度直达：给定一个对象集合$D$，如果$p$在$q$的 𝜀 邻域内，且$q$是一个核心对象，则称 $p$ 由 $q$ 密度直达，如图 $x_1$ 和 $x_2$。
密度可达：如果存在样本序列$p_1,p_2,\dots ,p_n$，其中$p_1=q$，$p_n=p$，且$p_{i+1}$由$pi$密度直达，则称点 $p$ 由 $q$ 密度可达，如图 $x_1$ 和 $x_3$。
密度相连：若存在点 $k$，使得点 $p$ 和 $q$ 均由 $k$ 密度可达，则称 $p$ 和 $q$ 密度相连，如图 $x_3$ 和 $x_4$。

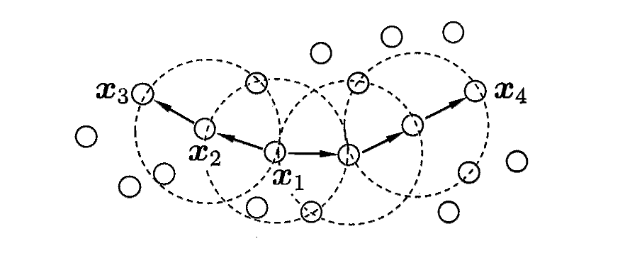
DBSCAN算法中点的分类：

1. 核心点：在半径 𝜀 内含有至少 Minpoints 个数据点，则该点为核心点。
2. 边界点：在半径 𝜀 内，含有点的数量小于 Minpoints，但是属于核心点的邻居。
3. 噪声点：既不是核心点也不是边界点的点。

3.2 工作流程

1. 指定合适的 𝜀 和 Minpoints。
2. 随机选择一个未被访问的数据点 $p$。
3. 如果 $p$ 的ε-邻域中包含至少 Minpoints 个数据点，则将 $p$ 标记为核心点，并创建一个新的簇。
4. 从 $p$ 的ε-邻域中选择一个未被访问的数据点 $q$，并将其加入到当前簇中。如果 $q$ 也是一个核心点，则将 $q$ 的ε-邻域中的未被访问的数据点也加入到当前簇中。
5. 重复步骤4，直到当前簇中的所有核心点的ε-邻域都被访问过。
6. 重复步骤2-5，直到所有的数据点都被访问过。

3.3 代码实践

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#-------------------------------------------------------------------------------------#
# make_circles：生成二维环状数据集
# factor：表示内圈和外圈之间的比例因子，默认为0.8
# make_blobs：生成服从高斯分布的数据集
# cluster_std：数据集标准差
#-------------------------------------------------------------------------------------#
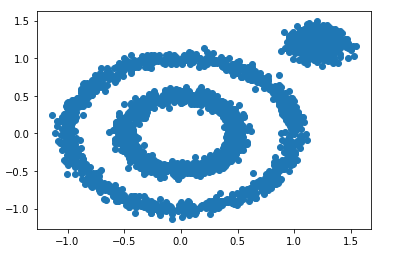
x1, y1 = datasets.make_circles(n_samples=2000, factor=0.5, noise=0.05)
x2, y2 = datasets.make_blobs(n_samples=1000, centers=[[1.2,1.2]], cluster_std=[[.1]])

x = np.concatenate((x1, x2))
plt.scatter(x[:, 0], x[:, 1], marker='o')

from sklearn.cluster import KMeans
# 拟合KMeans算法模型并返回所有样本聚类后的类别
y_pred = KMeans(n_clusters=3).fit_predict(x)
# 绘制聚类结果
plt.scatter(x[:, 0], x[:, 1], c=y_pred)

from sklearn.cluster import DBSCAN
#----------------------------------------------------#
# 拟合DBSCAN算法模型并返回所有样本聚类后的类别
# DBSCAN()中参数eps默认为0.5，min_samples默认为5
#----------------------------------------------------#
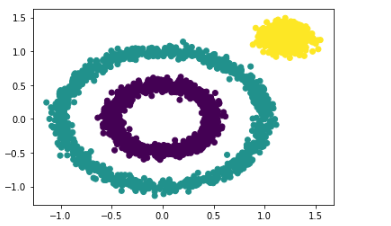
y_pred = DBSCAN().fit_predict(x)
# 绘制聚类结果
plt.scatter(x[:, 0], x[:, 1], c=y_pred)

#----------------------------------------------------#
# 拟合DBSCAN算法模型并返回所有样本聚类后的类别
# DBSCAN()中参数eps默认为0.5，min_samples默认为5
#----------------------------------------------------#
y_pred = DBSCAN(eps = 0.2).fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)

3.4 DBSCAN算法可视化

可视化网站