前言:
在链式二叉树中,我们一般都是通过一个建立好的二叉树从而算出他的前序遍历,那么如何通过一个前序遍历来创建一个二叉树呢,本文将详细解读前序遍历每一个步骤是如何创建二叉树的。
1、分析前序遍历,构建出二叉树
现有前序遍历:abc##de#g##f###,其中‘#’号表示NULL。由于前序遍历的顺序为:根结点-左子树-右子树,因此该前序遍历的第一个字符表示的是整个树的根结点,既字符a是根结点。下一个字符按照前序遍历的顺序应该是根结点a的左子树也就是b为a的左子树:

这时候根(a)-左子树(b)的顺序已经走完,下一个理应是右子树,但是这时候b被看成了一个根结点,因此顺序又回到了根结点(b)-左子树-右子树,该前序遍历的下一个字符c被当成b的左子树:

此时根(b)-左子树(c)顺序已经走完,按理来说应该到根(b)-左子树(c)-右子树(#),但是情况和上面一样,把c看成了根结点,则该前序序列的下一个字符‘#’号是c的左子树。但是‘#’号表示的是NULL,因此走到‘#'号时不会把’#‘当成一个根结点来看待了,所以会走完根结点c的顺序,既:根(c)-左子树(#)-右子树(#),如下图:

现在终于完整的走完了一次前序遍历的顺序,接着就是往上”收回“,因为结点c下面两个孩子结点都为NULL,因此不会再往下走。结点c遍历结束后,表示的是b的左子树完成, 那么接着刚刚结点b的前序遍历:此时根(b)-左子树(c),接下来应该是根结点b的右子树,因此把该序列的下一个字符d看成是b的右子树:

现在虽然根结点b完成了他的树,但是结点d的两个孩子结点也是需要填写的,逻辑也是前序遍历的逻辑:根结点(d)-左子树-右子树,该序列的下一个字符看成d的左子树:
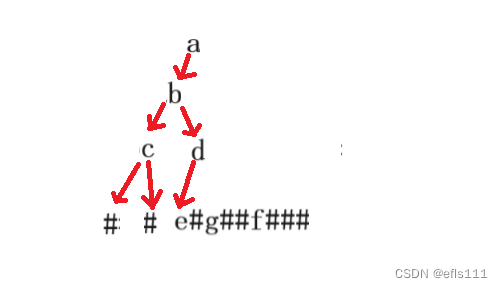
此时,结点e不是NULL,他还是一个结点,因此他也会被当成根结点,继续属于他的顺序,则下一个字符’#‘号是e的左子树,’#‘号不会被当成根结点,因此g被看成是e的右子树:
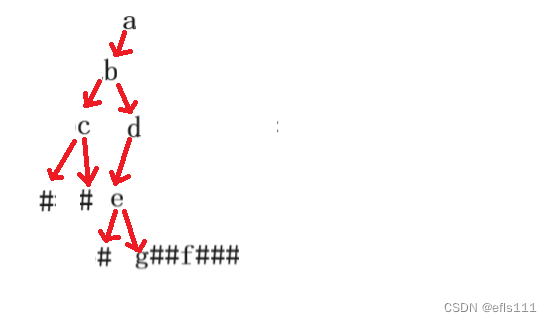
结点g的逻辑同结点e一样,他也被看成一个结点,因此也有属于g的孩子结点,则该序列的后两个’#‘号是g的左右孩子:
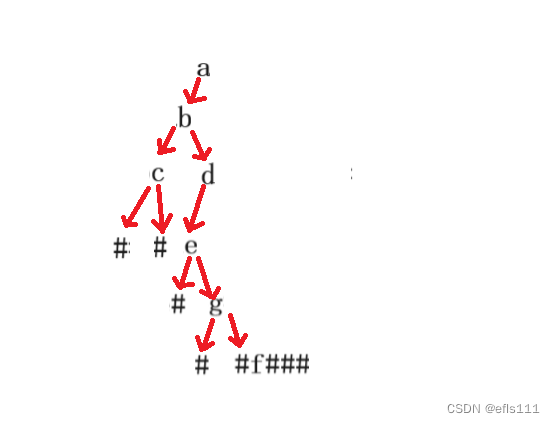
此时g结点的孩子结点都是NULL,代码g作为根结点的前序顺序结束,这时候要进行”收回“,通过上图可以看到,d的右子树还没有进行遍历,因此”收回“至d的左子树处,遍历d的右子树:

可以看到,d的右子树并不是NULL,是一个结点f,因此逻辑相同:
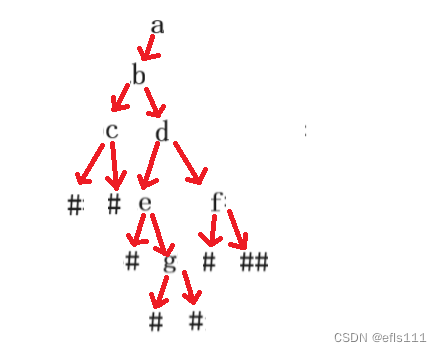
f的两个孩子结点都是NULL,表示f作为根结点的前序顺序完成,又表示根结点a的左子树全部完成,因此“收回”至根结点a的左子树处,接下来就是遍历根节点a的右子树,可以看到序列中只剩下一个’#‘号了,所以根结点a的右子树其实就是一个NULL:

2、代码实现及验证
将以上思想转换成代码形式,并且用中序遍历打印该树,观察结果的正确性,前序遍历:abc##de#g##f###可以看成是字符串,因此用数组的形式将其存储。构建二叉树代码如下:
#include <stdio.h>
#include <stdlib.h>
//创建树节点结构体
typedef int TreeDataType;//int类型重定义
typedef struct TreeNode
{
TreeDataType data;
struct TreeNode* left;
struct TreeNode* right;
}TNode;
//创建树节点
TNode* CreatTreeNode(int x)
{
TNode* treenode = (TNode*)malloc(sizeof(TNode));
if (treenode == NULL)
{
perror("malloc");
return NULL;
}
treenode->data = x;
treenode->left = NULL;
treenode->right = NULL;
return treenode;//返回创建号的树节点地址
}
//利用前序遍历构建树
TNode* CreatTree(char* arr, int* pi)
{
if (arr[(*pi)] == '#')//当数组内遍历到#号,表示空,直接返回即可
{
(*pi)++;//遍历数组
return NULL;
}
TNode* poi = CreatTreeNode(arr[(*pi)]);//走到此处表示遍历数组遇到的不是#,则创建结点
(*pi)++;//遍历数组
//递归思想
poi->left = CreatTree(arr, pi);//将该结点看成根结点,去创建他的左子树
poi->right = CreatTree(arr, pi);//将该结点看成根结点,去创建他的右子树
return poi;//返回该结点的地址给到上一层结点,将他们相连(递归思想)
}
//中序遍历
void InOrder(TNode* boot)
{
if (boot == NULL)
{
return;
}
InOrder(boot->left);//遍历左子树
printf("%c ", boot->data);//打印该结点的值,既打印根节点的值
InOrder(boot->right);//遍历右子树
}
//主函数
int main() {
char arr[100];//创建一个数组用于保存前序遍历,因此可以把前序遍历看成一个字符串
scanf("%s", arr);
int i = 0;//i为数组的下标,用于遍历数组
TNode* root = CreatTree(arr, &i);//用前序遍历构建树
InOrder(root);//中序遍历检查结果
return 0;
}运行结果:
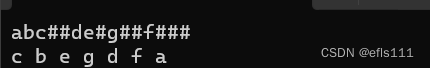
从运行结果来看,中序遍历为:c b e g d f a,中序遍历的顺序为:左子树-根-右子树,根据上文构建出来的二叉树来进行验证该树的中序遍历是否为c b e g d f a:
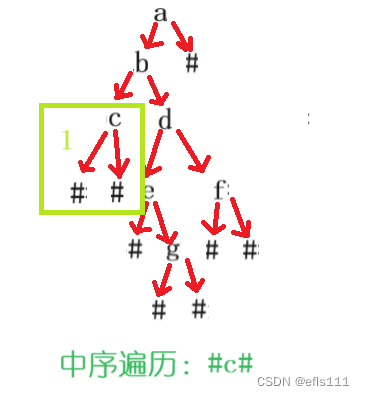
待到方框1中遍历结束后,表示b的左子树遍历完成,根据中序遍历的顺序,下一步就是遍历根结点也就是结点b,然后是结点b的右子树d:

当遍历结点d时,会把结点d当作根结点,因此顺序重新由左子树-根-右子树开始,会先遍历e结点,当遍历到e的右子树g时,逻辑也一样会把g当作根结点从而重新开始遍历g结点:
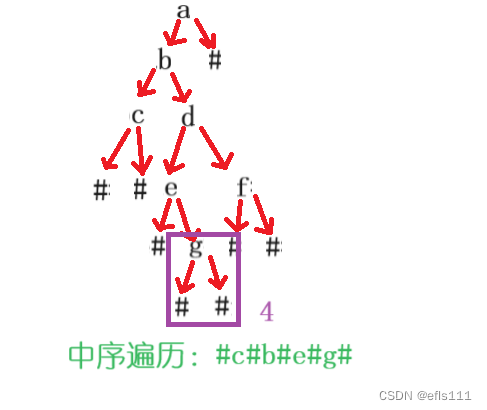
方框4中结束后,表示d的左子树遍历完成,根据中序遍历顺序,下一个是遍历根也就是根结点d,然后是遍历d的右子树f,遍历结点f道理也一样,把f当成根结点并从f的左子树开始遍历:
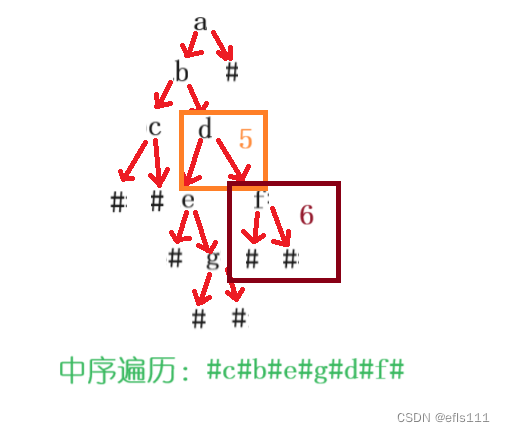
方框6中结束后,表示根结点a的左子树全部遍历完毕,按照中序遍历顺序,左子树完成后下一个是根结点,因此遍历根结点a,最后是遍历a的右子树,a的右子树为空因此最终的顺序如下:
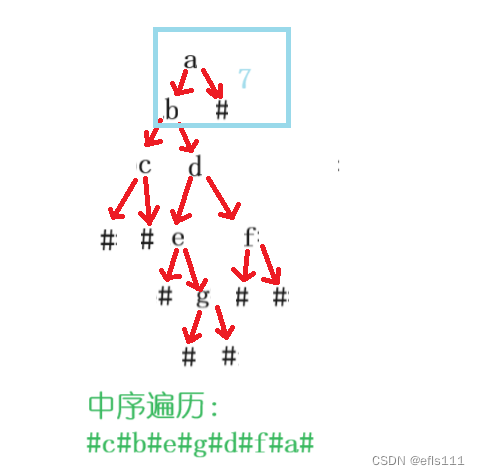
从上图可以看到最后的顺序和代码执行后的中序遍历顺序是一样的,因此说明该代码确实可以通过前序遍历创建出二叉树。
结语:
以上就是关于如何通过前序遍历创建出一个二叉树,尽管这个二叉树很复杂,但是最终还是能够实现出来的,并且其中的每一步遍历都蕴含了递归的思想,细品则会发现更深层次的递归二叉树实现。希望通过以上步骤能够加深你对二叉树的理解(●'◡'●)。