OSG编程指南＜九＞：坐标系统及坐标系变换

1、坐标系统

坐标系是一个精确定位对象位置的框架，所有的图形变换都是基于一定的坐标系进行的。对于从事计算机图形学的研究者，掌握图形变换是不可或缺的，因此，理解坐标系非常重要。一个三维图形工作者可以认为自己站在一定的坐标系中，通过自己的想法来操控模拟的虚拟环境。无论何时何地，只要确定原点和坐标轴的方向，都可以非常方便地建立坐标系。通常来说，任何一个三维坐标系都能表示空间中的所有点，因为坐标轴可以无限延伸。但为了方便处理各种问题，习惯上常定义多种坐标系。这些坐标系在本质上没有好坏之分，只是在不同的情况下处理问题的简化程度不同。
三维坐标系总体上可以分为两大类，即左手坐标系和右手坐标系，相信读者对这两种坐标系都有所了解，这里就不再介绍。常用的坐标系有世界坐标系、物体坐标系和摄像机坐标系，下面分别进行介绍。

1.1 世界坐标系

世界坐标系是一个特殊的坐标系，它建立了描述其他坐标系所需要的参考框架。从另一方面说，能够用世界坐标系来描述其他坐标系的位置，而不能用更大的、外部的坐标系来描述世界坐标系。世界坐标系也被广泛地称为全局坐标系或宇宙坐标系。世界坐标系描述的是整个场景中的所有对象，可以理解为绝对坐标系，所有对象的位置都是绝对坐标。
从整体上考虑，它为所有对象的位置提供一个绝对的参考标准，从而避免了物体之间由于各自独立的物体坐标系而导致的坐标系混乱。世界坐标系通常描述的问题是一些对象的初始位置及场景中对象的变换过程，对象主要包括摄像机和绘制的物体。

1.2 物体坐标系

物体坐标系是针对某一特定的物体而建立的独立坐标系。每一个物体都有自己的坐标系，当物体发生变换时，实际上是它本身的坐标系相对于世界坐标系发生变换的过程。物体坐标系对于描述特定的物体非常方便，假设所有的物体都用一个世界坐标系来描述，则一个物体进行任何变换的计算量都非常大，包括顶点坐标变换等。定义物体坐标系之后，非常容易即可实现物体的变换，只需要对物体坐标系相对世界坐标系发生变换即可。
如果用世界坐标系来描述一个人，很难确定人的各个器官的精确坐标，从而人体模型的建立就非常困难，这时可以充分体现物体坐标系描述特定物体的优势。物体坐标系通常描述的问题是特定物体的内部对象，主要包括物体的顶点、物体的法向量和物体的方向。

1.3 摄像机坐标系

摄像机坐标系是和观察者密切相关的坐标系。摄像机坐标系和屏幕坐标系相似，差别在于摄像机坐标系处于 3D 空间中，而屏幕坐标系在 2D 平面里。摄像机坐标系可以被看作是一种特殊的物体坐标系，该物体坐标系就定义在摄像机的屏幕可视区域。
摄像机坐标系描述的是物体是否绘制渲染，并且在屏幕上显示出来。可以这样认为，即使视野再宽广，也无法一眼看到整个世界，这样读者就会发现摄像机坐标系的意义所在。
摄像机坐标系描述的问题是哪些物体应该绘制渲染并且显示在屏幕上，主要包括物体是否在摄像机坐标系区域内、物体的渲染顺序和物体的遮挡绘制。因此，摄像机坐标系描述的问题是非常复杂的，一个好的虚拟引擎在这方面的表现肯定会非常突出，如区域裁剪、物体的遮挡渲染等。
对于坐标系基本了解以后，读者可能会发现其中并没有涉及 OSG，这是因为前面讲解的都是一些基本的概念，只有了解了这些基础知识后才能够轻松理解后面的内容。OSG 对于上面所描述的 3 种坐标系都有比较好的应用，具体实现可参见源代码。OSG 采用的世界坐标系是左手坐标系，这点与 OpenGL 是保持一致的。值得注意的是它们之间的坐标轴方向不一样。

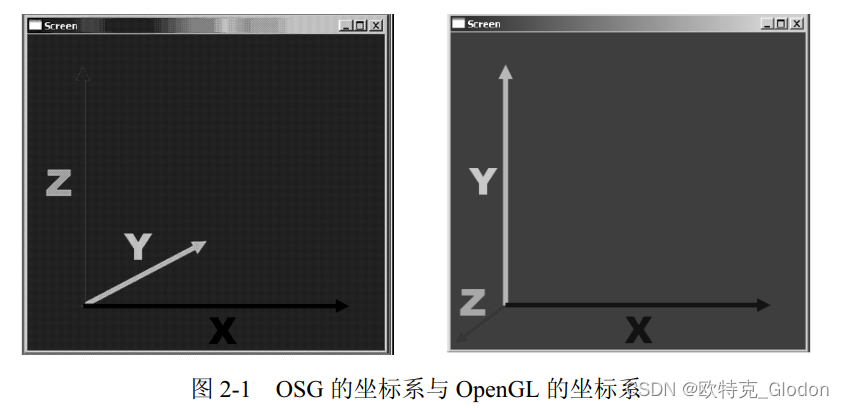
OSG：X 正方向向右，Y 正方向朝里，Z 正方向朝上。
OpenGL：X 正方向向右，Y 正方向朝上，Z 正方向朝外。

OSG 的坐标系统可以理解为 OpenGL 坐标系统绕 X 轴顺时针旋转 90°。读者需牢记并理解坐标系，以后经常会遇到按一定的要求进行图形变换的情况。图 2-1 形象地描述了两个坐标系，其中，左侧的为 OSG 的坐标系，右侧的为 OpenGL 的坐标系。
在这里插入图片描述

2、坐标系变换

坐标系变换是计算机图形处理的一个基础研究方向。三维实体对象需要经过一系列的坐标变换才能正确、真实地显示在屏幕上。在一个场景中，当读者对场景中的物体进行各种变换及相关操作时，坐标系变换是非常频繁的。坐标系变换通常包括世界坐标系-物体坐标系变换、物体坐标系-世界坐标系变换和世界坐标系-屏幕坐标系变换。屏幕坐标系是一个二维平面坐标系，即显示器平面，是非常标准的笛卡儿坐标系的第一象限区域。使用 OSG 开发时，经常会用到坐标系变换。下面介绍在 OSG 中坐标系变换的具体实现，可能不能面面俱到，但具有普遍应用性。

2.1 世界坐标系-物体坐标系变换

世界坐标系-物体坐标系变换相对比较容易，它描述的问题主要是关于物体本身的。假设在世界坐标系中，一个人正准备走向一栋建筑，那么他就面临世界坐标系到物体坐标系的变换过程，变换过程中面临的问题是人相对建筑物的朝向、人相对建筑物的距离及人的移动方向等一系列的问题。上面的假设读者或许会觉得非常熟悉，它基本等同于基本变换的过程。在 OSG 中，已有如下相关的类实现了基本变换过程：

osg::PositionAttitudeTransform //位置变换类
osg::MatrixTransform //矩阵变换类

这两个类实现的效果基本是相同的，只是数据的表达方式有区别，这样有利于处理各种数据的变换。后面的章节还会详细介绍，这里暂且留一个如何使用这两个类的疑问。或许学习这一章读者会有很多实现方面的疑问，不过没关系，通读全书后将不再疑惑。通过上面的两个类可以很方便地实现世界坐标系-物体坐标系的变换过程应该是容易理解的。世界坐标系-物体坐标系变换的意义在于简化了世界坐标系下变换的运算，当面对非常大的场景时，这种变换在一定程度上可以减少数据的运算量和提高场景的渲染效率。

2.2 物体坐标系-世界坐标系变换

物体坐标系-世界坐标系变换不能简单地理解为世界坐标系-物体坐标系变换的逆过程。物体坐标系-世界坐标系变换描述的问题是处于世界坐标系中的物体。假设在物体坐标系中，一栋建筑物中有一个人，如何确定人在世界坐标系中的位置信息就是物体坐标系-世界坐标系变换所面对的问题。物体坐标系-世界坐标系变换是有一定难度的。
对于场景图形中某一个 OSG 节点，它和根节点之间可能存在一些变换节点，那么如何获取该节点在世界坐标系中的位置就显得非常困难。但是，在场景图形中，每一个节点都有自己的父节点且有自己的变换矩阵，这些变换矩阵包含了相对坐标数据。那么，计算某一特定节点在世界坐标系下的坐标，只需要将该节点的根节点和该节点之间的所有变换矩阵相乘即可。
在 OSG 中有多种方式来实现物体坐标系-世界坐标系的变换，如回调、访问器等，用访问器实现是一种方便可操控的方式，相对而言，回调在一定程度上不具备可操控行，且会因为增加额外开销而影响渲染效率，但每帧都会自动计算矩阵变换。访问器通过遍历的方式记录场景中节点的路径，并计算路径上矩阵变换的世界坐标，最终返回一个矩形式表示的世界坐标。下面具体实现该访问器，读者不必理解每一行代码，但需要理解实现的基本思路和原理，在以后的学习中，读者将逐渐熟悉代码，这些代码会经常用到。

//该访问器类用于返回某个节点的世界坐标
//从起始节点开始向根节点遍历，并将遍历的节点记录到 nodePath 中
//第一次到达根节点之后，记录起始点到根节点的节点路径
//获取所有世界坐标矩阵之后，即获得节点的世界坐标
class GetWorldCoordinateOfNodeVisitor : public osg::NodeVisitor
{
public:
	GetWorldCoordinateOfNodeVisitor() :
		osg::NodeVisitor(NodeVisitor::TRAVERSE_PARENTS), done(false)
	{
		wcMatrix = new osg::Matrixd();
	}

	virtual void apply(osg::Node& node)
	{
		if (!done)
		{
			//到达根节点，此时节点路径也已记录完整
			if (0 == node.getNumParents())
			{
				wcMatrix->set(osg::computeLocalToWorld(this->getNodePath()));
				done = true;
			}
			//继续遍历
			traverse(node);
		}
	}
	//返回世界坐标矩阵
	osg::Matrixd* giveUpDaMat()
	{
		return wcMatrix;
	}
private:
	bool done;

	osg::Matrix* wcMatrix;
};

//计算场景中某个节点的世界坐标，返回 osg::Matrix 格式的世界坐标
//创建用于更新世界坐标矩阵的访问器之后，即获取该矩阵
osg::Matrixd* getWorldCoords(osg::Node* node)
{
	GetWorldCoordinateOfNodeVisitor* ncv = new GetWorldCoordinateOfNodeVisitor();

	if (node && ncv)
	{
		//启用访问器
		node->accept(*ncv);

		return ncv->giveUpDaMat();
	}
	else
	{
		return NULL;
	}
}

2.3 世界坐标系-屏幕坐标系变换

在场景中，所有的实体对象需要经过一系列的坐标变换才能正确显示在屏幕上，这些变换主要包括模型变换（将实体对象正确地放置在场景中）、投影变换（将场景中的实体对象投影到垂直于视线方向的二维成像平面上）和视口变换（投影变换之后得到的顶点需要经过视区变换才能得到最后的窗口坐标）。屏幕坐标是二维坐标，世界坐标是三维坐标，因此，正确的世界坐标系-屏幕坐标系变换就非常必要。
通过前面的介绍可知，世界坐标系-屏幕坐标系变换主要有 3 个步骤，即模型变换、投影变换和视口变换，由模型变换和投影变换得到归一化的设备坐标，最后由视口变换得到屏幕窗口坐标。

//返回三维点在二维屏幕上的投影点
osg::Vec3d WorldToScreen(osgViewer::View* view,osg::Vec3 worldpoint)
{
double in[4], out[4];

in[0] = worldpoint._v[0];
in[1] = worldpoint._v[1];
in[2] = worldpoint._v[2];
in[3] = 1.0;
//获得当前的投影矩阵和模型视图矩阵
osg::Matrix projectMatrix= view->getCamera()->getProjectionMatrix();
osg::Matrix viewprojectMatrix = view->getCamera()->getViewMatrix();
//变换模型视图矩阵
double modelViewMatrix[16];
memcpy(modelViewMatrix,viewprojectMatrix.ptr(),sizeof(GLdouble) * 16);
Transform_Point(out, modelViewMatrix, in);
//变换投影矩阵
double myprojectMatrix[16];
memcpy(myprojectMatrix,projectMatrix.ptr(),sizeof(GLdouble) * 16);
Transform_Point(in, myprojectMatrix, out);

//变换视口变换矩阵
if (in[3] == 0.0)
return osg::Vec3d(0,0,0);

in[0] /= in[3];
in[1] /= in[3];
in[2] /= in[3];

int viewPort[4];
osg::Viewport* myviewPort = view->getCamera()->getViewport();
viewPort[0] = myviewPort->x();
viewPort[1] = myviewPort->y();
viewPort[2] = myviewPort->width();
viewPort[3] = myviewPort->height();
//计算二维屏幕投影点
osg::Vec3d sceenPoint;
sceenPoint._v[0] = (int)(viewPort[0] + (1 + in[0]) * viewPort[2] / 2 + 0.5);
sceenPoint._v[1] = (int)(viewPort[1] + (1 + in[1]) * viewPort[3] / 2 + 0.5);
sceenPoint._v[2] = 0;

return sceenPoint;
}

//输入点，进行矩阵变换
void Transform_Point(double out[4], const double m[16], const double in[4])
{
#define M(row,col) m[col*4+row]
out[0] =M(0, 0) * in[0] + M(0, 1) * in[1] + M(0, 2) * in[2] + M(0,
) * in[3];
out[1] =M(1, 0) * in[0] + M(1, 1) * in[1] + M(1, 2) * in[2] + M(1,
) * in[3];
out[2] = M(2, 0) * in[0] + M(2, 1) * in[1] + M(2, 2) * in[2] + M(2,
) * in[3];
out[3] = M(3, 0) * in[0] + M(3, 1) * in[1] + M(3, 2) * in[2] + M(3,
) * in[3];
#undef M
}