这篇文章的标题涉及到以下关键概念：

1. 5G基站： 提到了5G基站，这表明文章的焦点可能是与第五代移动通信技术相关的内容。5G技术对于提高通信速度、降低延迟以及支持大规模连接等方面有显著的改进，因此对于基站的电力需求和供应可能存在新的挑战和机会。

2. 储能可调度容量： 提到了储能系统，并强调其可调度容量。这可能指的是在系统中引入了具有一定储能能力的设备，并且这些设备的储能量是可以进行调度和管理的。储能系统通常包括电池等技术，能够在需要时存储电能，以便在需要时释放。

3. 有源配电网： 文中提到了有源配电网，这表明讨论的是一种具备主动电源的配电网络。有源配电网相对于传统的被动电网，具有更灵活的能量管理能力，可以主动调整能量的产生和分配。

4. 协同优化调度方法： 这部分强调了文章的方法论，即采用协同优化调度方法。这可能涉及到对5G基站、储能设备和电网的协同管理和优化，以最大程度地提高系统效率和性能。

综合起来，这篇文章可能关注于在5G基站场景下，通过引入具有可调度储能容量的有源配电网，采用协同优化调度方法来解决相关的能源管理和优化问题。这样的研究对于提高基站的能效、稳定性和可持续性都具有实际意义。

摘要：随着移动通信向5G快速更新换代，5G基站建设规模快速增长，可将海量5G通信基站中的闲置储能视作灵活性资源参与电力系统调度，以减轻新能源发电的随机性和波动性对系统的不利影响。本文针对含分布式风力发电有源配电网的基站储能经济优化调度问题，首先计及配电网潜在电力中断以及停电恢复时间两个因素，建立基站可靠性评估模型，系统地评估各基站储能的实时可调度容量。进一步以最小化系统运行成本为目标，采用基于变分自编码器(variational auto-encoder，VAE)模型的改进双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic policy gradient，TD3)算法求解5G基站储能最优充放电策略。该算法将多基站储能状态用隐变量的形式表征以挖掘数据中隐含的关联，从而降低模型的求解复杂度，提升算法性能。通过迭代求解至收敛，实现多基站储能(Multi-base station energy storage，MBSES)系统的实时调控并为每个基站制定符合实际工况的个性化充放电策略。最后通过算例验证了所提方法的有效性。

这段摘要描述了一种面向包含分布式风力发电有源配电网的5G基站的储能经济优化调度方法。以下是对摘要的详细解读：

1. 5G基站建设规模快速增长： 摘要开头指出，随着移动通信向5G的快速更新换代，5G基站的建设规模正在迅速增加。这表明5G基站在电力系统中的角色变得越来越重要。

2. 储能作为灵活性资源： 提到了将5G通信基站中的闲置储能视作灵活性资源，参与电力系统调度。这意味着文章关注如何充分利用基站内的储能，在电力系统中发挥更为灵活的作用。

3. 针对分布式风力发电有源配电网： 研究的对象是含有分布式风力发电的有源配电网，这意味着考虑到了分布式可再生能源，其中风力发电可能具有不确定性和波动性。

4. 可靠性评估模型： 为解决基站储能的经济优化调度问题，文中建立了基站可靠性评估模型，考虑了配电网潜在电力中断以及停电恢复时间两个因素。

5. 最小化系统运行成本： 研究的目标是最小化系统运行成本，这表明优化的方向是在保障系统可靠性的前提下，寻找储能的最优充放电策略。

6. 采用深度学习算法： 为解决最优充放电策略，文中采用了基于变分自编码器(VAE)模型的改进双延迟深度确定性策略梯度(TD3)算法。这些算法属于深度学习领域，用于处理复杂的非线性系统。

7. 隐变量降低模型复杂度： 算法引入了隐变量来表征多基站储能状态，以挖掘数据中的隐含关联，从而降低模型的求解复杂度，提升算法性能。

8. 实时调控和个性化策略： 通过迭代求解至收敛，实现了多基站储能系统的实时调控，并为每个基站制定符合实际工况的个性化充放电策略。

9. 算例验证： 最后，通过算例验证了所提方法的有效性，这意味着提出的方法在实际场景中是可行且有效的。

总体来说，这篇文章关注于在5G基站背景下，通过储能优化调度来应对分布式风力发电的波动性，使用深度学习算法提高系统性能，最终通过案例验证了方法的可行性和有效性。

关键词: 5G基站; 备用储能;可再生能源;可调度容量: 特征编码;深度强化学习;

1. 5G基站： 指的是第五代移动通信技术的基站。在这个上下文中，可能涉及到5G基站的快速建设和更新换代。

2. 备用储能： 意味着基站具备一种备用的储能系统，通常是电池或其他形式的储能设备，用于应对电力系统中的不确定性和波动性。

3. 可再生能源： 指的是通过自然过程生成的能源，如太阳能、风能等。在这里，可能是指分布式风力发电等可再生能源的整合和利用。

4. 可调度容量： 表示储能系统中可以实时调度使用的电能容量。这可能涉及到储能系统的实时管理，以最大限度地提高系统的灵活性。

5. 特征编码： 涉及到将数据或系统的特征以某种方式进行编码，可能是为了简化问题、降低维度，或者更有效地表征数据的关键特征。在这里，可能是使用特征编码来处理多基站储能状态的复杂性。

6. 深度强化学习： 是一种结合了深度学习和强化学习的方法。在这个上下文中，可能是指使用深度强化学习算法，如基于变分自编码器(VAE)模型的改进双延迟深度确定性策略梯度(TD3)算法，来解决储能系统的最优控制问题。深度强化学习可以处理复杂、非线性的系统，并通过学习来优化控制策略。

仿真算例：本文以改进 IEEE33 节点配电系统作为算例仿真原型。如图 2 所示，在节点 14 设置一台分布式风力发电机组，装机容量为 3MW；在节点 9～18以及 28～33 共计 16 个节点处设立含储能的 5G 基站，每个节点下设立 4 台 5G 基站，各节点下的基站负载随机选择，基站备用储能电池选择梯次利用的磷酸铁锂电池。单个基站的设备参数如附录D 表 D1 所示。本文采用 Elia.be 对 Aggregate Belgian Wind Farms 地区在 01/06/2021-20/06/2021期间的风电出力曲线数据预测以及负荷数据[36]作为训练集。以该地区在 20/06/2021-30/06/2021 期间的运行数据作为测试集以验证调度决策效果，出力曲线如附录 D 图 D2 和 D3 所示。以上数据均乘以适当的比例系数以适应配电系统容量。本实验以 Tensorflow2.0 为框架，编程环境为Pythoon3.8，模型在一套配有 AMD Ryzen7 4800H CPU@2.90GHz 及一张 NVIDIA GeForce RTX2060显卡的机器上实现。网络训练分为 VAE 模型的特征编码和 VAE-TD3 算法优化调度两个部分。VAE模型训练的训练回合数为 1000，学习率为 0.001，batch_size 设置为 128，隐变量维度设置为 32，具体网络结构见附录 D 表 D4 所示；VAE-TD3 网络训练参数见附录 D 表 D5 所示。

仿真程序复现思路：

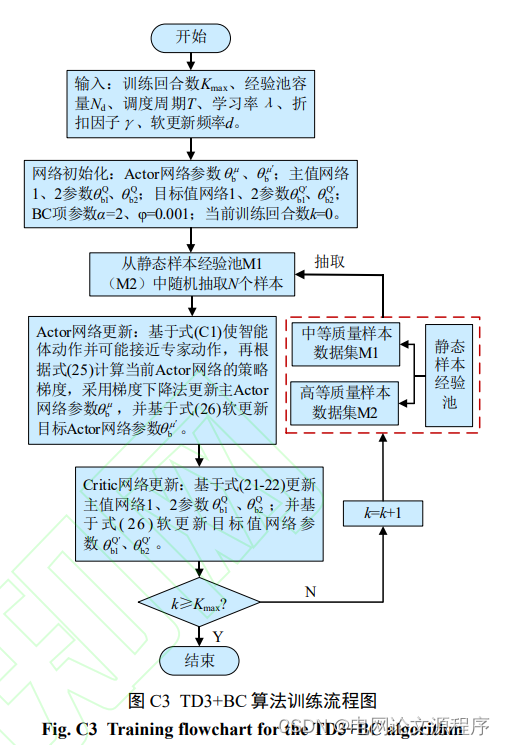
由于问题的复杂性，以下是一个简化版本的代码示例，以说明如何使用TensorFlow 2.0和Python 3.8实现仿真程序的关键部分。请注意，实际实现可能需要更多的细节和调整以适应具体的问题。

import tensorflow as tf
import numpy as np
import networkx as nx
from tensorflow.keras.layers import Input, Dense, Concatenate
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam

# 步骤1: 数据准备
# 数据处理略，假设已经有了预处理好的数据

# 步骤2: 搭建仿真模型
# 创建 IEEE33 节点配电系统结构，设置基站参数和风力发电机组
G = nx.Graph()
# 添加节点、边等...

# 步骤3: 模型训练
# 3.1 VAE模型的特征编码训练
def build_vae_model(input_dim, latent_dim):
    inputs = Input(shape=(input_dim,))
    encoder = Dense(64, activation='relu')(inputs)
    z_mean = Dense(latent_dim)(encoder)
    z_log_var = Dense(latent_dim)(encoder)

    def sampling(args):
        z_mean, z_log_var = args
        batch = tf.shape(z_mean)[0]
        dim = tf.shape(z_mean)[1]
        epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
        return z_mean + tf.exp(0.5 * z_log_var) * epsilon

    z = tf.keras.layers.Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
    encoder = Model(inputs, [z_mean, z_log_var, z])

    decoder_h = Dense(64, activation='relu')
    decoder_mean = Dense(input_dim, activation='sigmoid')
    h_decoded = decoder_h(z)
    x_decoded_mean = decoder_mean(h_decoded)
    vae = Model(inputs, x_decoded_mean)

    return vae

input_dim =  # 根据你的数据维度设置
latent_dim = 32  # 根据你的需求设置
vae_model = build_vae_model(input_dim, latent_dim)
vae_model.compile(optimizer=Adam(learning_rate=0.001), loss='mse')
vae_model.fit(training_data, epochs=1000, batch_size=128)

# 3.2 VAE-TD3算法优化调度训练
def build_vae_td3_model(input_dim, action_dim):
    wind_input = Input(shape=(input_dim,))
    load_input = Input(shape=(input_dim,))
    concatenated_input = Concatenate()([wind_input, load_input])

    # 假设有一些神经网络层用于调度决策
    # 这里只是一个简单的例子，实际情况需要更复杂的网络结构
    # 请根据具体问题进行调整
    x = Dense(64, activation='relu')(concatenated_input)
    x = Dense(32, activation='relu')(x)
    output = Dense(action_dim, activation='tanh')(x)

    vae_td3_model = Model(inputs=[wind_input, load_input], outputs=output)
    return vae_td3_model

action_dim =  # 根据你的问题设置
vae_td3_model = build_vae_td3_model(input_dim, action_dim)
vae_td3_model.compile(optimizer=Adam(learning_rate=0.001), loss='mse')
vae_td3_model.fit(training_data, epochs=num_epochs, batch_size=batch_size)

# 步骤4: 仿真运行
# 4.1 输入风电和负荷数据
wind_data, load_data = preprocess_data(test_data)

# 4.2 运行调度算法
schedule_decisions = vae_td3_model.predict([wind_data, load_data])

# 步骤5: 结果验证
# 5.1 与测试集比较
compare_results(schedule_decisions, test_results)

这个例子中的代码是一个简化的版本，实际的实现可能会根据具体问题的要求进行更多的调整和优化。请确保根据需求适当修改模型结构、参数和训练过程。