leedcode 刷题 - 除自身以外数组的乘积

I238. 除自身以外数组的乘积 - 力扣（LeetCode）

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
 

提示：

2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内
 

进阶：你可以在 O(1) 的额外空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组 不被视为 额外空间。）

题目已经给的很明显了，就是使用前缀积和后缀积的方式来求解，这种方式其实是一个简化的动态规划。

用两个数组，分别存储从起始位置到 i 位置的乘积和从末尾位置到 i 位置的乘积；

上述两个结果对应的就是 f[i] 和 g[i] 。

递推公式：

f[i] = f[i - 1] * nums[i - 1];

g[i] = g[i + 1] * nums[i + 1];

f[0] 和 g[nums.size()] 都是需要自己手动算的，上述递推公式是算不出来的。

如果我们像计算题目描述的某个位置（比如是 i 位置）的前缀积和后缀积的话，只需要计算 f[i] * g[i] 既可，因为 f[i] 表示的就是 i 之前的所有积，g[i] 表示的就是 i 之后的所有的积。

完整代码：

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> f(nums.size(), 1);
        vector<int> g(nums.size(), 1);
        vector<int> ret(nums.size());

        for(int i = 1;i < nums.size(); i++) f[i] = f[i - 1] * nums[i - 1];
        for(int i = nums.size() - 2; i >= 0; i--) g[i] = g[i + 1] * nums[i + 1];
        for(int i = 0;i < nums.size();i++) ret[i] = g[i] * f[i];

        return ret;
}
};

I560. 和为 K 的子数组 - 力扣（LeetCode）

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

示例 1：

输入：nums = [1,1,1], k = 2
输出：2
示例 2：

输入：nums = [1,2,3], k = 3
输出：2

还是使用前缀和，我们可以使用找到一个前缀和 sum[i] 就表示，从数组 0 号位置开始，到 i 位置的所有元素之和。

那么，我们只需要在这个区间当中找到在 [0,i] 这个区间当中,某一个位置作为起始位置（假设为 j ），到 i 位置，这个子数组的元素之和等于k，那么，[0,j] 这个区间当中各个元素之和就是 sum[i] - k;

往后，只需要 i 往后寻找，就不会找漏。

但是，上述还是有一个问题，如果我们直接遍历 sum 数组的，来找到 j 这个位置的话，在加上创建 sum 数组的时间复杂度，实际上，这个算法的整个时间复杂度其实还不如暴力解法。

所以，其实我们不用循环一个一个去找 j 位置，我们可以利用一个 hash 表来代替 sum 存储的这些前缀和的值，也就是代替 sum 存储其中的每一个元素。

哈希表： hash<前缀和值，前缀和出现次数>

这样，如果我们想在 [0,i] 这个区间当中, 找到 j 这个位置，只需要利用 hash 表的快速查找来查找在当前hash 表当中有没有 sum[i] - k 这个前缀和，同时，利用 hash 表当中的 count（）函数，可以快速查找，这个 sum[i] - k 出现次数。

关于前缀和加入hash 表的时机：
因为我们的前缀和算法，是要找的是在 [0,i] 这个区间当中，有多少个前缀和等于sum[i] - k; 。

如果直接在一开始就把 sum 计算出来，然后把区间当中前缀和和前缀和出现的次数加入到 hash 表当中是会计算到 i 后面的值。所以不行。

所以，我们在计算 i 位置之前，哈希表里面值存储 [0, i - 1] 位置的前缀和。

还有一种情况，当当前的整个的前缀和等于 k 的话，那么，在上述的算法当中，其实我们是找不到这个情况的，因为我们找到的是等于 k 的子区间，这个子区间的起始位置上述说过了，是 j ，那么满足 sum[i] - k; 的区间就是 [0, j - 1]，那么在这个情况当中就是 [0, -1] 这个区间，这个区间是不存在的。

所以，我们开始就要默认数组当中有一个和为 0 的前缀和，即： hash[0] = 1;

完整代码：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> hash(nums.size());
        hash[0] = 1;

        int sum = 0, ret = 0; // sum 代替sum数组，利用变量给 hash 当中赋值；ret 返回个数
        for(auto& e : nums)
        {
            sum += e; // 计算当前的前缀和

            // 计算满足 条件的区间，是否在 hash 当中出现。count（）函数判断是否出现
            //  出现计数器 加上 这个前缀和 在 hash 当中出现的次数
            if(hash.count(sum - k)) ret += hash[sum - k]; 
            hash[sum]++;                  
        }

        return ret;
    }
};

I974. 和可被 K 整除的子数组 - 力扣（LeetCode）

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目。

子数组 是数组的连续部分。

示例 1：

输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:

输入: nums = [5], k = 9
输出: 0

要解决这道题目，首先要知道同于定理

也就是 如果 a 和 b 的差值，除上 p ，如果是整除的话，也就是余数是零的话，a 除上 p 的余数 = b 除上 p 的余数。

而且，还需要清楚，在C++ 当中， [负数 % 正数] 的结果是一个负数。

也就是说，其实[负数 % 正数] 其实结果也是一个余数，但是这个余数是负数。

所以，针对这种情况，我们要对这个负数进行修正，把他修正为正数。

所以，当我们在计算 [负数 % 正数] 的结果之时，其实，计算出的负数的结果在加上模数（也就是其中的正数），其实就是对应的正数的结果。如下图所示：

上述的计算方式对于 a 是负数的情况来说，计算出的结果就是修正之后的结果，也就是修正为正数之后的结果。

但是上述的修正方式对于 a 是正数的情况是计算错误的，因为对于 a 是正数的情况来说， a % b 本来就是正确的结果，但是后面又加上了一个 b，所以是不正确的。

所以，为了正数和负数统一，我们共用的方式就是在上述计算式子当中，再 % b 即可。

上述式子就是我们想要的i修正公式了。

所以，按照和这个问题其实就和上述和为K的子数组求解方式一样了。

先求出所有的从 0 号数组位置开始的所以前缀模，保存到一个数组当中，然后求出与 K 模的余数即可。

同样优化方式和上述一样，不需要多定义一个数组来保存前缀模，这样也不好查找对应的前缀模，只需要用一个 hash表来存储即可。

上述问题就被简化为了在 [0, i - 1] 这个区间当中，找到有多少个前缀和的余数等于 (sum % k + k ) % k。

完整代码：

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int, int> hash;
        hash[0 % k] = 1; // 0 这数的余数

        int sum = 0, ret = 0;
        for(auto& e : nums)
        {
            sum += e;
            int r = (sum%k + k) % k;
            if(hash.count(r)) ret += hash[r];
            hash[r]++;
        }
        return ret;
    }
};

I525. 连续数组 - 力扣（LeetCode）

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

示例 1:

输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:

输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

在数组当中，所有的元素的值要么是 0 ，要么是1。我们需要找到一个符合要求的最长的连续的子数组，返回这个子数组的长度。

我们在统计个数的时候，其实是可以做到转化的，如果把 0 全部替换为-1，那么我们统计个数的问题，其实就转化成了找到一个元素之和等于 0 的子数组。

所以，这道题目就可以使用前缀和的方法来解决。

使用hash 表来存储前缀和为 sum 的区间，所以吗，应该是 unordered_map<sum, i > （其中 sum 是前缀和，i 是这个前缀和区间的下标）。

当找到某一个下标，和为 sum，计算出这个区间的长度，就把这个对应的绑定的值存入到哈希表当中。

如果有重复的 sum，但是区间不一样，不需要重新更新原本在 hash 表当中的 <sum , i>，只需要保留之前存入的 <sum, i> 即可。因为，我们需要找到子区间最长的子数组，那么下标应该是越考左，那么计算出的子区间长度才是最大的。

同样，为了处理特殊情况：当 [0 , i] 这个子区间计算出的前缀和就是0了，那么按照上述和为K的子数组这个题目当中逻辑去找到子区间的话，就会在 -1 为开始的区间去找。

所以，我们需要在开始默认一个子区间的前缀和是0，即 hash[0] = -1;

上述的过程就可以找出所有的合法的子数组了，现在就是如何计算这个子数组的区间大小？

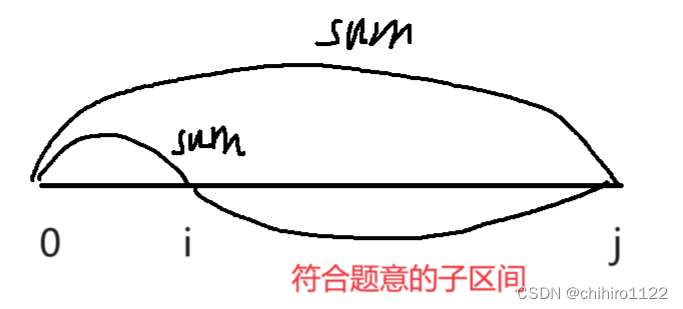
如上，我们只需要找出 i 和 j 两个下标，使得 [0, i] 的前缀和和 [0, j] 的前缀和相等即可。

所以我们计算出的区间的长度就是 i - j 。

完整代码：

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        unordered_map<int ,int> hash;
        hash[0] = -1;   // 默认 刚开始 哈希表当中有一个 前缀和为0 的区间

        int sum = 0, ret = 0;
        for(int i = 0 ;i < nums.size(); i++)
        {
            sum += nums[i] == 0 ? -1 : 1; // 如果是 0 就加-1，如是1 就加 1

            // 如果 sum 在hash 当中存在，说明此时就已经找到了 符合条件的子区间
            // 那么就更新的 ret 返回值。
            if(hash.count(sum)) ret = max(ret, i - hash[sum] + 1 - 1);
            else hash[sum] = i;  // sum 在 hash 当中不存在，那么 就添加一个 hash 元素
        }

        return ret;
    }
};