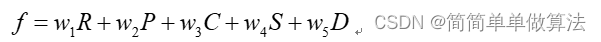目录
- 1 二叉树的顺序结构
- 2. 堆的概念及结构
- 3 .堆的实现(小堆)
1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段
2. 堆的概念及结构
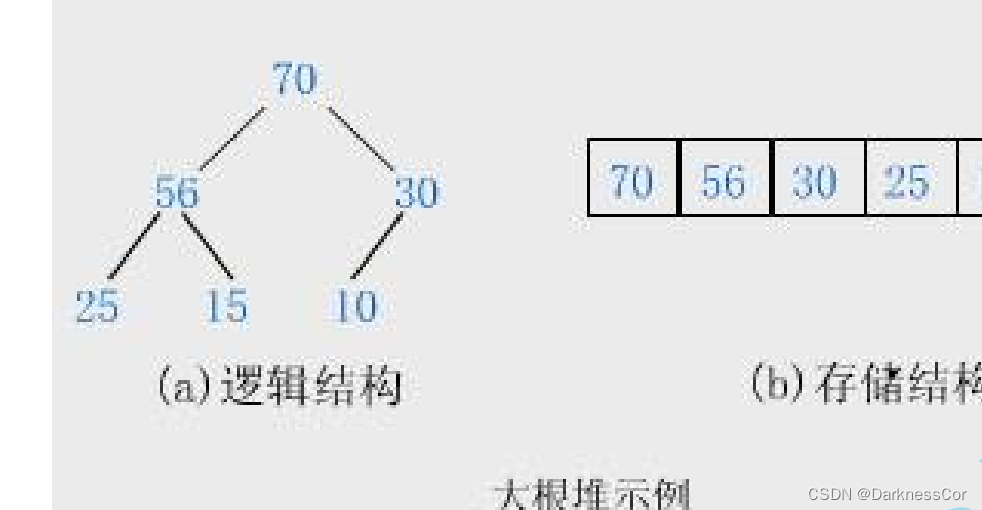
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,
2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。
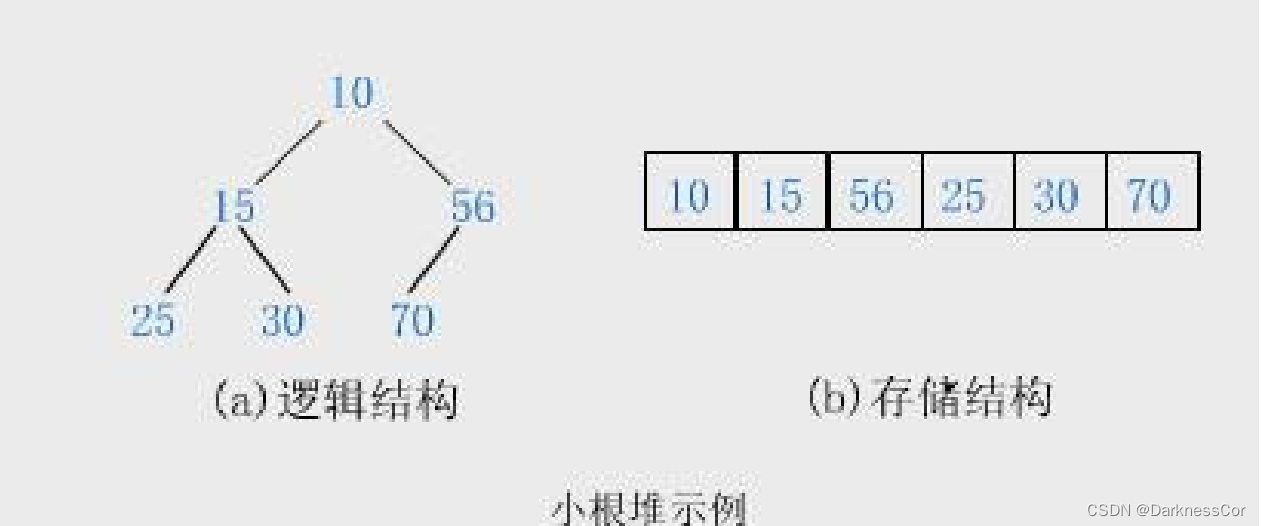
3 .堆的实现(小堆)
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
int* a;
int size;
int capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
// 规定删除堆顶(根节点)
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
size_t HeapSize(HP* php);
bool HeapEmpty(HP* php);
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
int parent =(child - 1 )/ 2;
while (child > 0)
{
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void AdjustDown(HPDataType* a, int size,int parent)
{
int child = parent * 2 + 1;
while (child<size)
{
if (child+1<size&&a[child + 1] < a[child])
{
child++;
}
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void HeapInit(HP* php)
{
php->a = NULL;
php->capacity = 0;
php->size = 0;
}
void HeapDestroy(HP* php)
{
free(php->a);
free(php);
}
HPDataType HeapTop(HP* php)
{
return php->a[0];
}
size_t HeapSize(HP* php)
{
return php->size;
}
bool HeapEmpty(HP* php)
{
return php->size == 0;
}
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->capacity == php->size)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size++] = x;
AdjustUp(php->a, php->size-1);
}
void HeapPop(HP* php)
{
assert(php);
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
int parent = 0;
AdjustDown(php->a, php->size, 0);
}
堆的建立有两个重要算法即向上调整和向下调整法
堆向下调整算法:现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整 成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整
向上调整法:
向上调整算法,直到满足堆。
结尾:今天的分享到此结束,喜欢的朋友如果感觉有帮助可以点赞三连支持,咱们共同进步!