文章目录
- 计数排序+桶排序+基数排序
- 一、计数排序
- 概念:
- 写法一:
- 写法二:
- 二、桶排序
- 概念
- 代码
- 三、基数排序
- 概念
- 1.LSD排序法(最低位优先法)
- 2.MSD排序法(最高位优先法)
- 基数排序VS基数排序VS桶排序
计数排序+桶排序+基数排序
一、计数排序

- 时间复杂度:
- 空间复杂度:
- 稳定性:稳定
概念:
-
非基于比较的排序
-
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用
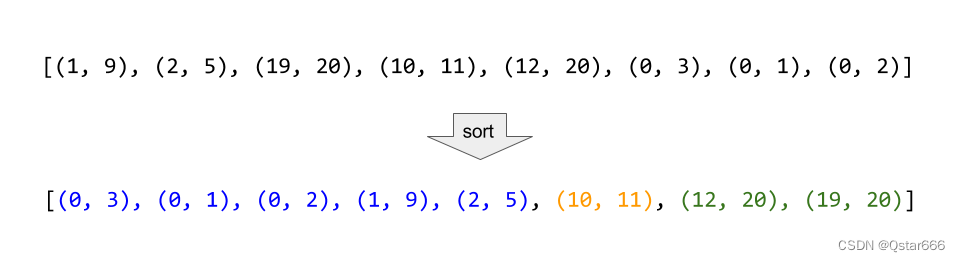
1.统计相同元素出现的个数
2.根据统计的结果将序列回收到原来的序列中
-
计数排序使用的场景:给出指定范围内的数据进行排序
-
使用场景:一组集中在某个范围内的数据
写法一:
- 通过遍历计数数组,循环输出计数数组存的次数
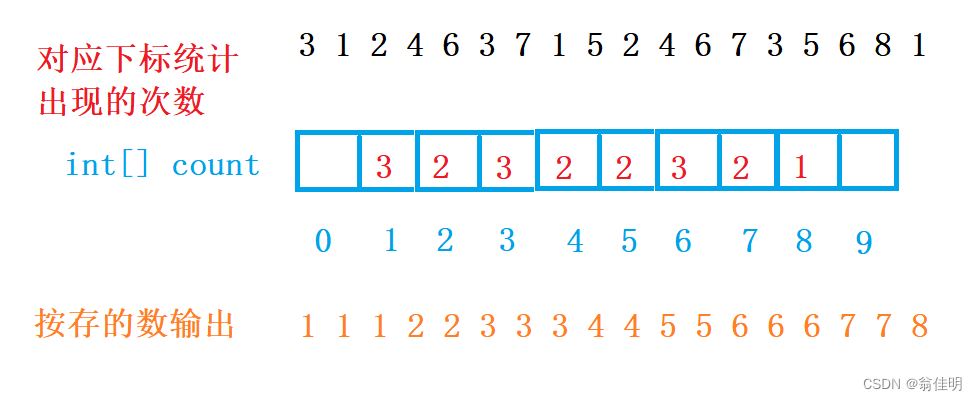
- 1.遍历数组找到最小值最大值
- 2.根据最大最小值,申请一个计数数组
- 3.遍历待排数组进行计数
- 4.遍历计数数组进行输出
/**
* 计数排序
*无法保证稳定
* @param array
*/
public static void countSort2(int[] array) {
//1.遍历数组找到最大值和最小值
int MAX = array[0];
int MIN = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > MAX) {
MAX = array[i];
}
if (array[i] < MIN) {
MIN = array[i];
}
}
//2.根据最大最小值,申请一个计数数组
int len = MAX - MIN + 1;//长度
int[] count = new int[len];
//3. 遍历待排数组进行计数
for (int i = 0; i < array.length; i++) {
count[array[i] - MIN]++;
}
//4.遍历计数数组进行输出
int index = 0;//array数组新的下标
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
array[index] = i + MIN;//+最小值,求出真正的数
count[i]--;
index++;
}
}
}
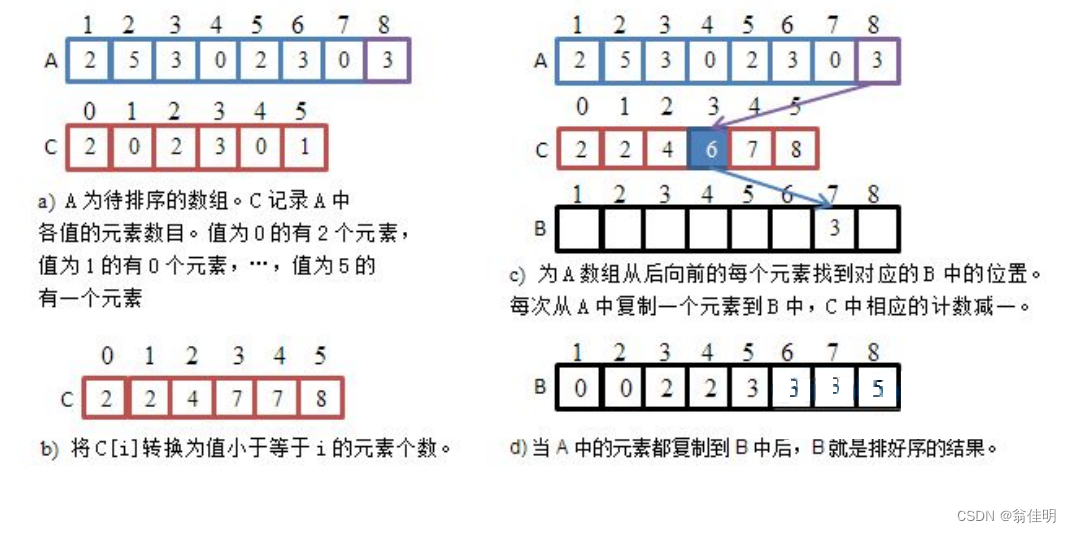
写法二:
- 写定数组的大小,用临时数组存储结构
- 计算每个元素在排序后的数组中的最终位置
- 根据计数数组将元素放到临时数组b中,实现排序
- 从后往前,根据原来数组的内容,在计数数组中找到要填写在b数组中的位置,
- 计数数组记录的不再是数字出现是次数,而是应该在数组中存放的位置下标
/**
* 计数排序
*稳定
* @param array
*/
public static void countSort(int[] array) {
int len = array.length;
final int MAX = 256;//常量确定数组大小
int[] c = new int[MAX];//计数数组
int[] b = new int[MAX];//临时数组,存放结果
//统计每个元素的出现次,进行计数
for (int i = 0; i < len; i++) {
c[array[i]]++;// 将a[i]作为索引,对应计数数组c中的位置加1
}
// 计算每个元素在排序后的数组中的最终位置
for (int i = 1; i < MAX; i++) {
c[i] += c[i - 1];// 计数数组中每个元素的值等于它前面所有元素的值之和
}
// 根据计数数组将元素放到临时数组b中,实现排序
for (int i = len - 1; i >= 0; i--) {
b[c[array[i]] - 1] = array[i];// 将a[i]放入临时数组b中的正确位置
c[array[i]]--;// 对应计数数组c中的位置减1,确保相同元素能够放在正确的位置
}
// 将临时数组b中的元素复制回原数组a,完成排序
for (int i = 0; i < len; i++) {
array[i] = b[i];
}
}
二、桶排序
概念
划分多个范围相同的区间,每个子区间自排序,最后合并
-
桶排序是计数排序的扩展版本,计数排序:每个桶只存储单一键值
-
桶排序: 每个桶存储一定范围的数值,确定桶的个数和范围
-
将待排序数组中的元素映射到各个对应的桶中,对每个桶进行排序
-
最后将非空桶中的元素逐个放入原序列中

代码
public static void bucketSort(int[] array){
// 计算最大值与最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < array.length; i++){
max = Math.max(max, array[i]);
min = Math.min(min, array[i]);
}
// 计算桶的数量
int bucketNum = (max - min) / array.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
// 将每个元素放入桶
for(int i = 0; i < array.length; i++){
int num = (array[i] - min) / (array.length);
bucketArr.get(num).add(array[i]);
}
// 对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
// 将桶中的元素赋值到原序列
int index = 0;
for(int i = 0; i < bucketArr.size(); i++){
for(int j = 0; j < bucketArr.get(i).size(); j++){
array[index++] = bucketArr.get(i).get(j);
}
}
}
三、基数排序
概念
-
基数排序是一种非比较型整数排序算法
-
将整数按位数切割成不同的数字,然后按每个位数分别比较
-
使用场景:按位分割进行排序,适用于大数据范围排序,打破了计数排序的限制
-
稳定性:稳定
-
按位分割技巧:arr[i] / digit % 10,其中digit为10^n。
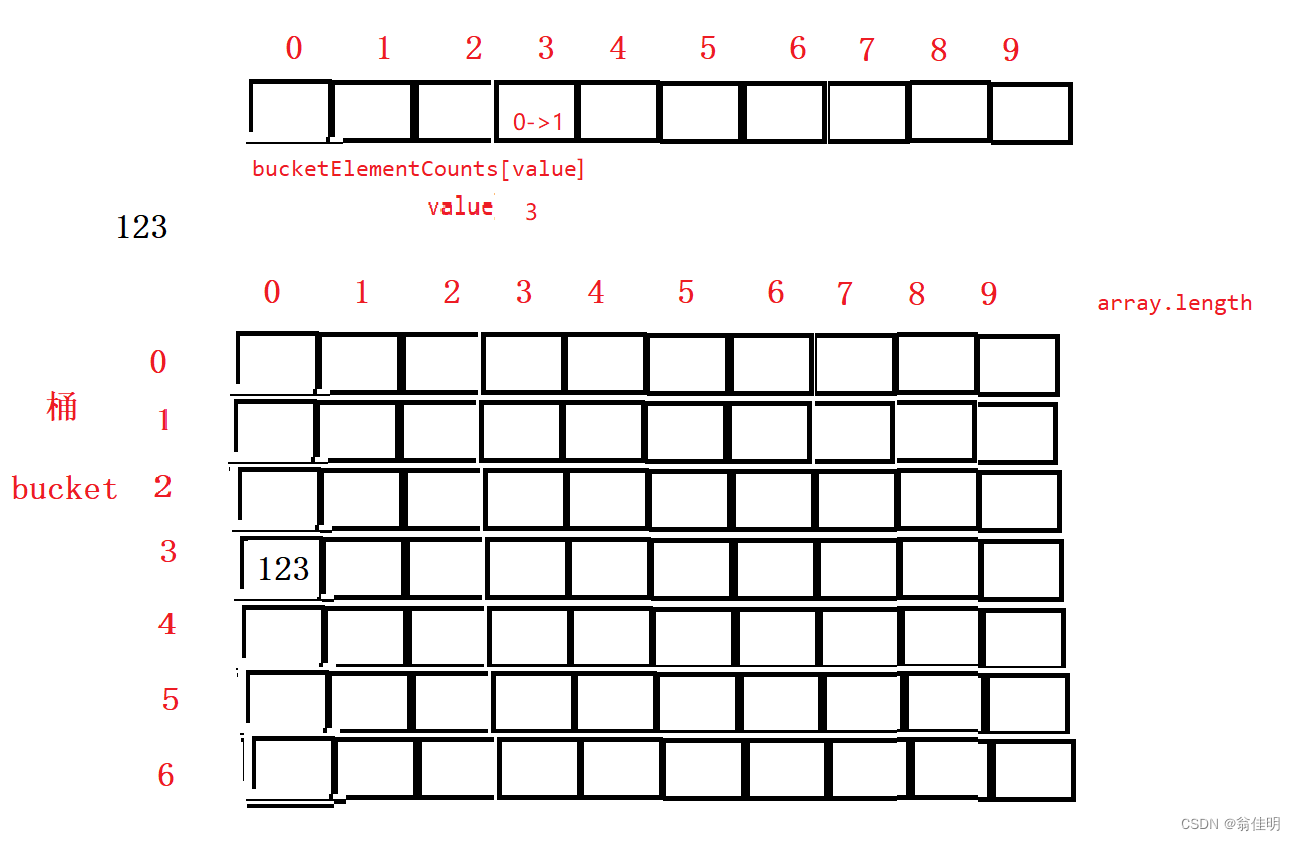
1.LSD排序法(最低位优先法)
-
从最低位向最高位依次按位进行计数排序。
-
进出的次数和最大值的位数有关
-
桶可以用队列来表示
-
数组的每个元素都是队列

- 1.先遍历找到最大值
- 2.求出最高位
public static void radixSortR(int[] array) {
//10进制数,有10个桶,每个桶最多存array.length个数
int[][] bucket = new int[10][array.length];
//桶里面要存的具体数值
int[] bucketElementCounts = new int[10];
//用来计算,统计每个桶所存的元素的个数,每个桶对应一个元素
//1.求出最大数
int MAX = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > MAX) {
MAX = array[i];
}
}
//求最大值的位数,先变成字符串,求字符串长度
int MAXCount = (MAX + "").length();
//最大位数的个数,进行几次计数排序
for (int i = 0; i < MAXCount; i++) {//i代表第几次排序
//放进桶中
for (int k = 0; k < array.length; k++) {
//k相当于遍历待排数值
//array[k] /(int) Math.pow(10, i)%10 求出每次要比较位的数
//求的是个位,并且是对应趟数的个位
int value = (array[k] / (int) Math.pow(10, i)) % 10;
//根据求出的位数,找到对应桶,放到对应桶的位置
bucket[value][bucketElementCounts[value]] = array[k];
//不管value 为多少,bucketElementCounts[value]的值都为0
//相当于存到对应桶的0位bucket[value][0]
bucketElementCounts[value]++; //从0->1
//对应桶的技术数组开始计数
}
//取出每个桶中的元素,赋值给数组
int index = 0;//array新的下标
for (int k = 0; k < bucketElementCounts.length; k++) {//遍历每个桶
if (bucketElementCounts[k] != 0) {//桶里有元素
for (int j = 0; j < bucketElementCounts[k]; j++) {//比那里每个桶的元素
array[index] = bucket[k][j];
index++;
}
}
bucketElementCounts[k] =0;//每个桶遍历完后,清空每个桶的元素;
}
}
}
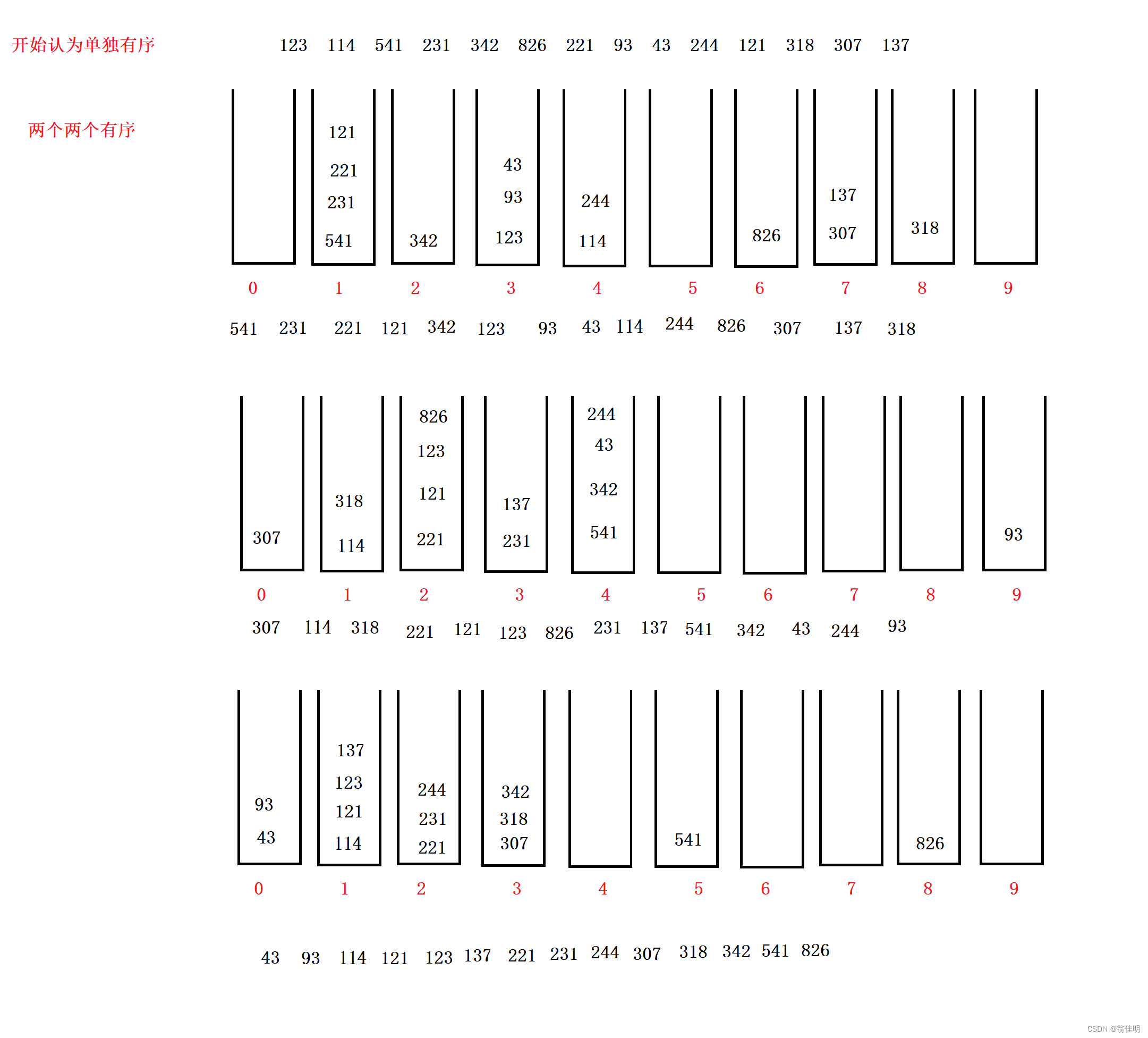
2.MSD排序法(最高位优先法)
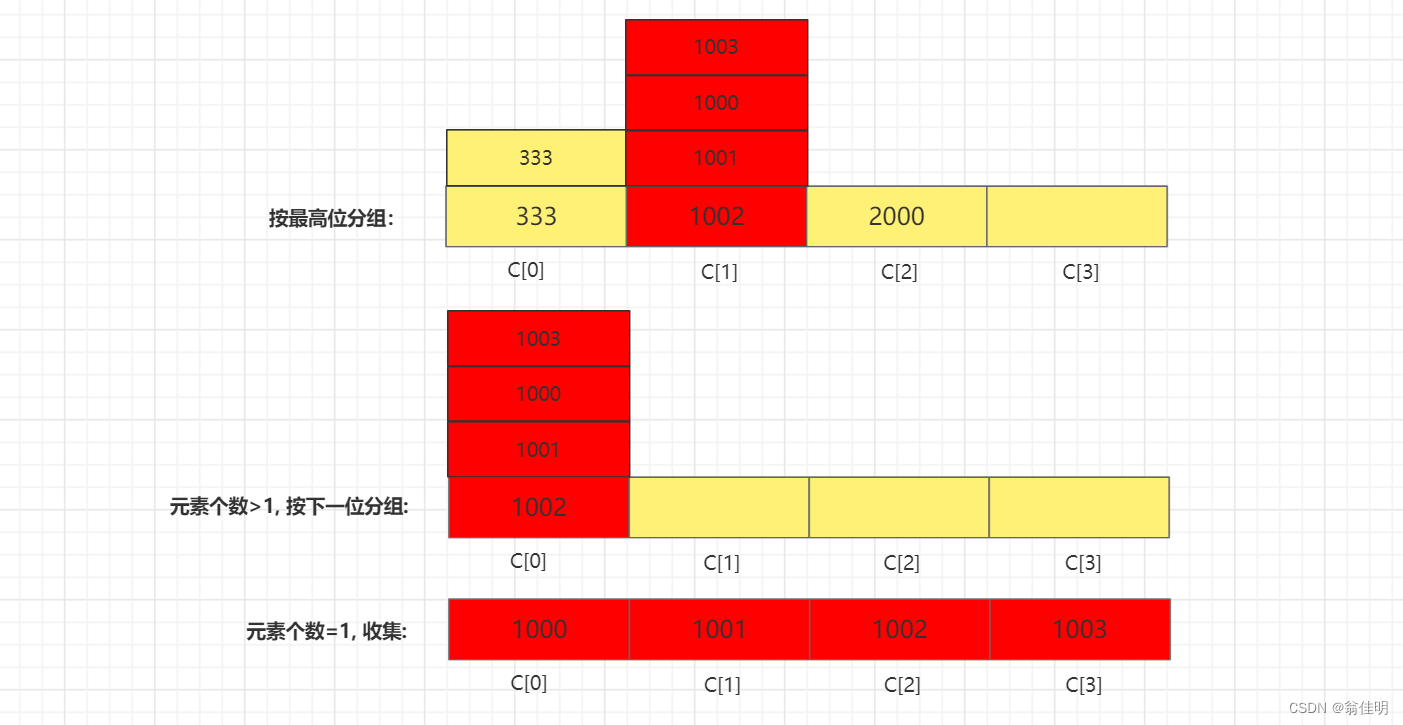
- 从最高位向最低位依次按位进行排序。
- 按位递归分组收集
- 1.查询最大值,获取最高位的基数
- 2.按位分组,存入桶中
- 3.组内元素数量>1,下一位递归分组
- 4.组内元素数量=1.收集元素
/**
* 基数排序--MSD--递归
* @param array
*/
public static void radixSortMSD(int[] array) {
//1.求出最大数
int MAX = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > MAX) {
MAX = array[i];
}
}
//求最大值的位数,先变成字符串,求字符串长度
int MAXCount = (MAX + "").length();
// 计算最大值的基数
int radix = new Double(Math.pow(10, MAXCount - 1)).intValue();
int[] arr = msdSort(array, radix);
System.out.println(Arrays.toString(arr));
}
public static int[] msdSort(int[] arr, int radix){
// 递归分组到个位,退出
if (radix <= 0) {
return arr;
}
// 分组计数器
int[] groupCounter = new int[10];
// 分组桶
int[][] groupBucket = new int[10][arr.length];
for (int i = 0; i < arr.length; i++) {
// 找分组桶位置
int position = arr[i] / radix % 10;
// 将元素存入分组
groupBucket[position][groupCounter[position]] = arr[i];
// 当前分组计数加1
groupCounter[position]++;
}
int index = 0;
int[] sortArr = new int[arr.length];
// 遍历分组计数器
for (int i = 0; i < groupCounter.length; i++) {
// 组内元素数量>1,递归分组
if (groupCounter[i] > 1) {
int[] copyArr = Arrays.copyOf(groupBucket[i], groupCounter[i]);
// 递归分组
int[] tmp = msdSort(copyArr, radix / 10);
// 收集递归分组后的元素
for (int j = 0; j < tmp.length; j++) {
sortArr[index++] = tmp[j];
}
} else if (groupCounter[i] == 1) {
// 收集组内元素数量=1的元素
sortArr[index++] = groupBucket[i][0];
}
}
return sortArr;
}
基数排序VS基数排序VS桶排序
-
都是非比较型排序
-
三种排序算法都利用了桶的概念
1.计数排序:每个桶只存储单一键值;
2.基数排序:根据键值的每位数字来分配桶
3.桶排序: 每个桶存储一定范围的数值;
点击移步博客主页,欢迎光临~