合并区间-力扣算法题56题
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
java实现算法代码
class Solution {
public int[][] merge(int[][] intervals) {
if (intervals.length == 0) {
return new int[0][2];
}
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] interval1, int[] interval2) {
return interval1[0] - interval2[0];
}
});
List<int[]> merged = new ArrayList<int[]>();
for (int i = 0; i < intervals.length; ++i) {
int L = intervals[i][0], R = intervals[i][1];
if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
merged.add(new int[]{L, R});
} else {
merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
}
}
return merged.toArray(new int[merged.size()][]);
}
}
算法思路(力扣的思路)
如果我们按照区间的左端点排序,那么在排完序的列表中,可以合并的区间一定是连续的。如下图所示,标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间,它们在排完序的列表中是连续的: 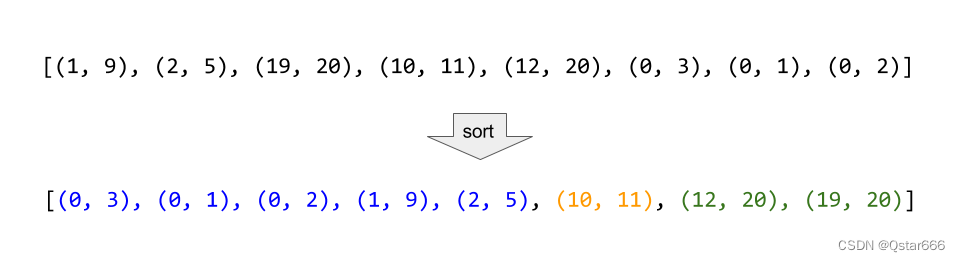
算法
我们用数组 merged 存储最终的答案。
首先,我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入 merged 数组中,并按顺序依次考虑之后的每个区间:
如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后,那么它们不会重合,我们可以直接将这个区间加入数组 merged 的末尾;
否则,它们重合,我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点,将其置为二者的较大值。
正确性证明
上述算法的正确性可以用反证法来证明:在排完序后的数组中,两个本应合并的区间没能被合并,那么说明存在这样的三元组 (i,j,k) 以及数组中的三个区间 a[i],a[j],a[k] 满足 i<j<k 并且 (a[i],a[k])可以合并,但 (a[i],a[j]) 和 (a[j],a[k]) 不能合并。这说明它们满足下面的不等式:
a[i].end<a[j].start(a[i] 和 a[j] 不能合并)a[j].end<a[k].start(a[j] 和 a[k] 不能合并)a[i].end≥a[k].start(a[i] 和 a[k] 可以合并)
a[i].end<a[j].start(a[i] 和 a[j] 不能合并)
a[j].end<a[k].start(a[j] 和 a[k] 不能合并)
a[i].end≥a[k].start(a[i] 和 a[k] 可以合并)
我们联立这些不等式,可以得到:
a[i].end<a[j].start≤a[j].end<a[k].start
产生了矛盾!这说明假设是不成立的。因此,所有能够合并的区间都必然是连续的。
我的思路
1.先判断该 intervals是否为空,为空则返回一个空的二维数组int[0][2]
2.不为空的话,先用Array.sort(T[] a,Comparator<? super T> c)来定制一个只比较数组的最左端并使用升序排序的Compare排序器
3.之后将二维数组封装在一个List集合里面,进行下一步比较
4.有两种情况
4.1. 如果第一个区间的最右端的值小于下一个区间的最左端的值,则在List集合中再添加一个区间
4.2. 如果第一个区间的最右端的值大于等于下一个区间最左端的值,则将第一个区间最右端的值修改为下一个区间最右端的值
5.将List转换为数组并以二维数组的形式返回即可
使用方法Arrays.sort和Comprator
Arrays.sort使用文档
- public static <T> void sort(T[] a, Comparator<? super T> c)
- 根据指定比较器引发的顺序对指定的对象数组进行排序。 数组中的所有元素都必须是指定比较相互比较的 (即,
c.compare(e1, e2)不得抛出ClassCastException任何元件e1和e2阵列中)。这种保证是稳定的 :相同的元素不会因排序而重新排序。
实现注意事项:此实现是一个稳定的,自适应的迭代合并输出,当输入数组部分排序时,需要远远少于n lg(n)的比较,同时在输入数组随机排序时提供传统mergesort的性能。 如果输入数组几乎排序,则实现需要大约n次比较。 临时存储要求从几乎排序的输入数组的小常量到随机排序的输入数组的n / 2个对象引用不等。
该实现在其输入数组中具有升序和降序的相同优势,并且可以利用同一输入数组的不同部分中的升序和降序。 它非常适合合并两个或多个排序数组:只需连接数组并对结果数组进行排序。
参数类型
T- 要排序的对象的类参数
a- 要排序的数组
c- 用于确定阵列顺序的比较器。null值表示应使用元素' natural ordering 。异常
ClassCastException- 如果数组包含使用指定比较器无法 相互比较的元素
IllegalArgumentException- (可选)如果发现比较器违反了Comparator合同
Comprator使用文档
Collections.sort或Arrays.sort),以便精确控制排序顺序。 比较器还可用于控制某些数据结构的顺序(例如sorted sets或sorted maps),或者为没有natural ordering的对象集合提供排序。比较器
c对一组元素S施加的排序被认为与等号一致,当且仅当c.compare(e1, e2)==0具有与e1.equals(e2)(e1和e2在S中的S相同的布尔值时。当使用能够强加与equals不一致的排序的比较器来排序有序集(或有序映射)时,应该谨慎行事。 假设具有显式比较器
c的有序集(或有序映射)与从集合S提取的元素(或键)S。 如果c对S的排序与equals不一致,则排序集(或有序映射)将表现得“奇怪”。 特别是有序集(或有序映射)将违反集合(或映射)的一般合同,其定义为equals。例如,假设有两个元素
a和b,使(a.equals(b) && c.compare(a, b) != 0)为空TreeSet,比较器为c。 第二个add操作将返回true(并且树集的大小将增加)因为a和b在树集的视角中不相等,即使这与Set.add方法的规范相反。注意:这通常是一个好主意比较,也能实现
java.io.Serializable,因为它们可能被用来作为排序的序列化数据结构的方法(如TreeSet,TreeMap)。 为了使数据结构成功序列化,比较器(如果提供)必须实现Serializable。对于数学上的倾斜,即限定了施加顺序给定的比较器的关系
c上一组给定对象强加S是:{(x, y) such that c.compare(x, y) <= 0}.此总订单的商是:{(x, y) such that c.compare(x, y) == 0}.它从合同紧跟compare,该商数是一个等价关系S,并且实行排序是全序S。 当我们说c对S施加的排序与equals一致时 ,我们的意思是排序的商是由对象'equals(Object)方法定义的等价关系:{(x, y) such that x.equals(y)}.与
Comparable不同,比较器可以选择允许比较空参数,同时保持对等关系的要求。
声明
部分算法思路摘自力扣(位置在算法思路这个目录里),其余均为个人创作
作者:力扣官方题解
链接:https://leetcode.cn/problems/merge-intervals/
来源:力扣(LeetCode)