【机器学习 | ARIMA】经典时间序列模型ARIMA定阶最佳实践，确定不来看看？

在这里插入图片描述

🤵‍♂️ 个人主页: @AI_magician
📡主页地址：作者简介：CSDN内容合伙人，全栈领域优质创作者。
👨‍💻景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！🐱‍🏍
🙋‍♂️声明：本人目前大学就读于大二，研究兴趣方向人工智能&硬件（虽然硬件还没开始玩，但一直很感兴趣！希望大佬带带）

在这里插入图片描述

【深度学习 | 核心概念】那些深度学习路上必经的核心概念，确定不来看看？（一）作者：计算机魔术师版本： 1.0 （ 2023.8.27 ）

摘要：本系列旨在普及那些深度学习路上必经的核心概念，文章内容都是博主用心学习收集所写，欢迎大家三联支持！本系列会一直更新，核心概念系列会一直更新！欢迎大家订阅

该文章收录专栏
[✨— 《深入解析机器学习：从原理到应用的全面指南》 —✨]

@toc

ARIMA定阶解决方案

名称	介绍	优缺点
自相关函数（ACF）和偏自相关函数（PACF）	通过观察ACF和PACF图像的截尾性和拖尾性来确定AR和MA的阶数。	优点：简单直观，易于理解和实现。缺点：对于复杂的时间序列，图像解释可能不明确；需要主观判断截尾和拖尾的位置。
信息准则（AIC、BIC）	使用AIC（Akaike Information Criterion）或BIC（Bayesian Information Criterion）来选择最佳模型阶数。	优点：基于统计学原理，可自动选择模型阶数。缺点：对于大规模数据集，计算开销较大。
网格搜索	遍历多个ARIMA模型的参数组合，通过交叉验证或验证集性能来选择最佳模型。	优点：能够找到最佳参数组合。缺点：计算开销较大，需要尝试多个参数组合；可能受限于搜索范围和计算资源。
自动ARIMA（auto.arima）	自动选择ARIMA模型的阶数，基于AIC准则进行模型搜索和选择。	优点：自动化流程，省去手动选择模型阶数的步骤。缺点：对于复杂的时间序列，可能无法找到最佳模型。

ACF & PACF 定阶

使用**自相关函数（ACF）和偏自相关函数（PACF）**来确定AR和MA的阶数。ACF表示观察值与滞后版本之间的相关性，PACF表示观察值与滞后版本之间的直接相关性。

下面是ACF（自相关函数）和PACF（偏自相关函数）的绘图函数及其说明，以及对应的模板代码。

名称	说明	模板代码
`plot_acf`	绘制自相关函数（ACF）图	`plot_acf(x, lags=None, alpha=0.05, use_vlines=True, title='Autocorrelation', zero=False, vlines_kwargs=None, ax=None)`
`plot_pacf`	绘制偏自相关函数（PACF）图	`plot_pacf(x, lags=None, alpha=0.05, method='ywunbiased', use_vlines=True, title='Partial Autocorrelation', zero=False, vlines_kwargs=None, ax=None)`

函数参数说明：

x：要计算自相关或偏自相关的序列数据。
lags：要绘制的滞后阶数。默认为None，表示绘制所有滞后阶数。
alpha：置信区间的置信水平。默认为0.05，表示95%的置信水平。
use_vlines：是否在图中使用垂直线表示置信区间。默认为True。
title：图的标题。默认为"Autocorrelation"（自相关）或"Partial Autocorrelation"（偏自相关）。
zero：是否在图中包含零滞后（lag）线。默认为False。
vlines_kwargs：用于控制垂直线属性的可选参数。
ax：用于绘制图形的matplotlib轴对象。默认为None，表示创建一个新的轴对象。

示例代码：

对于经典的时间序列数据，您可以使用其他专门的库来获取，例如 pandas-datareader、yfinance、Alpha Vantage 等。

import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import pandas as pd
from statsmodels.datasets import get_rdataset
from statsmodels.tsa.arima.model import ARIMA

# 获取AirPassengers数据集
#data = get_rdataset('AirPassengers').data # Not do stationate

# 示例数据
data = [0, 1, 2, 3, 4, 5,6,7,8,9,10,11,12,13]

# 定义绘制自相关图&偏相关函数
def draw_acf_pcf(ts):
    sample_size = len(ts)
    max_lags = sample_size // 2 - 1  # 设置最大滞后期数为样本大小的50%
    plt.figure(facecolor='white', figsize=(10, 8))
    plot_acf(ts)
    plot_pacf(ts,lags = max_lags)
    plt.title('自相关图')
    plt.show()

当计算部分相关系数时，通常需要注意设置滞后期数（nlags）的值，以确保其不超过样本大小的50%。这是因为计算部分相关系数需要估计协方差矩阵的逆矩阵，而当滞后期数过大时，逆矩阵的计算可能会变得不稳定。这里默认为50% - 1

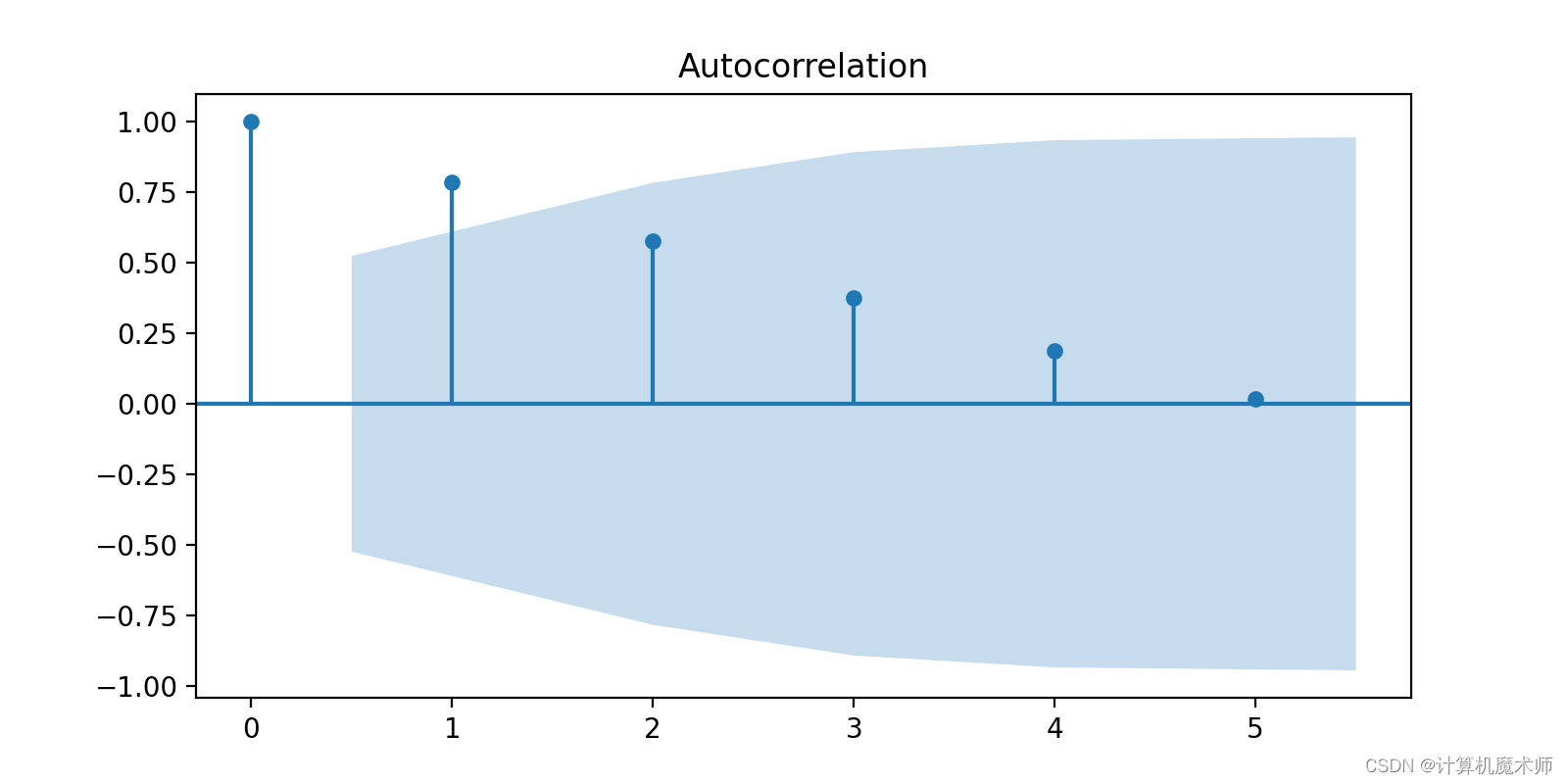
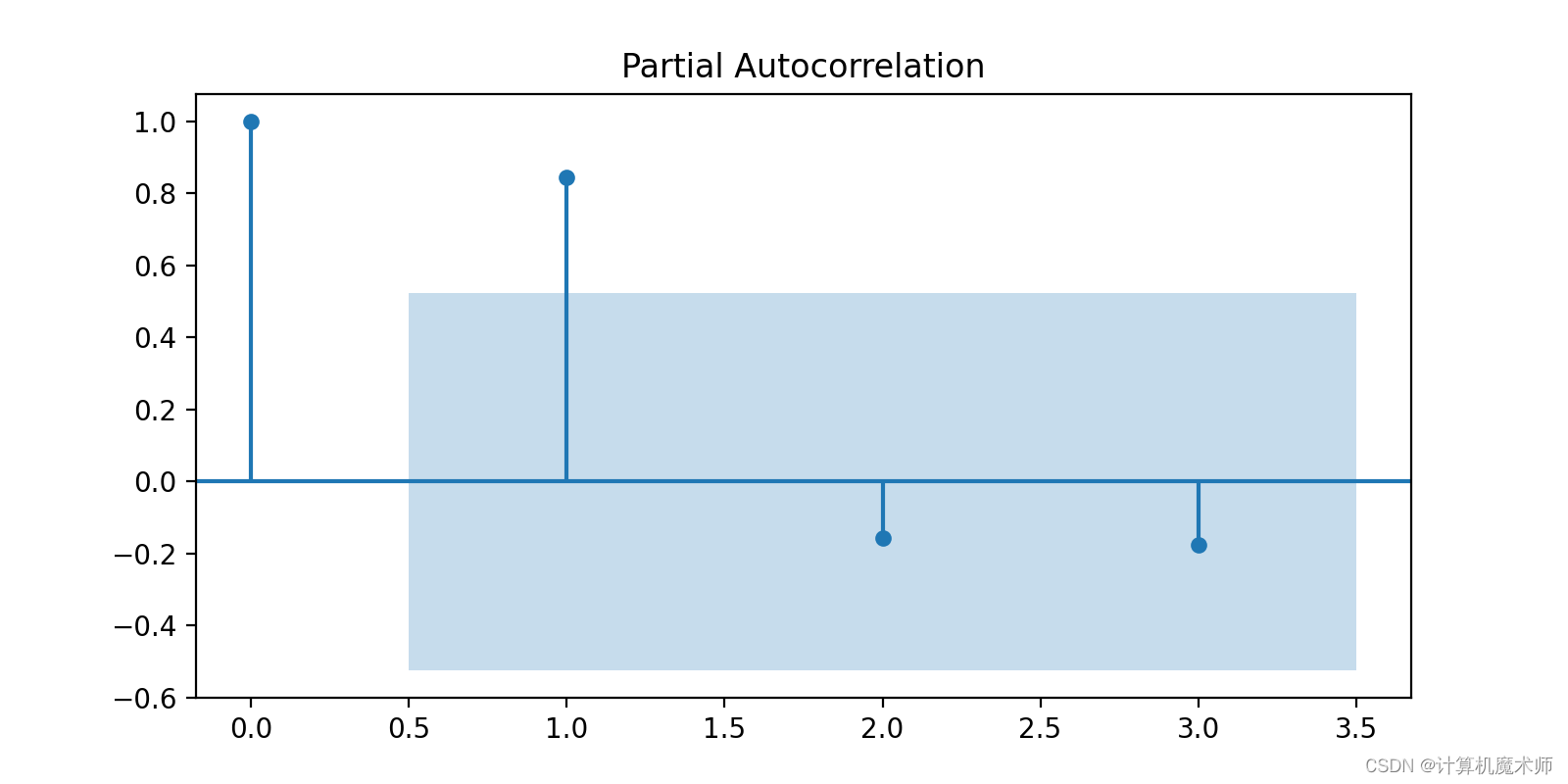
在这里插入图片描述

观察ACF图和PACF图的截尾性：首先，观察ACF图和PACF图的截尾性。在ACF图中，如果自相关系数在滞后阶数后逐渐衰减并趋于零，这表明可以考虑使用自回归（AR）模型（拖尾）。在PACF图中，如果偏相关系数在滞后阶数后截尾并趋于零，这表明可以考虑使用滑动平均（MA）模型。（截尾）
观察ACF图和PACF图的截尾性：首先，观察ACF图和PACF图的截尾性。在ACF图中，如果自相关系数在滞后阶数后逐渐衰减并趋于零，这表明可以考虑使用自回归（AR）模型。在PACF图中，如果偏相关系数在滞后阶数后截尾并趋于零，这表明可以考虑使用滑动平均（MA）模型。
确定AR模型阶数：根据ACF图的截尾性，确定AR模型的阶数。阶数可以根据ACF图中第一个超过置信区间的滞后阶数来确定。
确定MA模型阶数：根据PACF图的截尾性，确定MA模型的阶数。阶数可以根据PACF图中第一个超过置信区间的滞后阶数来确定。
确定ARMA模型阶数：如果ACF图和PACF图都有截尾性，可以考虑使用ARMA模型。阶数可以根据ACF图和PACF图的信息共同确定。
确定AR模型阶数：根据ACF图的截尾性，确定AR模型的阶数。阶数可以根据ACF图中第一个超过置信区间的滞后阶数来确定。
确定MA模型阶数：根据PACF图的截尾性，确定MA模型的阶数。阶数可以根据PACF图中第一个超过置信区间的滞后阶数来确定。
确定ARMA模型阶数：如果ACF图和PACF图都有截尾性，可以考虑使用ARMA模型。阶数可以根据ACF图和PACF图的信息共同确定。

可以看到自相关图出现拖尾，而偏向关图在2阶截尾，所以选用ARIMA(2, K , 1)

信息准则（AIC、BIC）定阶

信息准则（Information Criteria）是一种用于模型选择和定阶（model selection and model order determination）的统计方法。其中两个常用的信息准则是AIC（Akaike Information Criterion）和BIC（Bayesian Information Criterion）。它们的目标是在考虑模型拟合优度的同时，惩罚模型复杂度，避免过度拟合。

AIC和BIC的原理都基于信息理论。信息理论是研究信息传输、压缩和表示的数学理论，其中一个重要概念是信息熵（Information Entropy）。信息熵度量了一个随机变量的不确定性或信息量。

AIC的计算公式为：AIC = 2k - 2ln(L)，其中k是模型参数的数量，L是似然函数的最大值。AIC的原理是通过最大化似然函数来拟合数据，然后用模型参数的数量k对拟合优度进行惩罚。AIC的数值越小，表示模型的拟合优度越好。

BIC的计算公式为：BIC = k * ln(n) - 2ln(L)，其中k是模型参数的数量，n是样本量，L是似然函数的最大值。BIC的原理是在AIC的基础上引入了对样本量n的惩罚。BIC的数值越小，表示模型的拟合优度越好。

下面通过一个简单的案例来说明AIC和BIC的应用：

假设有一个简单的线性回归模型，要根据数据集选择模型的阶数（即变量的数量）。

假设我们有以下数据集：

X = [1, 2, 3, 4, 5]
Y = [2, 4, 6, 8, 10]

我们可以考虑的模型阶数有1、2、3、4。对于每个阶数，我们拟合相应的线性回归模型，并计算AIC和BIC的值。

阶数为1时，模型为 Y = β0 + β1X
阶数为2时，模型为 Y = β0 + β1X + β2X^2
阶数为3时，模型为 Y = β0 + β1X + β2X^2 + β3X^3
阶数为4时，模型为 Y = β0 + β1X + β2X^2 + β3X^3 + β4X^4

对于每个模型，我们可以计算出似然函数的最大值（最小二乘法），然后带入AIC和BIC的计算公式得到相应的值。假设计算结果如下：

阶数1的AIC = 10.2，BIC = 12.4
阶数2的AIC = 8.5，BIC = 12.0
阶数3的AIC = 7.8，BIC = 12.8
阶数4的AIC = 9.1，BIC = 15.6

根据AIC和BIC的值，我们可以选择AIC和BIC值最小的模型作为最优模型。在这个案例中，阶数为3的模型具有最小的AIC和BIC值，因此我们选择阶数为3的模型作为最优模型。

这个案例说明了AIC和BIC在模型选择和定阶中的应用过程。它们通过考虑模型的拟合优度和复杂度，帮助我们选择最优的模型，避免过度拟合。

以下是使用库的的实现，

# 通过BIC矩阵进行模型定阶
data_w = data_w.astype(float) 
pmax = 3 # 可以根据图选定
qmax = 3
bic_matrix = []  # 初始化BIC矩阵
for p in range(pmax+1):
    tmp = []
    for q in range(qmax+1):
        try:
            tmp.append(ARIMA(data_w, (p, 2, q)).fit().bic)   
        except:
            tmp.append(None)
        bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)
# 找出最小值位置
p, q = bic_matrix.stack().idxmin()
print('当BIC最小时，p值和q值分别为: ', p, q)

以下是具体代码实现，查看细节可以更好了解原理

import numpy as np
from sklearn.linear_model import LinearRegression
from scipy.stats import norm

def calculate_aic(n, k, rss):
    aic = 2 * k - 2 * np.log(rss)
    return aic

def calculate_bic(n, k, rss):
    bic = k * np.log(n) - 2 * np.log(rss)
    return bic

# 生成示例数据
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
Y = np.array([2, 4, 6, 8, 10])

# 计算模型的AIC和BIC值
n = len(X)  # 样本量
aic_values = []
bic_values = []

for k in range(1, 5):  # 尝试不同的阶数
    model = LinearRegression()
    model.fit(X[:, :k], Y)
    y_pred = model.predict(X[:, :k])
    rss = np.sum((Y - y_pred) ** 2)  # 残差平方和

    aic = calculate_aic(n, k, rss)
    bic = calculate_bic(n, k, rss)
    
    aic_values.append(aic)
    bic_values.append(bic)

# 选择最优模型的阶数
best_aic_index = np.argmin(aic_values)
best_bic_index = np.argmin(bic_values)

best_aic_order = best_aic_index + 1
best_bic_order = best_bic_index + 1

print("AIC values:", aic_values)
print("BIC values:", bic_values)
print("Best AIC order:", best_aic_order)
print("Best BIC order:", best_bic_order)

其实就是在机器学习的根据参数和残差作为损失值，选择损失值最小的

在这里插入图片描述

						  🤞到这里，如果还有什么疑问🤞
					🎩欢迎私信博主问题哦，博主会尽自己能力为你解答疑惑的！🎩
					 	 🥳如果对你有帮助，你的赞是对博主最大的支持！！🥳