旅行商问题（枚举，回溯，动态规划，贪心，分支界限）

文章目录

问题描述
暴力枚举
回溯法
动态规划法
贪心法
分支界限法

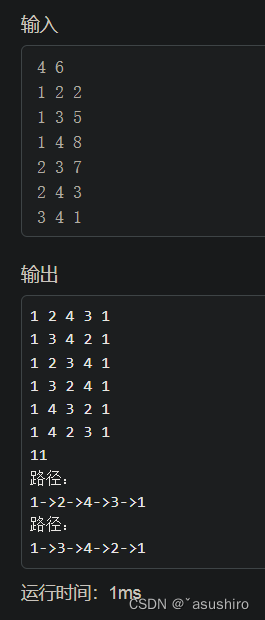
问题描述

假设有一个货郎担要拜访n个城市，他必须选择所要走的路程，路程的限制时每个城市只能拜访一次，而且最后要走到原来出发的城市，要求路径长度。

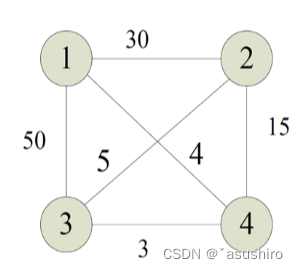
在这里插入图片描述

旅行商问题将要走过的城市建立成一个完全图。稠密图，所以用临接矩阵来存。
由于路径的特殊性，可以正走也可以反着走，所以一般存在两条最优路径同时也可以用这条性质检验算法的正确性。

暴力枚举

使用dfs枚举每一个点，不适用剪枝的话就是暴力枚举方法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10;

int g[N][N], n, m;
int cv = 0, bv = 0x3f3f3f3f;
bool st[N];

vector<int> ans, x;

void dfs(int k)
{
    
    if (k == n)
    {
        // printf("before cv : %d\n", cv);
        // printf("last : {%d, %d} = %d\n", 1, x[k - 1], g[1][x[k - 1]]);
        cv += g[1][x[k - 1]];
        x.push_back(x[0]);
        
        for (auto i : x)
            printf("%d ", i);
        puts("");
        printf("{cv : %d}\n", cv);
        
        if(cv < bv)
        {
            
            bv = cv;
            ans = x;
        }
        cv -= g[1][x[k - 1]];//注意最后一个加的cv要减掉
        x.pop_back();//同样也要删掉
        return;
    }
    
    for (int i = 1; i <= n; i ++)
    {
        if (!st[i])
        {
            st[i] = true;
            x.push_back(i);//注意x的添加要在前面不然后面下标会出错
            cv += g[x[k - 1]][i];
            // printf("{%d, %d} : %d\n", x[k - 1], i,  g[x[k - 1]][i]);
            dfs(k + 1);
            cv -= g[x[k - 1]][i];
            x.pop_back();
            st[i] = false;
        }
    }
}

void out()
{
    puts("路径为：");
    for (int i = 0; i <= n; i ++){
        printf("%d", ans[i]);
        printf(i == n ? "\n" : "->");
    }
}

int main()
{
    memset(g, 0x3f, sizeof g);
    
    scanf("%d%d", &n, &m);
    
    for (int i = 0; i < m; i ++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    for (int i = 0; i <= n; i ++) g[i][i] = 0; 
    
    st[1] = true; 
    x.push_back(1);
    dfs (1);
    puts("最短路径为：");
    printf("%d\n", bv);
    out();

    reverse(ans.begin(), ans.end());
    out();
    puts("");
    
    return 0;
}

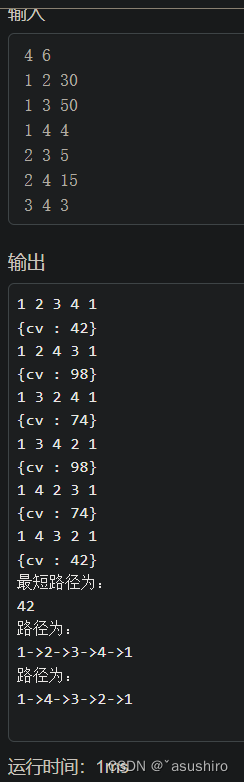
在这里插入图片描述

回溯法

回溯法就是在暴力枚举的是后加上剪枝函数减少枚举的结点数目
剪枝函数为
左剪枝：
$当 c v > b v 时减去$
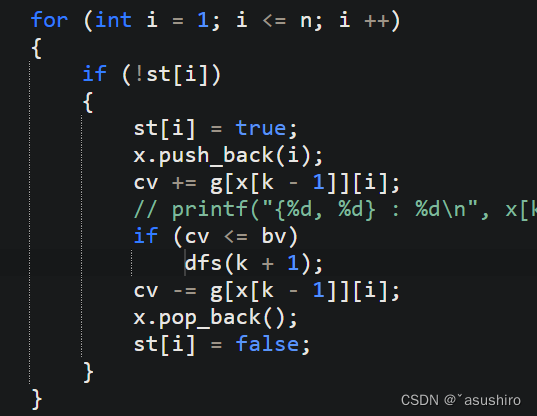
在这里插入图片描述
在暴力枚举的基础上加上这个剪枝函数就行

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10;

int g[N][N], n, m;
int cv = 0, bv = 0x3f3f3f3f;
bool st[N];

vector<int> ans, x;

void dfs(int k)
{
    
    if (k == n)
    {
        // printf("before cv : %d\n", cv);
        // printf("last : {%d, %d} = %d\n", 1, x[k - 1], g[1][x[k - 1]]);
        cv += g[1][x[k - 1]];
        x.push_back(x[0]);
        
        for (auto i : x)
            printf("%d ", i);
        puts("");
        printf("{cv : %d}\n", cv);
        
        if(cv < bv)
        {
            
            bv = cv;
            ans = x;
        }
        cv -= g[1][x[k - 1]];//注意最后一个加的cv要减掉
        x.pop_back();//同样也要删掉
        return;
    }
    
    for (int i = 1; i <= n; i ++)
    {
        if (!st[i])
        {
            st[i] = true;
            x.push_back(i);
            cv += g[x[k - 1]][i];
            // printf("{%d, %d} : %d\n", x[k - 1], i,  g[x[k - 1]][i]);
            if (cv <= bv)
                dfs(k + 1);
            cv -= g[x[k - 1]][i];
            x.pop_back();
            st[i] = false;
        }
    }
}

void out()
{
    puts("路径为：");
    for (int i = 0; i <= n; i ++){
        printf("%d", ans[i]);
        printf(i == n ? "\n" : "->");
    }
}

int main()
{
    memset(g, 0x3f, sizeof g);
    
    scanf("%d%d", &n, &m);
    
    for (int i = 0; i < m; i ++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    for (int i = 0; i <= n; i ++) g[i][i] = 0; 
    
    st[1] = true; 
    x.push_back(1);
    dfs (1);
    puts("最短路径为：");
    printf("%d\n", bv);
    out();

    reverse(ans.begin(), ans.end());
    out();
    puts("");
    
    return 0;
}

搜索的结点数变成了
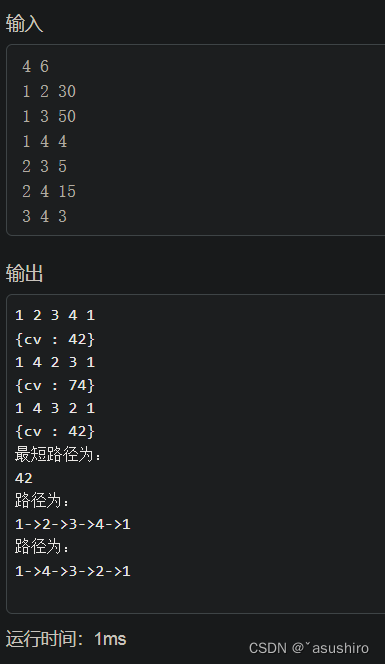
在这里插入图片描述
相比穷举减少了搜索的结点数

动态规划法

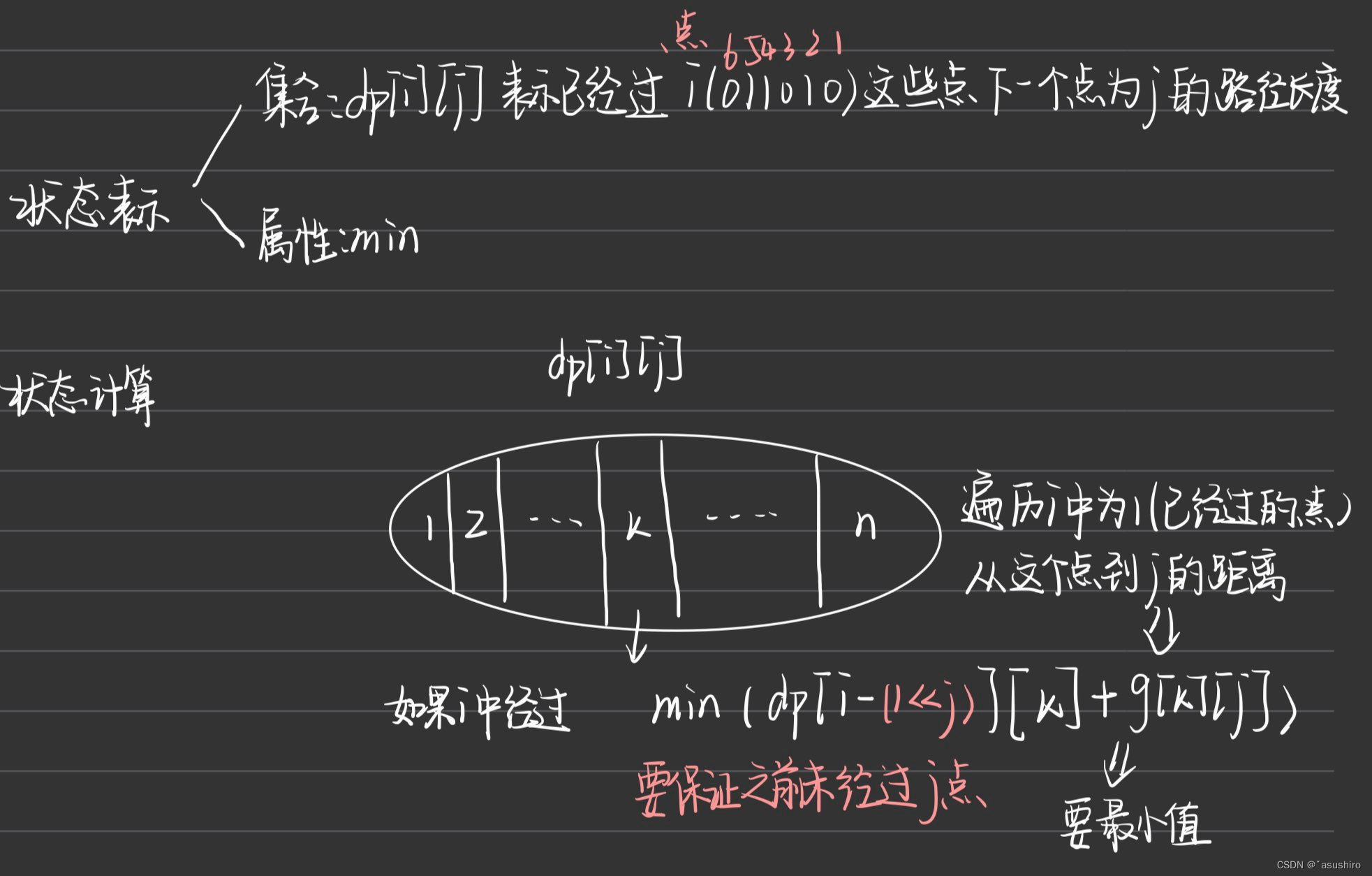
状态压缩dp
利用一个int位中的32位0/1bit码来表示图走了哪些点，如果此位为1表示经过，0表示还未经过

类似题目AcWing 91. 最短Hamilton路径

在这里插入图片描述

/*
    由于要遍历每一个点所以不能用最短路径算法
    从一个已知点到另一个点只需要关注两个状态：1、终点是什么， 2、经过了哪些点
    而dp[i][j] 表示从0到终点j，经过了二进制状态（每个点有走过和没走两个状态）的点的路径
    状态计算：dp[i][j] <- dp[i - j][k](在已经经过的点中，去掉点j的方案取最小)
*/
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 21, M = 1 << N;
int dp[M][N];
int w[N][N];
int n;

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n; j ++)
            scanf("%d", &w[i][j]);
            
    memset(dp, 0x3f, sizeof dp);
    dp[1][0] = 0;
    
    for (int i = 0; i < 1 << n; i ++)
        for (int j = 0; j < n; j ++)
            if (i >> j & 1)
                for (int k = 0; k < n; k ++ )
                    if (i >> k & 1)
                        dp[i][j] = min(dp[i][j], dp[i - (1 << j)][k] + w[j][k]);// 转移到达第i个点时将第i个点的状态要去掉就
                        // 例如要将100101的第2个点去掉就需要 - 000100 = 100001
                        
    printf("%d\n", dp[(1 << n) - 1][n - 1]);// 100000 - 000001 = 0111111 要将n - 1位全置位为1只需要用n为1后面为0减个位1即可
    return 0;
}

贪心法

贪心就是从起点开始每次走从这个点出发权重最小的边
但是这个寻找局部最优解的过程找到的并不是全局最优解
思路和生成最小生成树的思路一样，由于是完全图稠密图，所以使用prim算法更好

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int g[N][N], dist[N];
bool st[N];
int n, m;
vector<int> ans;

int prime()
{
    memset(dist, 0x3f, sizeof dist);
    int res = 0;// 最小生成树中的权重之和

    for (int i = 0; i < n; i ++)
    {
        int t = -1;// t表示集合外与集合相连的边最小的结点
        for (int j = 1; j <= n; j ++)
            if (!st[j] && (t == -1 || dist[j] < dist[t]))// 集合外的，第一次直接赋值，值更小的
                t = j;

        st[t] = true;// 加入集合
        ans.push_back(t);
        
        if (i && dist[t] == INF) return INF;// 不是第一个节点且到集合的距离无穷，说明各个结点都不连通
        if (i) res += dist[t];

        for (int j = 1; j <= n; j ++)
            dist[j] = min (dist[j], g[t][j]);// 更新与集合相连的最小值
    }

    return res;
}

void out()
{
    puts("路径：");
    for (int i = 0; i <= n; i ++)
    {
        printf("%d", ans[i]);
        printf(i == n ? "\n" : "->");
    }
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);

    for (int i = 0; i < m; i ++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min (g[a][b], c);// 无向图要将两个方向的边都赋上权重
    }
    
    int res = prime();
    if (res == INF) puts("impossible");
    else printf("%d\n", res + g[ans[n - 1]][1]);
    
    ans.push_back(ans[0]);
    
    out();
    reverse(ans.begin(), ans.end());
    out();
    
    return 0;
}

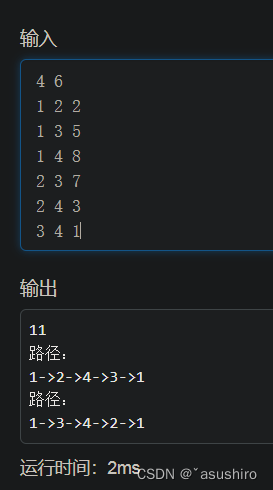
在这里插入图片描述

分支界限法

使用优先队列形式
cc为当前代价，rc为剩余结点的最小出边代价和
下界函数为: cc + rc
左剪枝：
$当 cc > b c 时剪枝$
右剪枝：
$当 cc + rc > b c 是剪枝$

归结左右剪枝都可以用bound = cc + rc进行剪枝

剩余结点最小出边代价和就是枚举剩余每条结点对没给结点只算最小的出边

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>

using namespace std;

const int N = 16;
const int INF = 0x3f3f3f3f;

int g[N][N], n, m, bc = INF;
vector<int> ans;

struct Node {
    int idx, cost, bound;
    vector<int> path;
    bool st[N];

    bool operator<(const Node& other) const {
        return bound + cost > other.bound + other.cost;  // 按照 bound + cost 降序排序
    }
};

int bound(const Node& x) {
    int minCost = 0;
    for (int i = 1; i <= n; ++i) {
        if (x.st[i]) {
            int m = INF;
            for (int j = 1; j <= n; ++j) {
                if (x.st[j]) {
                    m = min(m, g[i][j]);
                }
            }
            minCost += m;
        }
    }
    return minCost;
}

void bfs() {
    priority_queue<Node> heap;

    Node head = {1, 0, 0, {1}, {false}};
    head.st[1] = true;

    heap.push(head);

    while (heap.size()) {
        auto t = heap.top();
        heap.pop();

        if (t.idx == n) {
            int cc = t.cost + g[t.path[t.idx - 1]][1];
            for (auto i : t.path)
                printf("%d ", i);
            printf("%d", 1);
            puts("");
            if (cc < bc)
            {
                bc = cc;
                ans = t.path;
            }
            continue;
        }

        for (int i = 1; i <= n; ++i) {
            if (!t.st[i]) {
                Node newNode = t;
                newNode.st[i] = true;
                newNode.path.push_back(i);
                newNode.cost += g[newNode.path[newNode.idx - 1]][i];
                newNode.idx++;
                newNode.bound = bound(newNode); 
                if(newNode.bound < bc)//左右剪枝通用，因为是排列树左右都要算下界函数
                    heap.push(newNode);
            }
        }
    }
}

void out()
{
    puts("路径：");
    for (int i = 0; i <= n; i ++)
    {
        printf("%d", ans[i]);
        printf(i == n ? "\n" : "->");
    }
}

int main() {
    memset(g, 0x3f, sizeof g);

    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; ++i) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    bfs();
    printf("%d\n", bc);
    ans.push_back(ans[0]);
    
    out();
    reverse(ans.begin(), ans.end());
    out();
    return 0;
}

在这里插入图片描述