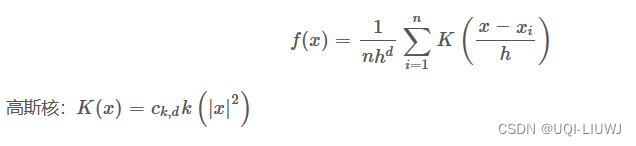1 算法介绍
- 一种基于质心的算法
- 通过更新候选质心使其成为给定区域内点的均值
- 候选质心的位置是通过一种称为“爬山”技术迭代调整的,该技术找到估计的概率密度的局部最大值
1.1 基本形式
- 给定d维空间的n个数据点集X,那么对于空间中的任意点x的均值漂移向量基本形式可以表示为:
- 其中Sk表示数据集的点到x的距离小于球半径h的数据点
- 漂移过程就类似于”梯度下降“
- 通过计算漂移向量,然后把球圆心x的位置更新一下
- 求解一个向量,使得圆心一直往数据集密度最大的方向移动(每次迭代找到圆里面的平均位置作为新的圆心位置)

1.2 加入核函数的漂移向量
- 引入核函数可以知道数据集的密度,梯度是函数增加最快的方向
- 这里的核函数为
- 对每个点的核函数求微分,有:

- g(x)=-k'(x)
- 第二个中括号前面的是实数值
- 第二项的向量方向与梯度方向一致
- 所以令加入核函数后的偏移向量为:

- 继续
1.3 聚类流程
假设在一个多维空间中有很多数据点需要进行聚类,Mean Shift的过程如下:
- 在未被标记的数据点中随机选择一个点作为中心center;
- 找出离center距离在bandwidth之内的所有点,记做集合M,认为这些点属于簇c
- 同时,把这些求内点属于这个类的频率加1,这个参数将用于最后步骤的分类
- 以center为中心点,计算从center开始到集合M中每个元素的向量,将这些向量相加,得到向量shift 【如果是带核函数的均值漂移,那么m(x)有额外的计算方式】
- center = center+shift。即center沿着shift的方向移动,移动距离是||shift||
- 重复步骤2、3、4,直到shift的大小很小(就是迭代到收敛),记住此时的center
- 这个迭代过程中遇到的点都应该归类到簇c
- 如果收敛时当前簇c的center与其它已经存在的簇c2中心的距离小于阈值,那么把c2和c合并。否则,把c作为新的聚类,增加1类
- 重复1、2、3、4、5直到所有的点都被标记访问。
- 分类:根据每个类,对每个点的访问频率,取访问频率最大的那个类,作为当前点集的所属类。
对新样本进行标记是通过找到给定样本的最近质心来执行的。
2 sklearn 实现
2.1 基本使用方法
class sklearn.cluster.MeanShift(
*,
bandwidth=None,
seeds=None,
bin_seeding=False,
min_bin_freq=1,
cluster_all=True,
n_jobs=None,
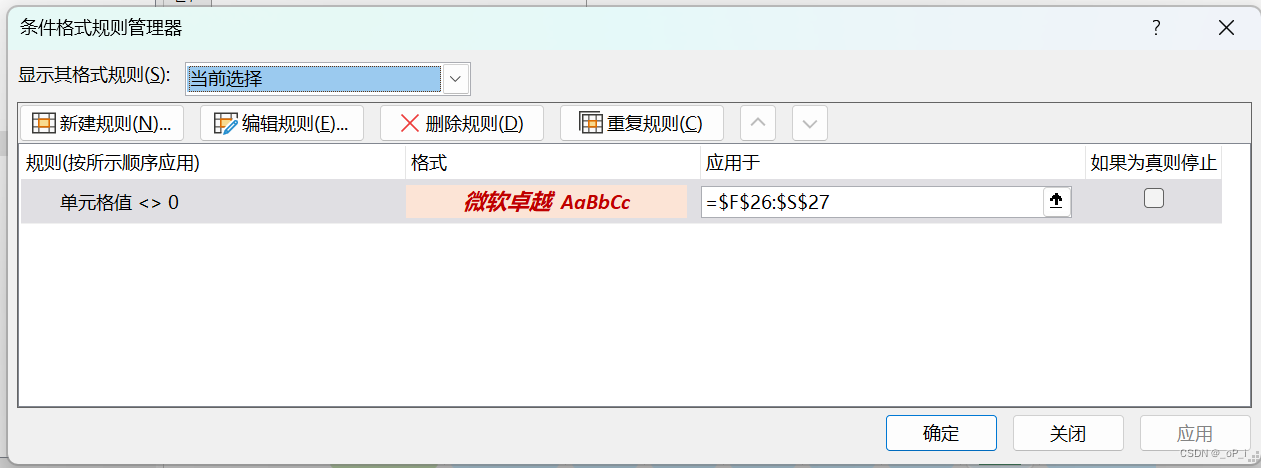
max_iter=300)2.2 主要参数
| bandwidth | 搜寻圆的大小 |
| seeds | 用于初始化核的种子 |
| cluster_all | 如果为true,则所有点都被聚类,即使是那些不在任何核内的孤儿点也一样。孤儿被分配到最近的核。 如果为false,则孤儿的聚类标签为-1 |
2.3 举例
from sklearn.cluster import MeanShift
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
ms=MeanShift(bandwidth=1).fit(X)
ms.cluster_centers_
'''
array([[10., 4.],
[10., 2.],
[10., 0.],
[ 1., 4.],
[ 1., 2.],
[ 1., 0.]])
'''
ms.labels_
#array([4, 3, 5, 1, 0, 2], dtype=int64)