Transformer
encoder-decoder架构
Encoder:将输入序列转换为一个连续向量空间中的表示。Encoder通常是一个循环神经网络(RNN)或者卷积神经网络(CNN),通过对输入序列中的每个元素进行编码,得到一个连续向量序列。
Decoder:将连续向量序列转换为输出序列。Decoder通常也是一个RNN或者CNN,它接收Encoder输出的向量序列作为输入,通过逐步生成一个输出序列。
基础模块
encoder:多头注意力机制+残差层+layer normalization
decoder:多了个带掩码的masked多头注意力机制,该masked多头注意力机制主要是让当前输入序列只得到当前时刻以前的信息,而没有后面的信息。
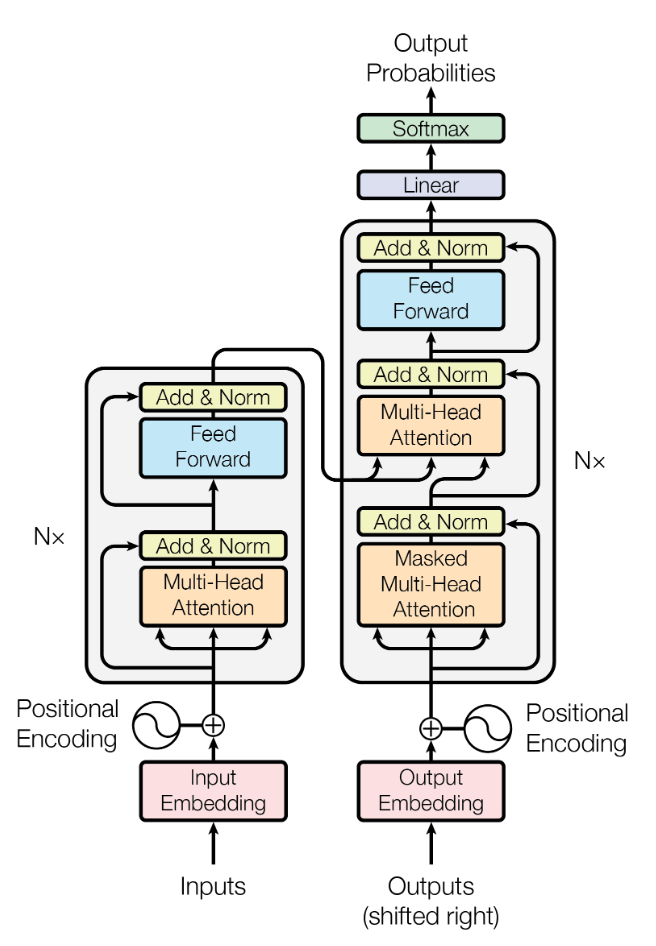
- 每一层的维度都设置为512,为了简化残差连接
Layer Normalization
为了适应序列不等长,其是针对每一个样本自己的特征进行normalization。
Layer Normalization(层归一化)是一种用于神经网络的归一化技术,用于缓解深层网络中的梯度消失和梯度爆炸问题。与 Batch Normalization(批归一化)相比,Layer Normalization 不依赖于批量的大小,因此更适合于在较小的批量上训练网络。
Layer Normalization 与 Batch Normalization 不同之处在于,Layer Normalization 是在每个样本的特征维度上进行归一化,而不是在批量维度上进行归一化。具体而言,设一个批量包含
m
m
m 个样本,每个样本的特征维度为
d
d
d,对于每个样本
x
∈
R
d
x \in \mathbb{R}^d
x∈Rd,Layer Normalization 将其转换为:
LayerNorm
(
x
)
=
γ
σ
(
x
−
μ
)
+
β
\text{LayerNorm}(x) = \frac{\gamma}{\sigma} (x - \mu) + \beta
LayerNorm(x)=σγ(x−μ)+β
其中
μ
\mu
μ 和
σ
\sigma
σ 分别是样本
x
x
x 在特征维度上的均值和标准差,即:
μ
=
1
d
∑
i
=
1
d
x
i
,
σ
=
1
d
∑
i
=
1
d
(
x
i
−
μ
)
2
\mu = \frac{1}{d} \sum_{i=1}^d x_i, \quad \sigma = \sqrt{\frac{1}{d} \sum_{i=1}^d (x_i - \mu)^2}
μ=d1i=1∑dxi,σ=d1i=1∑d(xi−μ)2
γ
\gamma
γ 和
β
\beta
β 分别是可学习的缩放因子和偏置项,这两个参数可以用梯度下降等优化算法来学习得到。
在神经网络中,Layer Normalization 可以用于每个神经层的输入,例如在多头自注意力机制中,可以对每个注意力头的输入进行归一化。Layer Normalization 能够有效地缓解深层网络中的梯度消失和梯度爆炸问题,并提高网络的泛化能力。
Position Embedding
因为Transformer没有采用RNN的结构,而是使用的全局信息,不能单词的顺序信息,所以通过对其使用Position Embedding进行编码,保持单词再序列中的相对或绝对位置。
P
E
(
p
o
s
,
2
i
)
=
sin
(
p
o
s
/
1000
0
2
i
/
d
)
P
E
(
p
o
s
,
2
i
+
1
)
=
cos
(
p
o
s
/
1000
0
2
i
/
d
)
\begin{array}{c} P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d}\right) \\ P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d}\right) \end{array}
PE(pos,2i)=sin(pos/100002i/d)PE(pos,2i+1)=cos(pos/100002i/d)
pos 表示单词在句子中的位置,d 表示 PE的维度 (与词 Embedding 一样),2i 表示偶数的维度,2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)。使用这种公式计算 PE 有以下的好处:
- 使 PE 能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有 20 个单词,突然来了一个长度为 21 的句子,则使用公式计算的方法可以计算出第 21 位的 Embedding。
- 可以让模型容易地计算出相对位置,对于固定长度的间距 k,PE(pos+k) 可以用 PE(pos) 计算得到。因为$ Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)$
将单词的词 Embedding 和位置 Embedding 相加,就可以得到单词的表示向量 x,x 就是 Transformer 的输入
- 以下是通过代码实现position embedding,需要对原式子进行解析操作的过程
令 a n g l e = p o s / 1000 0 2 i / d l n ( a n g l e ) = l n p o s − l n 1000 0 2 i / d = l n p o s + l n 1000 0 − 2 i / d = l n p o s − ( 2 i / d ) l n 10000 a n g l e = e x p ( l n p o s − ( 2 i / d ) l n 10000 ) = p o s ∗ 2 i ∗ ( − l n 10000 / d ) \begin{aligned} &令angle=pos/10000^{2i/d}\\ &ln(angle)=ln^{pos}-ln^{10000^{2i/d}}=ln^{pos}+ln^{10000^{-2i/d}}=ln^{pos}-(2i/d)ln^{10000}\\ &angle=exp(ln^{pos}-(2i/d)ln^{10000})=pos*2i*(-ln^{10000}/d) \end{aligned} 令angle=pos/100002i/dln(angle)=lnpos−ln100002i/d=lnpos+ln10000−2i/d=lnpos−(2i/d)ln10000angle=exp(lnpos−(2i/d)ln10000)=pos∗2i∗(−ln10000/d)
维度拓展
总的来说,就是在位置编码时添加一个batch层,用来与输入相加
在 Transformer 中,位置编码是通过将位置向量与输入词向量相加得到的。位置向量的维度是 d model d_{\text{model}} dmodel,即 Transformer 模型中词向量的维度。而输入的词向量的维度是$ (\text{sequence length}, d_{\text{model}})$,表示一个输入序列中每个词汇的词向量,而通常我们会将输入的向量维度变为:
x: [seq_len, batch_size, d_model]也就是在输入的时候加入了批量batch。
为了将位置向量与每个输入词向量相加,我们需要确保它们的维度是匹配的。但是位置向量只有一个维度,而输入词向量有两个维度,因此它们的维度并不匹配。因此,我们需要通过增加一个维度来匹配它们的维度。
具体来说,增加的维度是在最前面添加的,这样可以将位置向量的维度从 d model d_{\text{model}} dmodel 变为 1。这可以通过 PyTorch 中的
unsqueeze(0)操作来实现,它会在第 0 维上添加一个大小为 1 的维度,将位置向量的维度从 d model d_{\text{model}} dmodel变为 1。这样,位置向量的形状就变成了 ( 1 , d model ) (1, d_{\text{model}}) (1,dmodel),可以与输入词向量的形状 ( sequence length , d model ) (\text{sequence length}, d_{\text{model}}) (sequence length,dmodel) 进行广播相加。最后,为了保证位置向量和输入词向量的维度顺序一致,需要使用
transpose(0, 1)将位置向量的第 0 维和第 1 维交换,将位置向量的形状从$ (1, d_{\text{model}}) 变成 变成 变成(\text{sequence length}, 1, d_{\text{model}})$,这样就可以与输入词向量进行相加操作了。Dropout
此处的dropout层用来抛弃部分编码,以使得该模型适应在没有完整的位置编码后,对未知序列的编码能具有更好的可适性。
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
#unsqueeze是将dimension维度的中在第0维增加一个维度,而transpose则是将0,1维度进行交换
pe = pe.unsqueeze(0).transpose(0, 1)
self.register_buffer('pe', pe)
def forward(self, x):
"""
x: [seq_len, batch_size, d_model]
"""
x = x + self.pe[:x.size(0), :]
return self.dropout(x)
模型架构
Attention层
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
注意力函数可以描述为将查询和一组键值对映射到输出,其中query、key、val和输出都是向量。输出为val的加权和,其中分配给每个值的权重由query与相应键的兼容性函数(相似度)计算。
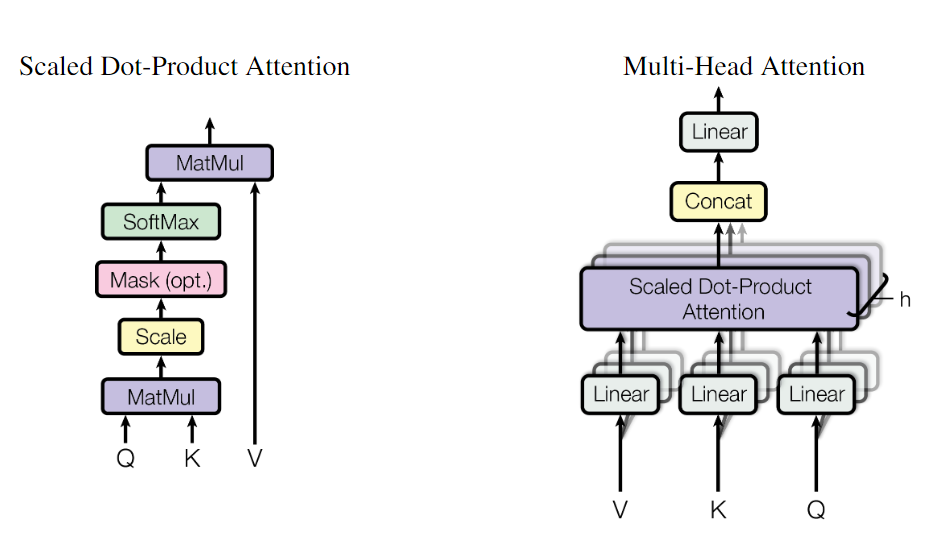 $$ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V $$ 对于较小的 $dk$ 值,这两种机制的表现相似,但加性注意力优于点积注意力,而不会缩放较大的 dk 值 。我们怀疑对于较大的$dk$值,点积的幅度较大,导致将softmax函数推入梯度极小的区域。为了抵消这种影响,我们将点积缩放$\frac{1}{\sqrt{d_k}}$,$d_k$为维度
$$ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V $$ 对于较小的 $dk$ 值,这两种机制的表现相似,但加性注意力优于点积注意力,而不会缩放较大的 dk 值 。我们怀疑对于较大的$dk$值,点积的幅度较大,导致将softmax函数推入梯度极小的区域。为了抵消这种影响,我们将点积缩放$\frac{1}{\sqrt{d_k}}$,$d_k$为维度
自注意力机制中存在的Mask则是用来将当前时刻之后的信息全置于0,以此让当前输出信息,只包含当前时刻以前的信息,用于decoder。
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super(ScaledDotProductAttention, self).__init__()
def forward(self, Q, K, V, attn_mask):
"""
Q: [batch_size, n_heads, len_q, d_k]
K: [batch_size, n_heads, len_k, d_k]
V: [batch_size, n_heads, len_v(=len_k), d_v]
attn_mask: [batch_size, n_heads, seq_len, seq_len]
说明:在encoder-decoder的Attention层中len_q(q1,..qt)和len_k(k1,...km)可能不同
"""
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k) # scores : [batch_size, n_heads, len_q, len_k]
# mask矩阵填充scores(用-1e9填充scores中与attn_mask中值为1位置相对应的元素)
scores.masked_fill_(attn_mask, -1e9) # Fills elements of self tensor with value where mask is True.
attn = nn.Softmax(dim=-1)(scores) # 对最后一个维度(v)做softmax
# scores : [batch_size, n_heads, len_q, len_k] * V: [batch_size, n_heads, len_v(=len_k), d_v]
context = torch.matmul(attn, V) # context: [batch_size, n_heads, len_q, d_v]
# context:[[z1,z2,...],[...]]向量, attn注意力稀疏矩阵(用于可视化的)
return context, attn
多头注意力机制
多头注意力机制将注意力机制在不同的子空间中独立地执行,以便于模型能够同时关注不同的语义信息。在多头注意力机制中,输入序列先经过一次线性变换,然后被划分为多个子序列,每个子序列被映射到一个不同的注意力子空间中。
- 不同子空间,多个,给注意力提供多种可能性,让不同的embedded能有多种关系的计算
具体来说,设输入序列为 x ∈ R n × d \mathbf{x}\in\mathbb{R}^{n\times d} x∈Rn×d,其中 n n n是序列长度, d d d是每个位置的向量表示维度。对输入序列进行线性变换,得到形状为 x ′ ∈ R n × d ′ \mathbf{x'}\in\mathbb{R}^{n\times d'} x′∈Rn×d′的中间表示,其中 d ′ d' d′是线性变换后的维度。然后,将 x ′ \mathbf{x'} x′沿第二个维度划分为 h h h个子序列 x ′ ( 1 ) , … , x ′ ( h ) \mathbf{x'}^{(1)},\dots,\mathbf{x'}^{(h)} x′(1),…,x′(h),每个子序列的形状为 x ′ ( i ) ∈ R n × d h \mathbf{x'}^{(i)}\in\mathbb{R}^{n\times d_h} x′(i)∈Rn×dh,其中 d h = d / h d_h=d/h dh=d/h。平均划分,也就是原论文中,当存在8个head时,每一个head的维度为 d k = d v = d model / h = 64 d_{k}=d_{v}=d_{\text {model }} / h=64 dk=dv=dmodel /h=64
在具体实现中,子向量的划分方式可以有所不同,有的实现采用可学习的划分方式,即引入一个形状为 ( d ′ , h ) (d',h) (d′,h)的权重矩阵 W ′ ∈ R d ′ × h \mathbf{W}'\in\mathbb{R}^{d'\times h} W′∈Rd′×h,将 x ′ \mathbf{x'} x′与 W ′ \mathbf{W}' W′进行矩阵乘法,得到形状为 ( n , h , d h ) (n,h,d_h) (n,h,dh)的输出,表示 h h h个子向量。无论采用哪种方式,多头注意力机制都能够对输入序列进行有效的建模和表达。
接下来,对于每个子序列 x ′ ( i ) \mathbf{x'}^{(i)} x′(i),计算其对应的注意力矩阵 A ( i ) ∈ R n × n \mathbf{A}^{(i)}\in\mathbb{R}^{n\times n} A(i)∈Rn×n,其中 A i j ( i ) \mathbf{A}_{ij}^{(i)} Aij(i)表示位置 i i i和位置 j j j之间的相似度,即它们在子空间 i i i中的注意力权重。注意力权重可以通过对 x ′ ( i ) \mathbf{x'}^{(i)} x′(i)进行一些简单的操作(如点积、加权平均等)来计算。然后,将每个子空间中的注意力权重 A ( i ) \mathbf{A}^{(i)} A(i)与对应的子序列 x ′ ( i ) \mathbf{x'}^{(i)} x′(i)进行加权求和,得到每个子空间的输出 y ( i ) ∈ R n × d h \mathbf{y}^{(i)}\in\mathbb{R}^{n\times d_h} y(i)∈Rn×dh,最后将 h h h个子空间的输出拼接在一起,得到形状为 y ∈ R n × d ′ \mathbf{y}\in\mathbb{R}^{n\times d'} y∈Rn×d′的最终输出。
通过将输入序列映射到
h
h
h个不同的距离空间中,多头注意力机制可以更好地捕捉不同级别的语义信息,并提高模型的泛化能力。
MultiHead
(
Q
,
K
,
V
)
=
Concat
(
head
1
,
…
,
head
h
)
W
O
where head
=
Attention
(
Q
W
i
Q
,
K
W
i
K
,
V
W
i
V
)
\begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_{1}, \ldots, \operatorname{head}_{\mathrm{h}}\right) W^{O} \\ \text { where head } & =\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}
MultiHead(Q,K,V) where head =Concat(head1,…,headh)WO=Attention(QWiQ,KWiK,VWiV)
代码实现
在多头注意力机制中,通过输入改变,可以同时实现Encoder、Decoder、Encoder-Decoder。
class MultiHeadAttention(nn.Module):
"""这个Attention类可以实现:
Encoder的Self-Attention
Decoder的Masked Self-Attention
Encoder-Decoder的Attention
输入:seq_len x d_model
输出:seq_len x d_model
"""
def __init__(self):
super(MultiHeadAttention, self).__init__()
self.W_Q = nn.Linear(d_model, d_k * n_heads, bias=False) # q,k必须维度相同,不然无法做点积
self.W_K = nn.Linear(d_model, d_k * n_heads, bias=False)
self.W_V = nn.Linear(d_model, d_v * n_heads, bias=False)
# 这个全连接层可以保证多头attention的输出仍然是seq_len x d_model
self.fc = nn.Linear(n_heads * d_v, d_model, bias=False)
def forward(self, input_Q, input_K, input_V, attn_mask):
"""
input_Q: [batch_size, len_q, d_model]
input_K: [batch_size, len_k, d_model]
input_V: [batch_size, len_v(=len_k), d_model]
attn_mask: [batch_size, seq_len, seq_len]
"""
residual, batch_size = input_Q, input_Q.size(0)
# 下面的多头的参数矩阵是放在一起做线性变换的,然后再拆成多个头,这是工程实现的技巧
# B: batch_size, S:seq_len, D: dim
# (B, S, D) -proj-> (B, S, D_new) -split-> (B, S, Head, W) -trans-> (B, Head, S, W)
# 线性变换 拆成多头
# Q: [batch_size, n_heads, len_q, d_k]
Q = self.W_Q(input_Q).view(batch_size, -1, n_heads, d_k).transpose(1, 2)
# K: [batch_size, n_heads, len_k, d_k] # K和V的长度一定相同,维度可以不同
K = self.W_K(input_K).view(batch_size, -1, n_heads, d_k).transpose(1, 2)
# V: [batch_size, n_heads, len_v(=len_k), d_v]
V = self.W_V(input_V).view(batch_size, -1, n_heads, d_v).transpose(1, 2)
# 因为是多头,所以mask矩阵要扩充成4维的
# attn_mask: [batch_size, seq_len, seq_len] -> [batch_size, n_heads, seq_len, seq_len]
attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)
# context: [batch_size, n_heads, len_q, d_v], attn: [batch_size, n_heads, len_q, len_k]
context, attn = ScaledDotProductAttention()(Q, K, V, attn_mask)
# 下面将不同头的输出向量拼接在一起
# context: [batch_size, n_heads, len_q, d_v] -> [batch_size, len_q, n_heads * d_v]
context = context.transpose(1, 2).reshape(batch_size, -1, n_heads * d_v)
# 这个全连接层可以保证多头attention的输出仍然是seq_len x d_model
output = self.fc(context) # [batch_size, len_q, d_model]
return nn.LayerNorm(d_model).to(device)(output + residual), attn
Feed Forward层
# Pytorch中的Linear只会对最后一维操作,所以正好是我们希望的每个位置用同一个全连接网络
class PoswiseFeedForwardNet(nn.Module):
def __init__(self):
super(PoswiseFeedForwardNet, self).__init__()
self.fc = nn.Sequential(
nn.Linear(d_model, d_ff, bias=False),
nn.ReLU(),
nn.Linear(d_ff, d_model, bias=False)
)
def forward(self, inputs):
"""
inputs: [batch_size, seq_len, d_model]
"""
residual = inputs
output = self.fc(inputs)
return nn.LayerNorm(d_model).to(device)(output + residual) # [batch_size, seq_len, d_model]
nn.LayerNorm(d_model).to(device)(output + residual) 等价于如下代码,其作用是将layernorm层应用于进行残差连接后的数据。
# 创建一个层归一化层并移动到指定设备上
layer_norm = nn.LayerNorm(d_model).to(device)
# 对输入张量进行残差连接并应用归一化层
normalized_output = layer_norm(output + residual)
Encoder
class EncoderLayer(nn.Module):
def __init__(self):
super(EncoderLayer, self).__init__()
self.enc_self_attn = MultiHeadAttention()#多头注意力机制
self.pos_ffn = PoswiseFeedForwardNet()#前向feedforward以及layer norm
def forward(self, enc_inputs, enc_self_attn_mask):
"""E
enc_inputs: [batch_size, src_len, d_model]
enc_self_attn_mask: [batch_size, src_len, src_len] mask矩阵(pad mask or sequence mask)
"""
# enc_outputs: [batch_size, src_len, d_model], attn: [batch_size, n_heads, src_len, src_len]
# 第一个enc_inputs * W_Q = Q
# 第二个enc_inputs * W_K = K
# 第三个enc_inputs * W_V = V
enc_outputs, attn = self.enc_self_attn(enc_inputs, enc_inputs, enc_inputs,
enc_self_attn_mask) # enc_inputs to same Q,K,V(未线性变换前)
enc_outputs = self.pos_ffn(enc_outputs)
# enc_outputs: [batch_size, src_len, d_model]
return enc_outputs, attn
多头注意力机制的输出是一个张量,其形状为 (batch_size, seq_length, d_model),其中 batch_size 表示输入数据的批量大小,seq_length 表示输入数据的序列长度,d_model 表示每个词汇的向量维度。在多头注意力机制中,对于每个头,会计算一组注意力权重,并将这些权重与对应的值向量相乘,得到每个头的输出向量。然后,将所有头的输出向量沿着最后一个维度进行拼接,得到最终的输出张量。
具体来说,在多头注意力机制中,输入先经过三个线性变换(即 W Q , W K , W V W_Q, W_K, W_V WQ,WK,WV)得到三个张量 Q , K , V Q, K, V Q,K,V。然后,将 Q , K Q, K Q,K 做点积,除以一个数 d k \sqrt{d_k} dk 进行缩放,并通过 softmax 函数计算每个词对所有词的注意力得分。得到每个头的注意力权重后,将其与对应的值向量 V V V 做加权和,得到每个头的输出向量。最后,将所有头的输出向量沿着最后一个维度进行拼接,得到多头注意力机制的最终输出张量。
因此,多头注意力机制的输出是一个维度为 (batch_size, seq_length, d_model) 的张量,其中每个位置包含着所有头的输出向量的拼接。可以将其作为后续网络的输入,例如 Transformer 中的前馈神经网络。
class Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
self.src_emb = nn.Embedding(src_vocab_size, d_model) # token Embedding
self.pos_emb = PositionalEncoding(d_model) # Transformer中位置编码时固定的,不需要学习
self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)])
def forward(self, enc_inputs):
"""
enc_inputs: [batch_size, src_len]
"""
enc_outputs = self.src_emb(enc_inputs) # [batch_size, src_len, d_model]
enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1) # [batch_size, src_len, d_model]
# Encoder输入序列的pad mask矩阵
enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs) # [batch_size, src_len, src_len]
enc_self_attns = [] # 在计算中不需要用到,它主要用来保存你接下来返回的attention的值(这个主要是为了你画热力图等,用来看各个词之间的关系
for layer in self.layers: # for循环访问nn.ModuleList对象
# 上一个block的输出enc_outputs作为当前block的输入
# enc_outputs: [batch_size, src_len, d_model], enc_self_attn: [batch_size, n_heads, src_len, src_len]
enc_outputs, enc_self_attn = layer(enc_outputs,
enc_self_attn_mask) # 传入的enc_outputs其实是input,传入mask矩阵是因为你要做self attention
enc_self_attns.append(enc_self_attn) # 这个只是为了可视化
return enc_outputs, enc_self_attns
Decoder
Masked机制
上面的pad mask是用来过滤输入时,输入的截止符end,可有可无。
第二个函数的subsequence是用来过滤输入时刻后的数据,当矩阵为1时,则将当前数据置 − ∞ - \infty −∞
def get_attn_pad_mask(seq_q, seq_k):
# pad mask的作用:在对value向量加权平均的时候,可以让pad对应的alpha_ij=0,这样注意力就不会考虑到pad向量
"""这里的q,k表示的是两个序列(跟注意力机制的q,k没有关系),例如encoder_inputs (x1,x2,..xm)和encoder_inputs (x1,x2..xm)
encoder和decoder都可能调用这个函数,所以seq_len视情况而定
seq_q: [batch_size, seq_len]
seq_k: [batch_size, seq_len]
seq_len could be src_len or it could be tgt_len
seq_len in seq_q and seq_len in seq_k maybe not equal
"""
batch_size, len_q = seq_q.size() # 这个seq_q只是用来expand维度的
batch_size, len_k = seq_k.size()
# eq(zero) is PAD token
# 例如:seq_k = [[1,2,3,4,0], [1,2,3,5,0]]
pad_attn_mask = seq_k.data.eq(0).unsqueeze(1) # [batch_size, 1, len_k], True is masked
return pad_attn_mask.expand(batch_size, len_q, len_k) # [batch_size, len_q, len_k] 构成一个立方体(batch_size个这样的矩阵)
def get_attn_subsequence_mask(seq):
"""建议打印出来看看是什么的输出(一目了然)
seq: [batch_size, tgt_len]
"""
attn_shape = [seq.size(0), seq.size(1), seq.size(1)]
# attn_shape: [batch_size, tgt_len, tgt_len]
subsequence_mask = np.triu(np.ones(attn_shape), k=1) # 生成一个上三角矩阵
subsequence_mask = torch.from_numpy(subsequence_mask).byte()
print(subsequence_mask)
return subsequence_mask # [batch_size, tgt_len, tgt_len]
# [[0, 1, 1, 1, 1, 1, 1],
# [0, 0, 1, 1, 1, 1, 1],
# [0, 0, 0, 1, 1, 1, 1],
# [0, 0, 0, 0, 1, 1, 1],
# [0, 0, 0, 0, 0, 1, 1],
# [0, 0, 0, 0, 0, 0, 1],
# [0, 0, 0, 0, 0, 0, 0]]], dtype=torch.uint8)
masked_fill(mask,value)方法有两个参数,mask和value,mask是一个pytorch张量(Tensor),元素是布尔值,value是要填充的值,填充规则是mask中取值为True位置对应于self的相应位置用value填充。
Decode layer
class DecoderLayer(nn.Module):
def __init__(self):
super(DecoderLayer, self).__init__()
self.dec_self_attn = MultiHeadAttention()
self.dec_enc_attn = MultiHeadAttention()
self.pos_ffn = PoswiseFeedForwardNet()
def forward(self, dec_inputs, enc_outputs, dec_self_attn_mask, dec_enc_attn_mask):
"""
dec_inputs: [batch_size, tgt_len, d_model]
enc_outputs: [batch_size, src_len, d_model]
dec_self_attn_mask: [batch_size, tgt_len, tgt_len]
dec_enc_attn_mask: [batch_size, tgt_len, src_len]
"""
# dec_outputs: [batch_size, tgt_len, d_model], dec_self_attn: [batch_size, n_heads, tgt_len, tgt_len]
dec_outputs, dec_self_attn = self.dec_self_attn(dec_inputs, dec_inputs, dec_inputs,
dec_self_attn_mask) # 这里的Q,K,V全是Decoder自己的输入
# dec_outputs: [batch_size, tgt_len, d_model], dec_enc_attn: [batch_size, h_heads, tgt_len, src_len]
dec_outputs, dec_enc_attn = self.dec_enc_attn(dec_outputs, enc_outputs, enc_outputs,
dec_enc_attn_mask) # Attention层的Q(来自decoder) 和 K,V(来自encoder)
dec_outputs = self.pos_ffn(dec_outputs) # [batch_size, tgt_len, d_model]
return dec_outputs, dec_self_attn, dec_enc_attn # dec_self_attn, dec_enc_attn这两个是为了可视化的
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
self.tgt_emb = nn.Embedding(tgt_vocab_size, d_model) # Decoder输入的embed词表
self.pos_emb = PositionalEncoding(d_model)
self.layers = nn.ModuleList([DecoderLayer() for _ in range(n_layers)]) # Decoder的blocks
def forward(self, dec_inputs, enc_inputs, enc_outputs):
"""
dec_inputs: [batch_size, tgt_len]
enc_inputs: [batch_size, src_len]
enc_outputs: [batch_size, src_len, d_model] # 用在Encoder-Decoder Attention层
"""
dec_outputs = self.tgt_emb(dec_inputs) # [batch_size, tgt_len, d_model]
dec_outputs = self.pos_emb(dec_outputs.transpose(0, 1)).transpose(0, 1).to(
device) # [batch_size, tgt_len, d_model]
# Decoder输入序列的pad mask矩阵(这个例子中decoder是没有加pad的,实际应用中都是有pad填充的)
dec_self_attn_pad_mask = get_attn_pad_mask(dec_inputs, dec_inputs).to(device) # [batch_size, tgt_len, tgt_len]
# Masked Self_Attention:当前时刻是看不到未来的信息的
dec_self_attn_subsequence_mask = get_attn_subsequence_mask(dec_inputs).to(
device) # [batch_size, tgt_len, tgt_len]
# Decoder中把两种mask矩阵相加(既屏蔽了pad的信息,也屏蔽了未来时刻的信息)
dec_self_attn_mask = torch.gt((dec_self_attn_pad_mask + dec_self_attn_subsequence_mask),
0).to(device) # [batch_size, tgt_len, tgt_len]; torch.gt比较两个矩阵的元素,大于则返回1,否则返回0
# 这个mask主要用于encoder-decoder attention层
# get_attn_pad_mask主要是enc_inputs的pad mask矩阵(因为enc是处理K,V的,求Attention时是用v1,v2,..vm去加权的,要把pad对应的v_i的相关系数设为0,这样注意力就不会关注pad向量)
# dec_inputs只是提供expand的size的
dec_enc_attn_mask = get_attn_pad_mask(dec_inputs, enc_inputs) # [batc_size, tgt_len, src_len]
dec_self_attns, dec_enc_attns = [], []
for layer in self.layers:
# dec_outputs: [batch_size, tgt_len, d_model], dec_self_attn: [batch_size, n_heads, tgt_len, tgt_len], dec_enc_attn: [batch_size, h_heads, tgt_len, src_len]
# Decoder的Block是上一个Block的输出dec_outputs(变化)和Encoder网络的输出enc_outputs(固定)
dec_outputs, dec_self_attn, dec_enc_attn = layer(dec_outputs, enc_outputs, dec_self_attn_mask,
dec_enc_attn_mask)
dec_self_attns.append(dec_self_attn)
dec_enc_attns.append(dec_enc_attn)
# dec_outputs: [batch_size, tgt_len, d_model]
return dec_outputs, dec_self_attns, dec_enc_attns
整体框架
class Transformer(nn.Module):
def __init__(self):
super(Transformer, self).__init__()
self.encoder = Encoder().to(device)
self.decoder = Decoder().to(device)
self.projection = nn.Linear(d_model, tgt_vocab_size, bias=False).to(device)
def forward(self, enc_inputs, dec_inputs):
"""Transformers的输入:两个序列
enc_inputs: [batch_size, src_len]
dec_inputs: [batch_size, tgt_len]
"""
# tensor to store decoder outputs
# outputs = torch.zeros(batch_size, tgt_len, tgt_vocab_size).to(self.device)
# enc_outputs: [batch_size, src_len, d_model], enc_self_attns: [n_layers, batch_size, n_heads, src_len, src_len]
# 经过Encoder网络后,得到的输出还是[batch_size, src_len, d_model]
enc_outputs, enc_self_attns = self.encoder(enc_inputs)
# dec_outputs: [batch_size, tgt_len, d_model], dec_self_attns: [n_layers, batch_size, n_heads, tgt_len, tgt_len], dec_enc_attn: [n_layers, batch_size, tgt_len, src_len]
dec_outputs, dec_self_attns, dec_enc_attns = self.decoder(dec_inputs, enc_inputs, enc_outputs)
# dec_outputs: [batch_size, tgt_len, d_model] -> dec_logits: [batch_size, tgt_len, tgt_vocab_size]
dec_logits = self.projection(dec_outputs)
return dec_logits.view(-1, dec_logits.size(-1)), enc_self_attns, dec_self_attns, dec_enc_attns