2016 级考研管理类联考数学真题

一、问题求解（本大题共 15 小题，每小题 3 分，共 45 分）下列每题给出 5 个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

真题（2016-01）-比例应用题

1.某家庭在一年的总支出中，子女教育支出与生活资料支出的比为 3：8，文化娱乐支出与子女教育支出的比为 1：2。已知文化娱乐支出占家庭总支出的 10.5%，则生活资料支出占家庭总支出的（ ）
A.40%
B.42%
C.48%
D.56%
E.64%

真题（2016-02）-几何-平面几何-正方形

2.有一批同规格的正方形瓷砖，用他们铺满整个正方形区域时剩余 180 块，将此正方形区域的边长增加一块瓷砖的长度时，还需要增加 21 块瓷砖才能铺满，该批瓷砖共有（ ）
A.9981 块
B.10000 块
C.10180 块
D.10201 块
E.10222 块

真题（2016-03）-比例应用题-路程

3.上午 9 时一辆货车从甲地出发前往乙地，同时一辆客车从乙地出发前往甲地，中午 12 时两车相遇，已知货车和客车的时速分别是 90 千米和 100 千米，则当客车到达甲地时，货车距乙地的距离是（ ）
A.30 千米
B.43 千米
C.45 千米
D.50 千米
E.57 千米

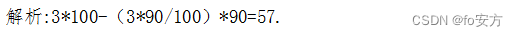
反向往返相遇，客车路程+货车路程=S，S=270+300=570，当客车到甲地：570÷100=5.7小时，货车也行程5.7小时，90×5.7=213，剩余570-213=57

真题（2016-04）-数据分析-概率

4.在分别标记了数字 1、2、3、4、5、6 的 6 张卡片中随机取 3 张，其上数字之和等于 10的概率为（ ）
A.0.05
B.0.1
C.0.15
D.0.2
E.0.25

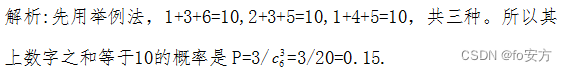
真题（2016-05）-应用题-比例

5.某商场将每台进价为 2000 元的冰箱以 2400 元销售时，每天销售 8 台，调研表明这种冰箱的售价每降低 50 元，每天就能多销售 4 台，若要每天销售利润最大，则该冰箱的定价应为（ ）元
A.2200
B.2250
C.2300
D.2350
E.2400

真题（2016-06）-

6.某委员会由三个不同专业的人员组成，三个专业的人数分别是 2、3、4，从中选派 2 位不同专业的委员外出调研，则不同的选派方式有（ ）
A.36 种
B.26 种
C.12 种
D.8 种
E.6 种

真题（2016-07）-

7.从 1 到 100 的整数中任取 1 个数，则该数能被 5 或 7 整除的概率为（ ）
A.0.02
B.0.14
C.0.2
D.0.32
E.0.34

真题（2016-08）-

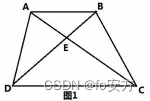
8.如图所示，在四边形 ABCD 中，AB//CD，AB 与 CD 的边长分别为 4 和 8.若△ABE 的面积为4，则四边形 ABCD 的面积为（ ）
A.24
B.30
C.32
D.36
E.40

真题（2016-09）-

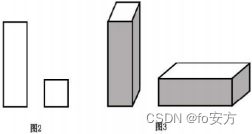
9.现有长方形木板 340 张，正方形木板 160 张（图 2）这些木板恰好可以装配成若干竖式和横式的无盖箱子（图 3），装配成的竖式和横式箱子的个数为（ ）
A.25，80
B.60，50
C.20，70
D.64，40
E.40，60

真题（2016-10）-

10.圆$x^2+y^2-6x+4y=0$上到原点距离最远的点是（ ）
A.（-3，2）
B.（3，-2）
C.（6，4）
D.（-6，4）
E.（6，-4）

真题（2016-11）-

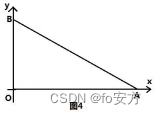
11.如图 4 所示，点 A B, O 的坐标分别为（4，0）、（0，3）、（0，0），若(x, y) 是AOB中的点，则2x  3y 的最大值为（ ）
A.6
B.7
C.8
D.9
E.12

真题（2016-12）-

12.设抛物线$y=x^2+2ax+b$与x 轴相交于 A, B 两点，点C 坐标为（0，2），若△ABC 的面积等于 6，则（ ）
A.$a^2-b=9$
B.$a^2+b=9$
C.$a^2-b=36$
D.$a^2+b=36$
E.$a^2-4b=9$

真题（2016-13）-

13.某公司以分期付款方式购买一套定价为 1100 万元的设备，首期付款 100 万元，之后每月付款 50 万元，并支付上期余款的利息，月利率 1%,该公司共为此设备支付了（ ）
A.1195 万元
B.1200 万元
C.1205 万元
D.1215 万元
E.1300 万元

真题（2016-14）-

14.某学生要在 4 门不同课程中选修 2 门课程，这 4 门课程中的 2 门各开设一个班，另外 2门各开设 2 个班，该学生不同的选课方式共有（ ）
A.6 种
B.8 种
C.10 种
D.13 种
E.15 种

真题（2016-15）-

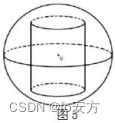
15.如下图，在半径为 10 厘米的球体上开一个底面半径是 6 厘米的圆柱形洞，则洞的内壁面积为（ ）（单位：平方厘米）
A.48π
B.288π
C.96π
D.576π
E.192π

二．条件充分性判断：（第 16-25 小题，每小题 3 分，共 30 分）

要求判断每题给出的条件（1）和（2）能否充分支持题干所陈述的结论，A、B、C、D、E 五个选项为判断结果，请选择一项符合试题要求的判断，请在答题卡上将所选的字母涂黑。
（A） 条件（1）充分，但条件（2）不充分
（B） 条件（2）充分，但条件（1）不充分
（C） 条件（1）和（2）都不充分，但联合起来充分
（D） 条件（1）充分，条件（2）也充分
（E） 条件（1）不充分，条件（2）也不充分，联合起来仍不充分

真题（2016-16）-

16.已知某公司男员工的平均年龄和女员工的平均年龄，则能确定该公司员工的平均年龄.
（1）已知该公司员工的人数
（2）已知该公司男、女员工的人数之比

真题（2016-17）-

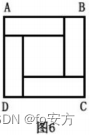
17.如图 6，正方形 ABCD 由四个相同的长方形和一个小正形拼成，则能确定小正方形的面积。
（1）已知正方形 ABCD 的面积
（2）已知长方形的长宽之比

真题（2016-18）-

18.利用长度为a和b 的两种管材能连接成长度为 37 的管道（单位：米）
（1）a = 3，b = 5
（2）a = 4，b = 6

真题（2016-19）-

19.设 x, y 是实数，则 x  6, y  4.
（1） $x\le y+2$
（2）$2y\le x+2$

真题（2016-20）-

20.将 2 升甲酒精和 1 升乙酒精混合，得到丙酒精，则能确定甲、乙两种酒精的浓度.
（1）1 升甲酒精和 5 升乙酒精混合后的浓度是丙酒精浓度的$\frac{1}{2}$倍
（2）1 升甲酒精和 2 升乙酒精混合后的中毒是丙酒精浓度的$\frac{2}{3}$倍

真题（2016-21）-

21.设两组数据$S_1$：3、4、5、6、7和$S_2$：4、5、6、7、a，则能确定a的值。
（1）$S_1$ 与$S_2$的均值相等
（2）$S_1$与$S_2$的方差相等

真题（2016-22）-

22.已知M 是一个平面有限点集，则平面上存在到M 中各点距离相等的点.
（1）M 中只有三个点
（2）M 中的任意三点都不共线

真题（2016-23）-

23.设 x, y 是实数，则可以确定$x^3+y^3$的最小值.
（1）xy=1
（2）x+y=2

真题（2016-24）-

24.已知数列$a_1,a_2,a_3,...,a_{10}$，则$a_1-a_2+a_3-...+a_9-a_{10}\ge 0$
（1）$a_n\ge a_{n+1},n=1,2,...,9$
（2）$a_n^2\ge a_{n+1}^2,n=1,2,...,9$

真题（2016-25）-

25.已知$f(x)=x^2+ax+b$，则$0\le f(1)\le 1$
（1） f (x) 在区间[ 0，1 ]中有两个零点
（2） f (x) 在区间[ 1，2 ]中有两个零点