目录
🌑🌑 背景
🌒 🌒作用
🌔🌔 问题
🌔🌔解决方案
🌙方法一
🌙方法二
🌝🌝我的解决方案
整理不易,欢迎一键三连!!!
送你们一条美丽的--分割线--
🌑🌑 背景
通常在安装某些模型或者模块时,通常最方便的方式就是通过pip install git+https://github.com/xxx/xxx的方式进行git clone,但是经常会由于网络问题没法正常正常下载,因此就需要本地下载编译安装。
🌒 🌒作用
pip install git+https://github.com/xxx/xxx命令的主要作用是:
pip将会使用Git工具自动从远程代码库中下载源代码并安装到本地目录下 ,并进行自动安装。
🌔🌔 问题
下载安装CLIP模型时,首先想到的是: pip install git+https://github.com/openai/CLIP.git的方式,然后下载过程中由于网络连接问题报错,因为服务器没法科学上网。。。
报错信息:Running command git clone --filter-blob:none --quiet https://github.com/openai/(lIgit /tmp/pip-reg-build-r7wizorc
fatal: 无法访间 "https://github.com/openai/(lIgit/':
Failed to comnect to github.com port 443 after 127334 ms: 连接超时
error:subprocess-exited with-error
详细报错如下:
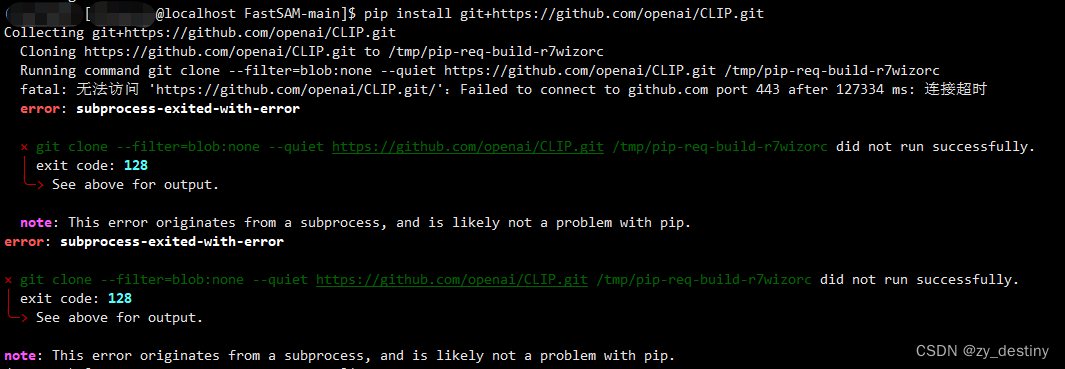
可以看到,报错信息中的提示也是说无法连接到GitHub网络,网络超时所以失败报错,但是如果实在想通过git+https这种方式安装,可以参考官方文档。pip documentation
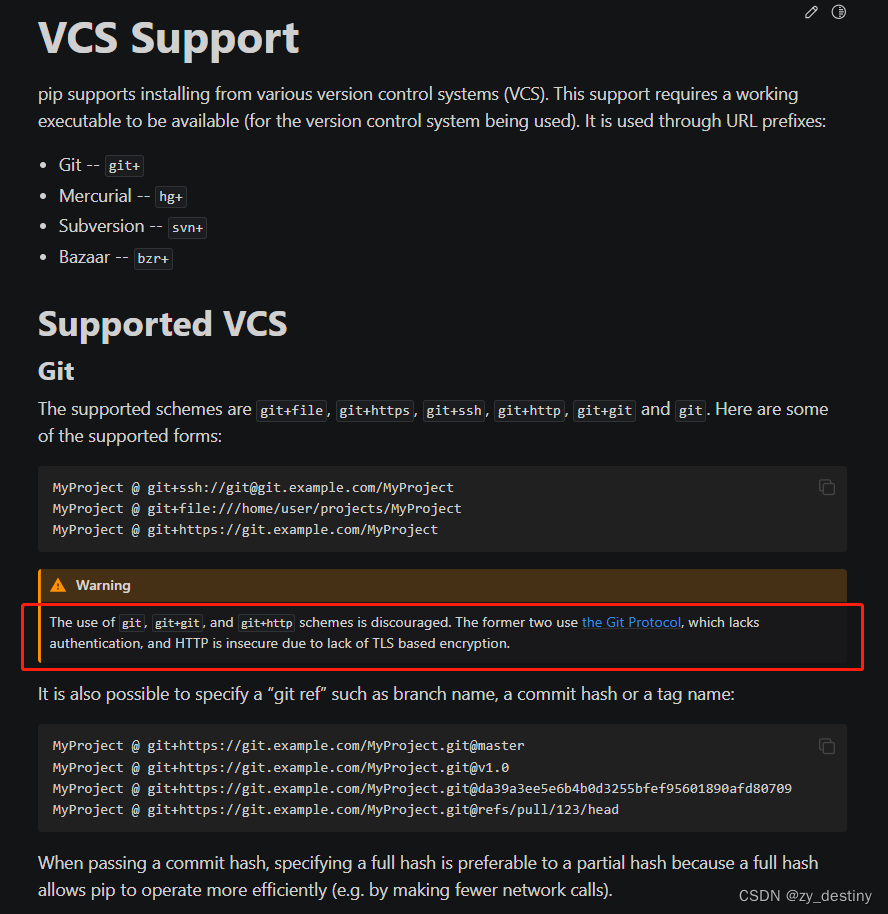
下面是官网的截图,可以看出其实官方是不推荐使用这种方式安装的。
🌔🌔解决方案
网上有多种解决方案,其中之一为修改命令:
🌙方法一
将原语句为:
pip install 'git+https://github.com/xxx/xxx.git'改为:
pip install 'git+https://gitclone.com/github.com/xxx/xxx.git'如果还不行,试试方法二,因为我的不行。。。
🌙方法二
清除防火墙或代理
git config --global --unset http.proxy
git config --global --unset https.proxy我试了2种方法都不行,所以我索性不用pip install git+https的方式了,一步一步来。
🌝🌝我的解决方案
- 第一步:直接打开要下载的GitHub网站,例如打开网站GitHub

- 第二步:下载zip压缩包,这一步需要点时间,如果你有科学上网的话会很快,因为都是代码,不会特别大,几秒钟就搞定了。

这一步如果还是无法下载的话,不妨试试以下代码:
#克隆源码
git clone https://github.com/xxx/xxx.git
如果可以的话,可以继续下一步。
- 第三步:解压zip,查看setup.py

至此恭喜你已经成功一大半了,只需最后一步。
- 第四步:运行以下代码实现本地编译安装
python setup.py install 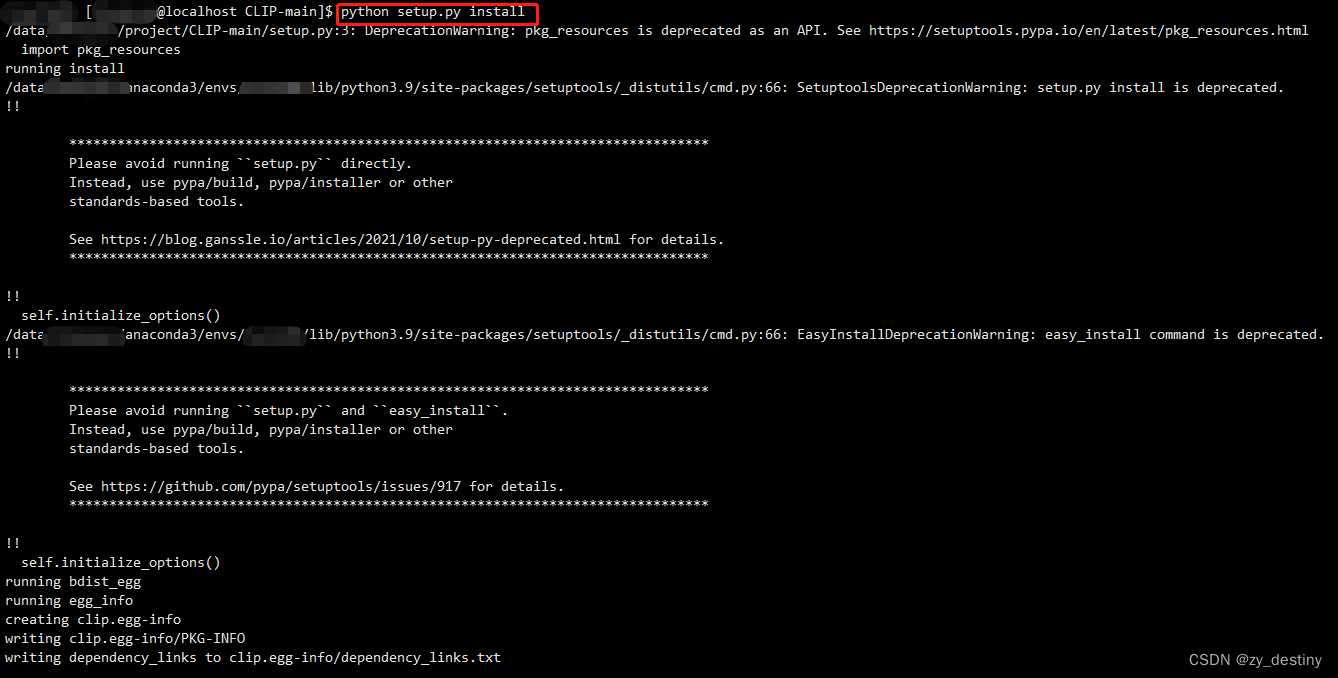
至此就大功告成了,撒花花🌸🌸🌸🌸
整理不易,欢迎一键三连!!!
送你们一条美丽的--分割线--
🌷🌷🍀🍀🌾🌾🍓🍓🍂🍂🙋🙋🐸🐸🙋🙋💖💖🍌🍌🔔🔔🍉🍉🍭🍭🍋🍋🍇🍇🏆🏆📸📸⛵⛵⭐⭐🍎🍎👍👍🌷🌷