一 分别用递归和非递归方式实现二叉树先序、中序和后序遍历
用递归和非递归方式,分别按照二叉树先序、中序和后序打印所有的节点。我们约定:先序遍历顺序为根、左、右;中序遍历顺序为左、根、右;后序遍历顺序为左、右、根。
递归方式
// 递归方式进行先序遍历
public void preorderRecursive(TreeNode root) {
if (root == null) return;
System.out.print(root.val + " "); // 打印当前节点
preorderRecursive(root.left); // 递归遍历左子树
preorderRecursive(root.right); // 递归遍历右子树
}
// 递归方式进行中序遍历
public void inorderRecursive(TreeNode root) {
if (root == null) return;
inorderRecursive(root.left); // 递归遍历左子树
System.out.print(root.val + " "); // 打印当前节点
inorderRecursive(root.right); // 递归遍历右子树
}
// 递归方式进行后序遍历
public void postorderRecursive(TreeNode root) {
if (root == null) return;
postorderRecursive(root.left); // 递归遍历左子树
postorderRecursive(root.right); // 递归遍历右子树
System.out.print(root.val + " "); // 打印当前节点
}非递归方式,用堆栈
public void preOrderUnRecur(Node head) {
System.out.println("pre-order:");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.println(head.value + " "); // 打印当前节点
// 先将右子节点入栈,再将左子节点入栈,保证弹出时的顺序是先左后右
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
public void inOrderUnRecur(Node head) {
System.out.println("in-order:");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left; // 将左子节点入栈
} else {
head = stack.pop();
System.out.println(head.value + " "); // 打印当前节点
head = head.right; // 遍历右子树
}
}
}
System.out.println();
}
public void posOrderUnRecur1(Node head) {
System.out.println("post-order:");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
// 先将右子节点入栈,再将左子节点入栈,保证弹出时的顺序是先左后右,进入s2时就是先右后左
if (head.right != null) {
s1.push(head.right);
}
if (head.left != null) {
s1.push(head.left);
}
}
while (!s2.isEmpty()) {
System.out.println(s2.pop().value + " "); // 打印当前节点
}
}
System.out.println();
}
public void posOrderUnRecur2(Node h) {
System.out.println("post-order:");
if (h != null) {
Stack<Node> s1 = new Stack<Node>();
s1.push(h);
Node cNode = null;
while (!s1.isEmpty()) {
cNode = s1.peek();
if (cNode.left != null && h != cNode.left && h != cNode.right) {
s1.push(cNode.left); // 将左子节点入栈
} else if (cNode.right != null && h != cNode.right) {
s1.push(cNode.right); // 将右子节点入栈
} else {
System.out.print(s1.pop().value + " "); // 打印当前节点
h = cNode;
}
}
}
System.out.println();
}这些函数都使用了栈来模拟递归过程。具体来说:
- preOrderUnRecur函数使用栈来模拟先序遍历的过程,先将根节点入栈,并在循环中弹出节点并打印,先将右子节点入栈,再将左子节点入栈。
- inOrderUnRecur函数使用栈来模拟中序遍历的过程,始终将左子节点入栈,直到没有左子节点,然后弹出节点并打印,再将右子节点入栈。
- posOrderUnRecur1函数使用两个栈来模拟后序遍历的过程,最终打印第二个栈中的节点,具体过程是先将根节点入栈1,然后循环中弹出节点并入栈2,先将左子节点入栈1,再将右子节点入栈1。
- posOrderUnRecur2函数使用单个栈来模拟后序遍历的过程,通过判断当前节点的左右子节点和上一个弹出的节点来确定是否打印当前节点
二 打印二叉树的边界节点
【题目】
给定一棵二叉树的头节点head,按照如下两种标准分别实现二叉树边界节点的逆时针打印。
标准一:1.头节点为边界节点。
2.叶节点为边界节点。3.如果节点在其所在的层中是最左的或最右的,那么该节点也是边界节点。
标准二:
1.头节点为边界节点。
2.叶节点为边界节点。
3.树左边界延伸下去的路径为边界节点。
4.树右边界延伸下去的路径为边界节点。例如,如图3-2所示的树。
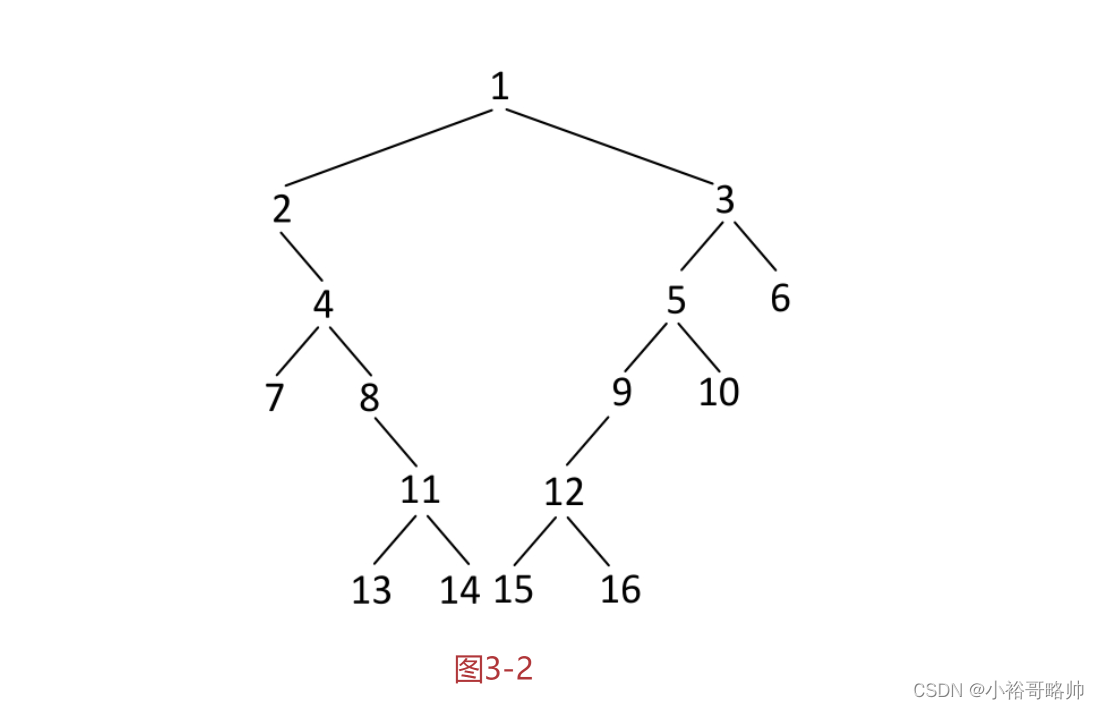
按标准一的打印结果为:
1,2,4,7,11,13,14,15,16,12,10,6,3
按标准二的打印结果为:1,2,4,7,13,14,15,16,10,6,3
【要求】
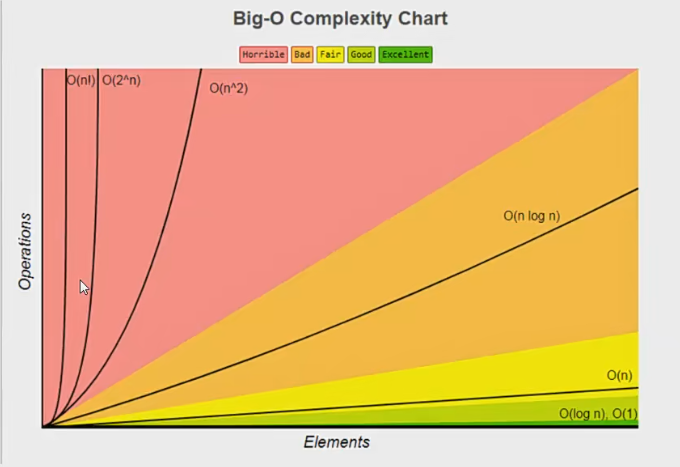
1.如果节点数为N,两种标准实现的时间复杂度要求都为O(N),额外空间复杂度要求都为O(h),h为二叉树的高度。
2.两种标准都要求逆时针顺序且不重复打印所有的边界节点。