✨个人主页: Yohifo
🎉所属专栏: 数据结构 | C语言
🎊每篇一句: 图片来源
- You can avoid reality, but you cannot avoid the consequences of avoiding reality.
- 你可以逃避现实,但你无法逃避其带来的后果。
文章目录
- 📘前言
- 📘正文
- 📖交换排序
- 📃冒泡排序
- 📃快速排序
- 🖋️快排(递归版)
- 💡霍尔版
- 💡挖坑法
- 💡双指针
- 🖋️快排(迭代版)
- 🖋️优化一、三数取中
- 🖋️优化二、小区间优化
- 🖋️优化三、三路划分
- 📖其他排序
- 📃归并排序
- 🖋️归并(递归版)
- 🖋️归并(迭代版)
- 📃计数排序
- 📖排序总结
- 📘总结
📘前言
排序(Sort)是初阶数据结构中的最后一块内容,所谓排序,就是通过某种手段,使目标数据变为递增或递减,排序有很多种方式:插入、选择、交换、归并、映射 等等,本文会介绍这些方式下的详细实现方法,因篇幅较长,故分为上下文的形式介绍,本文是下半部分。
下面是通过
排序生成的排行榜
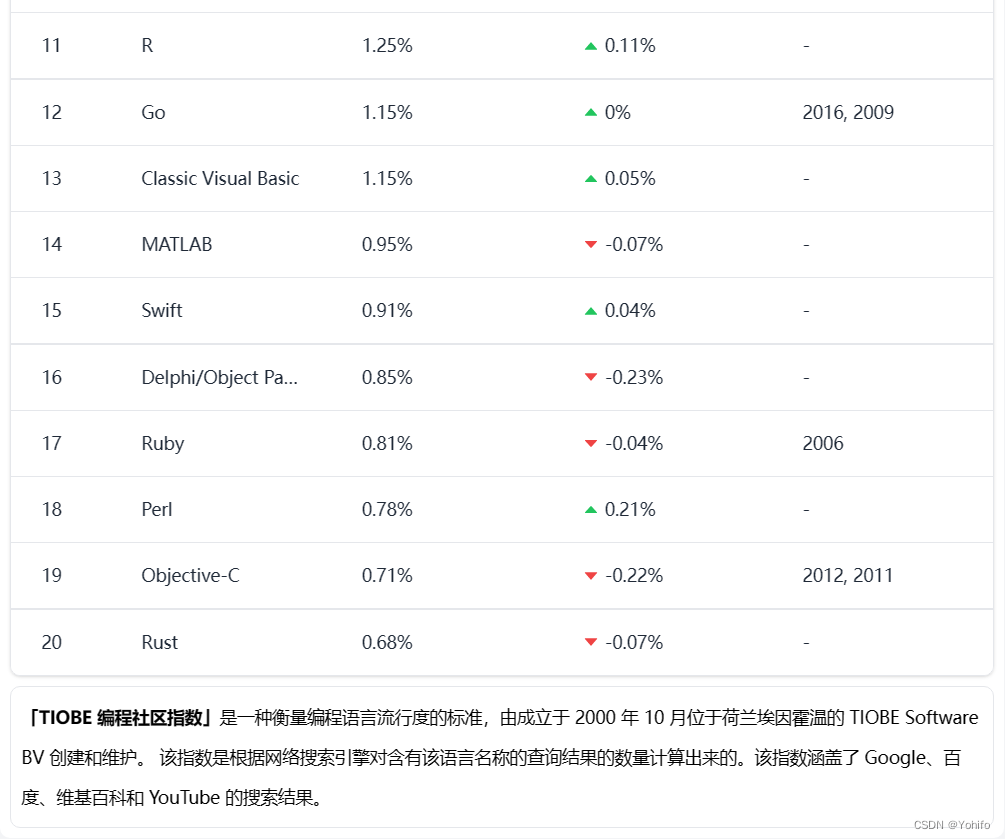
📘正文
📖交换排序
交换排序的核心在于交换,当两数符合交换条件时,就执行交换,通过不断的数据交换,实现数据间的有序性,交换排序中的代表之一就是有名的冒泡排序,另一个就是大名鼎鼎的快速排序,鉴于快速排序的重要性,它的相关介绍会非常多
📃冒泡排序
思想:将数据遍历 n-1 次,当前者大于后者时,就交换两个数,如此重复,直到数据有序
//冒泡排序
void BubbleSort(int* pa, int n)
{
assert(pa);
//思路:升序,当前值比后值大,就交换
for (int i = 0; i < n - 1; i++)
{
bool flag = true; //一个小优化,虽然没什么用
//冒泡的次数,与 i 挂钩
for (int j = 0; j < n - 1 - i; j++)
{
if (pa[j] > pa[j + 1])
{
swap(&pa[j], &pa[j + 1]);
flag = false;
}
}
if (flag)
break; //如果一次交换都没有出现,说明数组有序,直接结束
}
}
动图展示:
时间复杂度:
- 冒泡排序比较费时间,在大多数情况下需要将数据遍历 N^2 次,即
O(N^2)空间复杂度:
- 仅仅只需要一个
tmp变量辅助交换O(1)稳定性:
稳定,当两个相同数相遇时,两者相同,不执行交换程序,相对位置保持不变
📃快速排序
快排是本文的重头戏,光是实现方式就有三种,还有迭代版以及最后的三种优化方式,快排只有优化到位了,才能变成真正的快排(完全体)

🖋️快排(递归版)
递归版快排比较好写,但递归思想比较难想到,需要画出递归展开图辅助理解
注意: 众所周知,递归虽好,但是存在局限性,因为递归开辟的栈帧位于栈区,栈区空间是有限的,一旦排序数据量过大,会建立非常多的栈帧,从而引发栈溢出问题,因此当递归层次太深时,不推荐使用递归的方式实现

💡霍尔版
无论是什么版本的快排,都是遵循一个原则:选 key划分,选取一个 key ,使 key 左边的值小于等于 key ,右边的值大于 key ,这是快排的核心思想,霍尔(Hore)版的快排实现思想如下:
- 选取最左边的值为
key,比较时右边先走 - 因选的是左边,所以右边会先走(向左走),当右边在走的过程中遇到小于等于
key的值时停下 - 右边走完后,换左边走(向右走),当遇到大于
key的值时停止 - 此时交换左右两处的值
- 当左遇到右时(必定相遇,因为一次走一步),终止循环
- 执行最后一步,交换此时左(右)与
key值,此时就完成了需求:右边值 <=key< 左边值
以上是快排的单次实现,将排序这个大问题转成小问题,指定 begin 与 end ,当最后一步执行完后,可以从此时的 key 处分割出两块区域:[begin,key - 1]、key、[key + 1,end],将其中的两块区域传入函数,继续执行递归,当所有数据都排序完成后,快排就结束了
重难点:如果 key 选在最左边,那么右边先走;如果 key 选在最右边,左边先走。这样做的目的是保证最后一次交换时(左右重叠时与 key 值的交换)key 左边的数小于等于 key
//霍尔版
int PartSort1(int* pa, int begin, int end)
{
assert(pa);
GetMid(pa, begin, end); //这是三数取中,后面会提
//选 key 在左边,右边先走
int keyi = begin;
int lefti = begin;
int righti = end;
while (lefti < righti)
{
while (lefti < righti && pa[righti] > pa[keyi])
righti--;
while (lefti < righti && pa[lefti] <= pa[keyi])
lefti++;
swap(&pa[lefti], &pa[righti]);
}
swap(&pa[keyi], &pa[lefti]);
keyi = lefti;
return keyi;
}
//快速排序
void QuickSort(int* pa, int begin, int end)
{
assert(pa);
//思路:选出key,key 的右边小于key,key 的左边大于key
if (begin >= end)
return;
if ((end - begin + 1) < 20)
InsertSort(pa + begin, (end - begin + 1)); //这是小区间优化,后面会提
else
{
int keyi = PartSort1(pa, begin, end); //霍尔法
//int keyi = PartSort2(pa, begin, end); //挖坑法
//int keyi = PartSort3(pa, begin, end); //双指针法
//[begin, keyi - 1] keyi [keyi + 1, end]
QuickSort(pa, begin, keyi - 1);
QuickSort(pa, keyi + 1, end);
}
}
动图展示:
注意:为确保容易理解,这里直接选取优秀动图展示,动图来源
递归展开图:
💡挖坑法
思路:挖坑法核心思想与霍尔版一致,不过挖坑法为了便于理解,引入了坑位这个概念,简单来说就是先在 key 处挖坑,然后右边先走(假设 key 在最左边),找到小于等于 key 的值,就将此值放入到坑中,并在这里形成新坑;然后是左边走,同样的,找到值 -> 填入坑 -> 挖新坑,如此重复,直到左右相遇,此时的相遇点必然是一个未填充的坑,当然这个坑就是给 key 值准备的
//挖坑法
int PartSort2(int* pa, int begin, int end)
{
assert(pa);
GetMid(pa, begin, end); //这是三数取中,后面会提
//挖坑,先在key处挖坑,右边先走,找到小于等于key的,填入坑中,此处形成新坑
int key = pa[begin];
int lefti = begin;
int righti = end;
int holei = lefti; //坑位
while (lefti < righti)
{
while (lefti < righti && pa[righti] > key)
righti--;
pa[holei] = pa[righti]; //将当前值填入坑中
holei = righti; //挖新坑
while (lefti < righti && pa[lefti] <= key)
lefti++;
pa[holei] = pa[lefti];
holei = lefti;
}
pa[holei] = key;
return holei;
}
//快速排序
void QuickSort(int* pa, int begin, int end)
{
assert(pa);
//思路:选出key,key 的右边小于key,key 的左边大于key
if (begin >= end)
return;
if ((end - begin + 1) < 20)
InsertSort(pa + begin, (end - begin + 1)); //这里是小区间优化,后面会提
else
{
//int keyi = PartSort1(pa, begin, end); //霍尔法
int keyi = PartSort2(pa, begin, end); //挖坑法
//int keyi = PartSort3(pa, begin, end); //双指针法
//[begin, keyi - 1] keyi [keyi + 1, end]
QuickSort(pa, begin, keyi - 1);
QuickSort(pa, keyi + 1, end);
}
}
动图展示:
注意:为确保容易理解,这里直接选取优秀动图展示,动图来源
递归展开图与上面一致
💡双指针
思想:双指针的实现方式与上面两种截然不同,但最核心的思想仍是依赖 key,一样的先找 key,然后定义两个指针 prev 与 cur ,prev 的起始位置为 key ,而 cur 则是位于 prev 的下一位,判断 cur 处的值是否小于等于 key 值,如果是,则先 ++prev 后再交换 prev 与 cur 处的值,如此循环,直到 cur 移动至数据尾,最后一次交换为 key 与 prev 间的交换,交换完成后,就达到了快排的要求
//双指针法
int PartSort3(int* pa, int begin, int end)
{
assert(pa);
GetMid(pa, begin, end); //三数取中,后面会提
//思想:cur找比key小的,++prev后,交换
int* pKey = pa + begin;
int* prev = pKey;
int* cur = prev + 1;
int* pend = pa + end;
while (cur <= pend)
{
if (*cur <= *pKey)
swap(++prev, cur);
cur++;
}
swap(prev, pKey);
return prev - pa;
}
//快速排序
void QuickSort(int* pa, int begin, int end)
{
assert(pa);
//思路:选出key,key 的右边小于key,key 的左边大于key
if (begin >= end)
return;
if ((end - begin + 1) < 20)
InsertSort(pa + begin, (end - begin + 1)); //小区间优化,后面会提
else
{
//int keyi = PartSort1(pa, begin, end); //霍尔法
//int keyi = PartSort2(pa, begin, end); //挖坑法
int keyi = PartSort3(pa, begin, end); //双指针法
//[begin, keyi - 1] keyi [keyi + 1, end]
QuickSort(pa, begin, keyi - 1);
QuickSort(pa, keyi + 1, end);
}
}
动图展示:
注意:为确保容易理解,这里直接选取优秀动图展示,动图来源
递归展开图与上面一致
🖋️快排(迭代版)
前面说过,递归版快排 可能存在栈溢出问题。这时就需要使用迭代版快排,迭代版是借助栈来实现的,它不需要递归那样重复创建与销毁栈帧
分析:[begin ,end] 为一个大区间,借助递归是为了先使此区间的左边都比 key 小(等于),左边都比 key 大,当做完后,执行递归:[begin,key - 1] 为左半区间,[key + 1,end] 为右半区间;无论哪个区间,进入递归后都会形成新区间 [begin,end]
一顿分析下来不难发现,递归的目的是将区间不断细分,不断进行选 key 划分的操作,直到细分至1个元素或非法区间,递归就结束了,此时整组数据也都排好序了,下面来看看迭代版快排是如何实现的
思路:栈的特性是先进后出,我们可以先将最外层的区间值入栈,即将 begin 与 end 入栈,之后进行选 key 划分的操作,判断左右区间是否合法,合法才能入栈,继续循环,如果所有区间都非法,栈就空了,循环也就结束了
- 先将
begin与end入栈 - 取出栈中的值,得到一个区间 [
left,right] 注意:先取的是右边,因为栈的特性 - 根据此区间进行选
key划分,当操作结束后,记录下当前key的位置 - 判断
key - 1是否大于left,如果大于,说明左半区间合法,将left与key - 1入栈,后续将会形成新的区间 - 同理,判断
key + 1是否小于right,小于则说明右半区间合法,将区间值入栈 - 区间会生成区间,直到区间非法,直到所有的区间都非法,
栈也就空了,此时也就不需要进行排序操作了,整个迭代版快排也就结束了
注意: 需要借助栈,因此会用到栈的头文件与源文件,缺失的同学需自行添加
//快排,迭代版
void QuickSortNonR(int* pa, int begin, int end)
{
assert(pa);
//思路:利用栈的特性,先排序大范围,再排序小范围
Stack s;
StackInit(&s);
StackPush(&s, begin); //先将最开始的区间入栈
StackPush(&s, end);
while (!StackEmpty(&s))
{
int righti = StackTop(&s); //先取的是右,再取左
StackPop(&s);
int lefti = StackTop(&s);
StackPop(&s);
int keyi = (lefti + righti) / 2;
//小区间优化
if ((righti - lefti + 1) < 20)
InsertSort(pa + lefti, righti - lefti + 1);
else
keyi = PartSort3(pa, lefti, righti); //排序,调用双指针法
//判断是否符合条件入栈
if ((keyi + 1) < righti)
{
StackPush(&s, (keyi + 1));
StackPush(&s, righti); //这里入的是右,与前面呼应
}
if ((keyi - 1) > lefti)
{
StackPush(&s, lefti);
StackPush(&s, (keyi - 1)); 这里入的是右,与前面呼应
}
}
StackDestroy(&s);
}
动图展示:
无,上面这个迭代版核心部分调用的是双指针法进行选key划分,只不过将递归这个事情变成了入栈与出栈
未优化前的
快排都一样
时间复杂度:
- 如果数据接近顺序或接近逆序,所耗时间为
O(N^2),理想情况下为O(N*logN)空间复杂度:
- 递归是会耗费空间的,因此空间复杂度为
O(logN)稳定性:
不稳定,极有可能相同数中的后者与key交换,相对顺序被破坏
下面介绍针对排序的各种优化
🖋️优化一、三数取中
前面说过,接近有序或逆序的数据,对于快排是不太友好的,因为未优化前的快排选 key 始终是最右或最左,即有可能是最大或最小数,就像二分取中一样,快排只有尽可能取到中间数,才能发挥它的最大实力
因此我们可以借助一个函数:三数取中,分别取数据头、尾、中间进行比较,选取其中位于中间的数,再将其交换至数据首位(待会 key 取右边),经过这一优化后,快排的提升是非常明显的
//快排优化方案
//优化一、三数取中
void GetMid(int*pa, int begin, int end)
{
assert(pa);
int mid = (begin + end) / 2;
int midVali = begin; //假设最左值为中值
if (pa[midVali] > pa[mid])
{
//1.begin > mid > end
if (pa[mid] > pa[end])
midVali = mid;
//2.end > begin > mid
else if (pa[end] > pa[midVali])
midVali = begin;
//3.end = begin > mid
else
midVali = end;
}
else
{
//1.mid > begin > end
if (pa[end] < pa[midVali])
midVali = begin;
//2.end > mid > begin
else if (pa[mid] < pa[end])
midVali = mid;
else
midVali = end;
}
swap(&pa[begin], &pa[midVali]); //交换中间数至数据首
}
性能对比:
优化效果不言而喻,这个测试比较极端,有序组是绝对有序的,因此未加优化版快排是非常慢的
| 快排 | 排序50w数据(乱序) | 排序50w数据(有序) |
|---|---|---|
| 未加优化前的快排 | 耗时 154 ms | 耗时 111697 ms |
| 加三数取中后的快排 | 耗时 160 ms | 耗时 80 ms |
🖋️优化二、小区间优化
对于递归来说,越是接近小区间,所耗费时间就越长,越不利于排序,此时坚持使用快排是个不明智的选择,为此我们可以借助其他排序,弥补快排在小区间排序中的不足
这里借助的是直接插入排序,直接插入排序是个很不错的排序,稳定、速度也是中规中矩,小区间的定义取决于我们,我这里是将小于20的区间定义为小区间
//快速排序
void QuickSort(int* pa, int begin, int end)
{
assert(pa);
//思路:选出key,key 的右边小于key,key 的左边大于key
if (begin >= end)
return;
if ((end - begin + 1) < 20)
InsertSort(pa + begin, (end - begin + 1)); //这就是小区间优化
else
{
//int keyi = PartSort1(pa, begin, end); //霍尔法
//int keyi = PartSort2(pa, begin, end); //挖坑法
int keyi = PartSort3(pa, begin, end); //双指针法
//[begin, keyi - 1] keyi [keyi + 1, end]
QuickSort(pa, begin, keyi - 1);
QuickSort(pa, keyi + 1, end);
}
}
同样放个性能对比:
这里默认加了三数取中,小区间优化不像三数取中那样明显,但加了总比没加好
| 快排 | 排序50w数据(乱序) | 排序50w数据(有序) |
|---|---|---|
| 未加小区间优化前的快排 | 耗时 162 ms | 耗时 86 ms |
| 加小区间优化后的快排 | 耗时 107 ms | 耗时 66 ms |
🖋️优化三、三路划分
接下来介绍快排的完全版本:三路划分
分析:部分数据中存在多个与 key 相等的值,如果按照以前的快排方式,会有很多重复操作,因此我们需要将与 key 相等的值集中在中间,形成中路,比 key 小的放在其左边,大的放在其右边。这样会形成 左、中、右 三路数据,大大提高了快排速度
思路:三路划分的核心在于控制中路的左右边界,这里需要借助三个变量:lefti、righti、curi,显然 lefti 位于 begin 处,righti 位于 end 处,curi 位于 begin + 1 处。实现起来也很简单:
- 判断当前
curi处值是否大于key,大于就将其与righti处的值交换,然后righti--扩大右路 - 之后再判断
curi是否小于key,小于就与lefti交换,此时lefti++扩大左路,curi也需要+1,因为curi一开始是在lefti的下一个,lefti动,curi也要跟着动,不然它就被覆盖了 - 如果
curi既不大于key,也不小于key,说明它等于key,此时将curi处的值划入中路,不需要交换,直接curi++就行了 - 如此重复,直到
curi大于righti,显然此时有三条路,[begin,lefti]、[lefti+1,righti-1]、[righti,end] 这就是三路划分
//优化三、三路划分
//将与key相同的值,分到中间,避免过多key而导致的性能下降
//FV的意思是完全版本
void QuicSortFV(int* pa, int begin, int end)
{
assert(pa);
if (begin >= end)
return;
if ((end - begin + 1) < 20)
InsertSort(pa + begin, end - begin + 1);
else
{
GetMid(pa, begin, end);
int key = pa[begin];
int lefti = begin;
int righti = end;
int curi = begin + 1;
while (curi <= righti)
{
if (pa[curi] > key)
swap(&pa[curi], &pa[righti--]); //扩大右路
else if (pa[curi] < key)
swap(&pa[curi++], &pa[lefti++]); //扩大左路
else
curi++; //此时等于key,扩大中路的范围就行了
}
QuicSortFV(pa, begin, lefti - 1);
QuicSortFV(pa, righti + 1, end);
}
}
注意: 此时的三数取中需要进行优化,不再取最右、中间、最左 这三个位置的数,而是取 最右、随机位置、最右,改进的原因是排序OJ题有些测试用例会搞事情,引入随机位置这个概念后,快排适应性会更强,当然,优化后的三数取中任然可以用于优化其他版本的快排
//int mid = (begin + end) / 2; //之前的三数取中,mid 取的是中间位
int mid = begin + rand() % (end - begin); //mid 取随机位置
性能展示:
这里借助力扣中的一道中等题:排序数组,来展示展示完全版快排的实力
注:只有优化拉满的快排才能通过这道题,关键点之一就是三数取中取随机位置,也就是它的测试用例搞事情,迭代版快排也可以升级为完全版,返回一个数组,只将左右两路入栈就行了
📖其他排序
快排已经结束了,现在来说说其他排序:归并与计数,归并也是个很优秀的排序,稳定、快速,而计数是整数排序里的王者,要说他们有什么缺点,可能就是比较耗时间了
📃归并排序
归并排序的核心思想:合并两个有序数组,合并后数组就有序了
归并:回归与合并
归并排序多用于外排序,即对磁盘中的大数据进行排序

🖋️归并(递归版)
思路:首先要得到左右皆有序的数组,然后合并,显然这个需要借助递归实现,将大问题化小问题:将原数据分为左右两个区间,交给递归让他们变得有序,最后再执行有序数组合并。依靠递出,区间会慢慢变小,直到区间内只有两个数,执行合并,然后逐渐向上回归,回归的过程就是不断合并的过程,数据最开始的左右区间会逐渐变得有序,当回归到第一层时,执行最后一次有序数组合并,数据整体就变得有序了
注意: 归并排序需要借助额外空间,将合并的数据先放在额外空间中,再通过内存拷贝的方式拷贝回原数组
//归并排序
void _MergeSort(int* pa, int begin, int end, int* tmp)
{
assert(pa && tmp);
//思路:令数组左右两边有序,然后合并两个有序数组
if (begin >= end)
return;
int mid = (begin + end) / 2; //分成左右两个区间进行递出
_MergeSort(pa, begin, mid, tmp); //递归左半区间
_MergeSort(pa, mid + 1, end, tmp); //递归右半区间
//下面是合并有序数组部分
int left1 = begin; //左半区间左边界
int right1 = mid; //左半区间右边界
int left2 = mid + 1; //右半区间左边界
int right2 = end; //右半区间右边界
int pos = begin; //这是额外空间的下标,会随着递归层度而变化
while (left1 <= right1 && left2 <= right2)
{
//升序,取小的放前面
if (pa[left1] <= pa[left2])
tmp[pos++] = pa[left1++];
else
tmp[pos++] = pa[left2++];
}
//确保合并完成
while (left1 <= right1)
tmp[pos++] = pa[left1++];
while (left2 <= right2)
tmp[pos++] = pa[left2++];
//将额外空间中的数据拷贝回原数组中
memcpy(pa + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* pa, int n)
{
assert(pa);
int* tmp = (int*)malloc(sizeof(int) * n); //额外辅助空间
assert(tmp);
_MergeSort(pa, 0, n - 1, tmp); //归并主程序
free(tmp); //记得释放
tmp = NULL;
}
动图展示:
注意:为确保容易理解,这里直接选取优秀动图展示,动图来源
时间复杂度:
- 归并也是二分的思想
O(N*logN)空间复杂度:
- 归并还需要额外空间,因此空间复杂度为
O(N + logN)稳定性:
稳定,合并数组的过程中,两个相同数的相对位置不会被改变,因为前者总是比后者先并入数组
🖋️归并(迭代版)
归并也有迭代版,它不像快排那样借助栈,只需要定义一个范围 rangeN ,默认为1,将这个 rangeN 套入循环中,对 rangN 范围内的数据进行合并,rangeN 会逐渐扩大,直到其 >= n,此时范围非法,整个迭代版归并排序就完成了
//归并,迭代版
void MergeSortNonR(int* pa, int n)
{
assert(pa);
//思路:通过一个变量来控制归并范围,范围从1开始,到n-1结束
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
int rangeN = 1; //范围从1开始
while (rangeN < n)
{
for (int i = 0; i < n; i += rangeN * 2)
{
//第一组
int begin1 = i;
int end1 = i + rangeN - 1;
//第二组
int begin2 = i + rangeN;
int end2 = i + rangeN * 2 + 1;
//迭代版需要考虑边界问题,不能越界
if (end1 >= n)
break; //左半区间的右边界越界,直接跳出(只有一个数组,也没有合并的必要)
else if (begin2 >= n)
break; //右半区间的左边界越界,也是直接跳出(右半区间非法)
else if (end2 >= n)
end2 = n - 1; //右半区间的右边界越界,将其矫正至 n - 1 处,不能跳出,否则会有数据遗漏
//因为是迭代,需要面面俱到
int pos = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (pa[begin1] <= pa[begin2])
tmp[pos++] = pa[begin1++];
else
tmp[pos++] = pa[begin2++];
}
//确保数据合并完成
while (begin1 <= end1)
tmp[pos++] = pa[begin1++];
while (begin2 <= end2)
tmp[pos++] = pa[begin2++];
memcpy(pa + i, tmp + i, sizeof(int) * (end2 - i + 1)); //一块一块的拷贝
}
rangeN *= 2;
}
free(tmp);
tmp = NULL;
}
注意: 迭代版归并存在很严重的边界问题,如果不加以判断,那么肯定会发生越界问题,可以通过判断解决问题
方案一、直接跳出
注意: 采取直接跳出的话,只能将额外空间中的数据逐块拷贝回原数组,即在for循环中进行拷贝;如果整体拷贝,即在for循环外进行拷贝,是会出现问题的
//迭代版需要考虑边界问题,不能越界
if (end1 >= n)
break; //左半区间的右边界越界,直接跳出(只有一个数组,也没有合并的必要)
else if (begin2 >= n)
break; //右半区间的左边界越界,也是直接跳出(右半区间非法)
else if (end2 >= n)
end2 = n - 1; //右半区间的右边界越界,将其矫正至 n - 1 处,不能跳出,否则会有数据遗漏
方案二、修正范围
修正范围不像直接跳出那样讲究,逐块拷贝或整体拷贝都是可行的
//修正范围不会跳出循环
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)
end2 = n - 1;

时间复杂度:
- 归并也是二分的思想
O(N*logN)空间复杂度:
- 迭代版不用递归,归并还需要额外空间,因此空间复杂度为
O(N)稳定性:
稳定,合并数组的过程中,两个相同数的相对位置不会被改变,因为前者总是比后者先并入数组
📃计数排序
计数排序又称非比较排序,计数排序的核心思想是映射,将待排序数据映射到辅助空间中的对应位置,这个位置的值,就是当前下标(即被映射值)的出现次数,当所有数据都被映射到辅助空间中后,把辅助空间遍历一遍,如果当前位置有值,就将下标值赋给原数组,直到当前位置为空,当辅助空间遍历结束后,计数排序就结束了
优化:采取相对映射,尽可能减小空间浪费
//计数排序
void CountSort(int* pa, int n)
{
assert(pa);
//思路:映射,将所有数映射到一片空间中,依次拷贝即可
int max = pa[0];
int min = pa[0];
//找最大值与最小值
for (int i = 1; i < n; i++)
{
if (pa[i] > max)
max = pa[i];
if (pa[i] < min)
min = pa[i];
}
//相对映射,空间绝对够用,因为是 最大值-最小值+1
int* mapSpace = (int*)malloc(sizeof(int) * (max - min + 1)); //辅助空间
assert(mapSpace);
memset(mapSpace, 0, sizeof(int) * (max - min + 1)); //初始化为0
for (int i = 0; i < n; i++)
mapSpace[pa[i] - min]++; //将数据映射到辅助空间中
int j = 0; //控制原数组的下标,需要单独定义
for(int i = 0 ; i < (max - min + 1);i++)
{
//需要把当前位置清空
while (mapSpace[i]--)
pa[j++] = i + min; //拷贝至原数组
}
free(mapSpace); //释放原空间
mapSpace = NULL;
}

时间复杂度:
- 对于整数来说,计数是绝对的王者,无非就是将数据遍历了三遍,因此为
O(N)空间复杂度:
- 需要开辟辅助空间
O(Max - Min + 1)稳定性:
不稳定,计数排序数据都是直接覆盖的注意:
- 计数排序适用于数据较为集中,且为整数的数据
- 绝对映射是直接根据最大值 + 1来开辟空间,很是浪费
📖排序总结
说明:快排与归并采用的都是递归版
| 排序名称 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 直接插入排序 | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(1) | 不稳定 |
| 简单选择排序 | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*logN) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(1) | 稳定 |
| 快速排序 | O(N*logN) | O(logN) | 不稳定 |
| 归并排序 | O(N*logN) | O(N+logN) | 稳定 |
| 计数排序 | O(N) | O(Max-Min+1) | 不稳定 |
来看看各种排序的性能表现(10w无序数据):
说明:快排(完全版+递归),归并(递归)

📘总结
排序有很多种,有好的、有坏的,我们要重点掌握优秀的排序,比如希尔和堆排,当前其他排序的思想也得清楚,知道怎么实现就行了。排序界有三位大哥:希尔、快排、归并,关于快排C语言有专门的库函数qsort实现,这个函数优化极佳,是最快的快排。
如果你觉得本文写的还不错的话,期待留下一个小小的赞👍,你的支持是我分享的最大动力!
如果本文有不足或错误的地方,随时欢迎指出,我会在第一时间改正

…
相关文章推荐
带你学懂数据结构中的八大排序(上)
关于“堆”,看看这篇文章就够了(附堆的两种应用场景)
听说你还不了解二叉树?赶紧进来轻松解决

















![洛谷千题详解 | P1029 [NOIP2001 普及组] 最大公约数和最小公倍数问题【C++语言】](https://img-blog.csdnimg.cn/2e1e7732091a4ca2bedf44ddd08f252e.png)