题目描述

汉诺塔是约19世纪末，在欧州的商店中出售一种智力玩具。它的结构如下图所示：
 

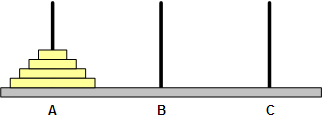
在一个平板上立有三根铁针，分别记为A, B, C。开始时，铁针 A 上依次叠放着从大到小 n 个圆盘，游戏的目标就是将 A 上的 n 个圆盘全部转移到 C 上，要求每次只能移动某根铁针最上层一个圆盘，圆盘不得放在这三根铁针以外的任何地方，而且永远只能将小的圆盘叠放在大的圆盘之上。

例如，下面就是示例输出中（n = 3）移动方案的图示：

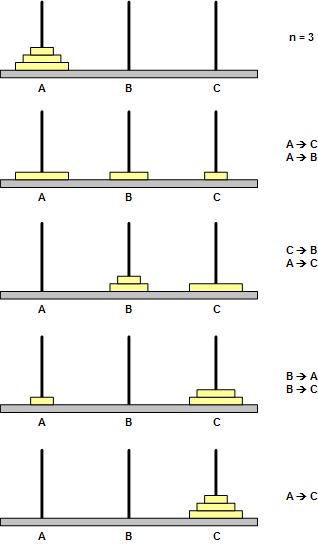
这是一个著名的问题，几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘，且不允许大盘放在小盘上面，所以 64 个盘的移动次数是：
18,446,744,073,709,551,615
这是一个天文数字，若每一微秒可能做一次移动，那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小 n 值时的汉诺塔，但很难用计算机解决64层的汉诺塔。

关于输入

输入数据只有一个正整数 n (n <= 16) ， 表示开始时铁针 A 上的圆盘数

关于输出

要求输出步数最少的搬动方案，方案是由若干个步骤构成的，输出的每行就表示一个移动步骤，例如，“A->B”就表示把铁针 A 最上层的一个圆盘移动到 B 上。

代码实现

#include <iostream>
using namespace std;

void move(char a,char b){
    cout<<"盘子从"<<a<<"移动到"<<b<<endl;
}

void f(int n,char a,char b,char c){
    if(n==1){
        move(a,c);
        count++;
        return;
    }
    else{
        f(n-1,a,c,b);
        move(a,c);
        count++;
        f(n-1,b,a,c);
    }
}

int main() {
	int n; cin>>n;
	f(n,'A','B','C');
	return 0;
}