题目描述
这是 LeetCode 上的 「2304. 网格中的最小路径代价」 ,难度为 「中等」。
Tag : 「最短路」、「图」、「模拟」、「序列 DP」、「动态规划」
给你一个下标从 0 开始的整数矩阵 grid,矩阵大小为 m x n,由从 0 到
的不同整数组成。
你可以在此矩阵中,从一个单元格移动到下一行的任何其他单元格。
如果你位于单元格 ,且满足 ,你可以移动到 , , ..., 中的任何一个单元格。注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为
,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的值之和加上所有移动的代价之和 。从第一行任意单元格出发,返回到达最后一行任意单元格的最小路径代价。
示例 1: 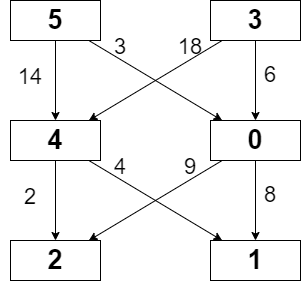
输入:grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出:17
解释:最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。
示例 2:
输入:grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出:6
解释:
最小代价的路径是 2 -> 3 。
- 路径途经单元格值之和 2 + 3 = 5 。
- 从 2 移动到 3 的代价为 1 。
路径总代价为 5 + 1 = 6 。
提示:
-
-
-
-
grid由从0到m * n - 1的不同整数组成 -
-
-
建新图 + 建虚拟点 + 堆优化 Dijkstra
❝注意:可以直接使用解法二的方法,但先认真看完本做法,再去看解法二,会有相当丝滑的体验。
❞
每次移动,「实际路径权值 = 经过边的权值 + 目的地的权值」。
利用原图,构建新图:「每个单元格视为一个点,除最后一行外,每个点对下一行的所有点连一条有向边,边权 = 原图中该边的权值 + 原图中该目的地的权值」。
分析新图中的点边数量:
-
点:共 个点,数量为 -
边:不算最后一行,共 个点,这些点与下一行的每个点均有一条有向边,合计 条边,数量为
原问题转换为:求点 到 的最短路,其中点 所在位置为第 行,点 所在位置为第 行。
这似乎是一个「多源汇最短路」问题?但求解多源汇最短路的 Floyd 算法是
的,会超时。
实际上,我们也并不真的关心图中任意点之间的最短路,仅仅关心第一行到最后一行的最短路。
因此,「我们可通过建立“虚拟源点”和“虚拟汇点”的方式,来将“多源汇最短路”问题转换为“单源最短路”问题。」
具体的,我们创建一个“虚拟源点”,该点向所有第一行的点连权值为 的有向边;同时创建一个“虚拟汇点”,最后一行的所有点向该点连权值为 的有向边。
问题进一步转化为:求“虚拟源点”到“虚拟汇点”的最短路。
至此,我们通过 「建新图 -> 创建虚拟源汇点(转换为单源最短路)-> 套用单源最短路算法」 解决本题。
将新图中点的数量记为
,边数记为
,朴素 Dijkstra 复杂度为
,堆优化的 Dijkstra 的复杂度为
,当
(相对稀疏)时,优先使用堆优化 Dijkstra。
Java 代码:
class Solution {
int N = 50 * 50 + 2, M = 50 * 50 * 50, idx = 0, n;
int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
public int minPathCost(int[][] grid, int[][] moveCost) {
int N = grid.length, M = grid[0].length;
int S = N * M, T = S + 1;
n = N * M + 2;
Arrays.fill(he, -1);
//「虚拟源点」向「第一行」进行连边
for (int i = 0; i < M; i++) add(S, grid[0][i], grid[0][i]);
// 转换原图
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < M; j++) {
int a = grid[i][j];
for (int k = 0; k < M; k++) {
int b = grid[i + 1][k];
add(a, b, moveCost[a][k] + b);
}
}
}
//「最后一行」向「虚拟汇点」进行连边
for (int i = 0; i < M; i++) add(grid[N - 1][i], T, 0);
// 最短路
int[] dist = dijkstra(S);
return dist[T];
}
int[] dijkstra(int x) {
// 起始先将所有的点标记为「未更新」和「距离为正无穷」
int[] dist = new int[n];
Arrays.fill(dist, 0x3f3f3f3f);
boolean[] vis = new boolean[n];
dist[x] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (点编号, 到起点的距离) 进行存储,优先弹出「最短距离」较小的点
PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[1]-b[1]);
q.add(new int[]{x, 0});
while (!q.isEmpty()) {
// 每次从「优先队列」中弹出
int[] poll = q.poll();
int u = poll[0], step = poll[1];
// 如果弹出的点被标记「已更新」,则跳过
if (vis[u]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = true;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
q.add(new int[]{j, dist[j]});
}
}
return dist;
}
}
C++ 代码:
class Solution {
public:
static const int N = 50 * 50 + 2, M = 50 * 50 * 50;
int he[N], e[M], ne[M], w[M], idx, n, INF = 0x3f3f3f3f;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int N = grid.size(), M = grid[0].size();
int S = N * M, T = S + 1;
n = N * M + 2;
fill(he, he + n, -1);
//「虚拟源点」向「第一行」进行连边
for (int i = 0; i < M; i++) add(S, grid[0][i], grid[0][i]);
// 转换原图
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < M; j++) {
int a = grid[i][j];
for (int k = 0; k < M; k++) {
int b = grid[i + 1][k];
add(a, b, moveCost[a][k] + b);
}
}
}
//「最后一行」向「虚拟汇点」进行连边
for (int i = 0; i < M; i++) add(grid[N - 1][i], T, 0);
// 最短路
vector<int> dist = dijkstra(S);
return dist[T];
}
vector<int> dijkstra(int x) {
vector<int> dist(n, 0x3f3f3f3f);
vector<bool> vis(n, false);
dist[x] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (到起点的距离, 点编号) 进行存储,优先弹出「最短距离」较小的点
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({0, x});
while (!q.empty()) {
// 每次从「优先队列」中弹出
auto [step, u] = q.top();
q.pop();
// 如果弹出的点被标记「已更新」,则跳过
if (vis[u]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = true;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
q.push({dist[j], j});
}
}
return dist;
}
};
Python 代码:
import heapq
class Solution:
def minPathCost(self, grid, moveCost):
N, M = len(grid), len(grid[0])
S, T = N * M, N * M + 1
n = N * M + 2
he = [-1] * n
e, ne, w = [-1] * (50 * 50 * 50), [-1] * (50 * 50 * 50), [-1] * (50 * 50 * 50)
idx = 0
def add(a, b, c):
nonlocal idx
e[idx] = b
ne[idx] = he[a]
w[idx] = c
he[a] = idx
idx += 1
def dijkstra(x):
dist = [float('inf')] * n
vis = [False] * n
dist[x] = 0
# 使用「优先队列」存储所有可用于更新的点
# 以 (到起点的距离, 点编号) 进行存储,优先弹出「最短距离」较小的点
q = [(0, x)]
heapq.heapify(q)
while q:
# 每次从「优先队列」中弹出
step, u = heapq.heappop(q)
# 如果弹出的点被标记「已更新」,则跳过
if vis[u]: continue
# 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = True
i = he[u]
while i != -1:
j, c = e[i], w[i]
i = ne[i]
if dist[j] <= dist[u] + c: continue
dist[j] = dist[u] + c
heapq.heappush(q, (dist[j], j))
return dist
#「虚拟源点」向「第一行」进行连边
for i in range(M):
add(S, grid[0][i], grid[0][i])
# 转换原图
for i in range(N - 1):
for j in range(M):
a = grid[i][j]
for k in range(M):
b = grid[i + 1][k]
add(a, b, moveCost[a][k] + b)
#「最后一行」向「虚拟汇点」进行连边
for i in range(M):
add(grid[N - 1][i], T, 0)
# 最短路
dist = dijkstra(S)
return dist[T]
-
时间复杂度: ,其中 为新图中的点数 , 为新图中的边数 -
空间复杂度:
堆优化 Dijkstra
什么?你说你实在不想建新图,也不想搞什么虚拟点,就想用你心爱的 BFS 来做?!
我懂你意思,但那不叫 BFS。
只是将「建新图」和「建虚拟点」的过程省掉,仍需要使用优先队列(堆)来每次取出当前“路径代价最小”的点来进行扩充,执行过程仍为堆优化 Dijkstra 的核心操作。
尤其所谓“省掉” 建新图 和 建虚拟点,真就字面上的“省掉”,并非不存在,因为两种做法思路是完全一致的。可简单列举「本解法」与「解法一」的对应关系:
-
起始往队列放入首行元素,对应了解法一的“建立虚拟源点”过程; -
从队列中取元素出来扩充时,若当前元素所在行是最后一行时,用当前路径代价来更新答案,对应了解法一的“建立虚拟汇点”过程; -
扩充时直接遍历列(即下一行的所有点),对应的解法一的“用原图边建新图”的过程。
Java 代码:
class Solution {
public int minPathCost(int[][] grid, int[][] moveCost) {
int m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
int[][] dist = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) dist[i][j] = INF;
}
PriorityQueue<int[]> d = new PriorityQueue<>((a,b)->a[2]-b[2]);
for (int i = 0; i < n; i++) {
d.add(new int[]{0, i, grid[0][i]});
dist[0][i] = grid[0][i];
}
while (!d.isEmpty()) {
int[] info = d.poll();
int x = info[0], y = info[1], cur = info[2];
if (x == m - 1) {
ans = Math.min(ans, cur);
continue;
}
for (int i = 0; i < n; i++) {
int step = moveCost[grid[x][y]][i], ne = grid[x + 1][i];
int tot = cur + step + ne;
if (tot >= ans || dist[x + 1][i] <= tot) continue;
dist[x + 1][i] = tot;
d.add(new int[]{x + 1, i, tot});
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size(), n = grid[0].size(), INF = 0x3f3f3f3f, ans = INF;
vector<vector<int>> dist(m, vector<int>(n, INF));
priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
for (int i = 0; i < n; i++) {
pq.push({0, i, grid[0][i]});
dist[0][i] = grid[0][i];
}
while (!pq.empty()) {
vector<int> info = pq.top();
pq.pop();
int x = info[0], y = info[1], cur = info[2];
if (x == m - 1) {
ans = min(ans, cur);
continue;
}
for (int i = 0; i < n; i++) {
int step = moveCost[grid[x][y]][i], ne = grid[x + 1][i];
int tot = cur + step + ne;
if (tot >= ans || dist[x + 1][i] <= tot) continue;
dist[x + 1][i] = tot;
pq.push({x + 1, i, tot});
}
}
return ans;
}
};
Python 代码:
class Solution:
def minPathCost(self, grid, moveCost):
m, n, INF = len(grid), len(grid[0]), float('inf')
ans = INF
dist = [[INF] * n for _ in range(m)]
for i in range(n):
dist[0][i] = grid[0][i]
pq = [(0, i, grid[0][i]) for i in range(n)]
while pq:
x, y, cur = heapq.heappop(pq)
if x == m - 1:
ans = min(ans, cur)
continue
for i in range(n):
step, ne = moveCost[grid[x][y]][i], grid[x + 1][i]
tot = cur + step + ne
if tot >= ans or dist[x + 1][i] <= tot: continue
dist[x + 1][i] = tot
heapq.heappush(pq, (x + 1, i, tot))
return ans
-
时间复杂度: ,其中 为新图中的点数 , 为新图中的边数 -
空间复杂度:
原地模拟
什么?你说你连图论的方法都不想用,想就着题意做一遍?
可以。甚至当你调整更新方向,还能利用已有的 grid,实现原地模拟。
具体的,我们将“从上往下走”调整为“从下往上走”,这样可以确保当我们使用底下一行 来更新当前行 时,所用到的 不会被覆盖。
Java 代码:
class Solution {
public int minPathCost(int[][] grid, int[][] moveCost) {
int m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
for (int i = m - 2; i >= 0; i--) {
for (int j = 0; j < n; j++) {
int cur = INF;
for (int k = 0; k < n; k++) cur = Math.min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (int i = 0; i < n; i++) ans = Math.min(ans, grid[0][i]);
return ans;
}
}
C++ 代码:
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size(), n = grid[0].size(), INF = INT_MAX, ans = INF;
for (int i = m - 2; i >= 0; i--) {
for (int j = 0; j < n; j++) {
int cur = INF;
for (int k = 0; k < n; k++) cur = min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (int i = 0; i < n; i++) ans = min(ans, grid[0][i]);
return ans;
}
};
Python 代码:
class Solution:
def minPathCost(self, grid, moveCost):
m, n = len(grid), len(grid[0])
for i in range(m - 2, -1, -1):
for j in range(n):
grid[i][j] += min([grid[i + 1][k] + moveCost[grid[i][j]][k] for k in range(n)])
return min([grid[0][i] for i in range(n)])
TypeScript 代码:
function minPathCost(grid: number[][], moveCost: number[][]): number {
let m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
for (let i = m - 2; i >= 0; i--) {
for (let j = 0; j < n; j++) {
let cur = INF;
for (let k = 0; k < n; k++) cur = Math.min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (let i = 0; i < n; i++) ans = Math.min(ans, grid[0][i]);
return ans;
};
-
时间复杂度: ,其中 和 分别代表给定 grid的长宽 -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2304 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉