dt=0.01;
tout=200; %总时间为2
x=zeros(1,tout);
x(1)=0.5; %初始位置
mu=0.2; sigma=1;
Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wt
for t=1:tout-1
    x(t+1)=x(t)+mu*x(t)*dt+sigma*x(t)*Wt(t);
end
t1=1:10:tout; %对原时间序列进行抽样
xt=zeros(1,length(t1));
i=1;
for t=t1
    xt(i)=0.5*exp((mu-0.5*sigma^2).*dt*t+ ...
        sigma*sum(Wt(1:t))); %使用理论解对原序列进行抽样计算
    i=i+1;
end
plot(dt*(1:tout),x,LineWidth=1.5)
hold on
plot(dt*t1,xt,LineWidth=1.5)
hold off
xlabel("$t$",FontSize=20,Interpreter="latex")

dt=0.01;
tout=200;
n=10000;
tends=zeros(1,n);
x=zeros(1,tout);
x(1)=0.1;
mu=0.2; sigma=1;
for k=1:n
    Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wt
    for t=1:tout-1
        x(t+1)=x(t)+mu*x(t)*dt+sigma*x(t)*Wt(t);
    end
    tends(k)=x(end);
end
histogram(tends,200)

dt=0.01;
tout=200;
x=zeros(1,tout);
x(1)=0; %初始位置
mu=5; sigma=2;
for i=1:5
    Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wt
    for t=1:tout-1
        x(t+1)=x(t)-mu*x(t)*dt+sigma*Wt(t);
    end
    plot(dt*(1:tout),x,LineWidth=1.5)
    hold on
end
xlabel("$t$",FontSize=20,Interpreter="latex")
hold off

dt=0.01;
tout=200;
x=zeros(1,tout);
x(1)=0; %初始位置
mu=5; sigma=2;
tends=zeros(1,100000);
for i=1:100000
    Wt=sqrt(dt)*randn(1,tout); %产生随机序列Wt
    for t=1:tout-1
        x(t+1)=x(t)-mu*x(t)*dt+sigma*Wt(t); %Langevin方程
    end
    tends(i)=x(end);
end
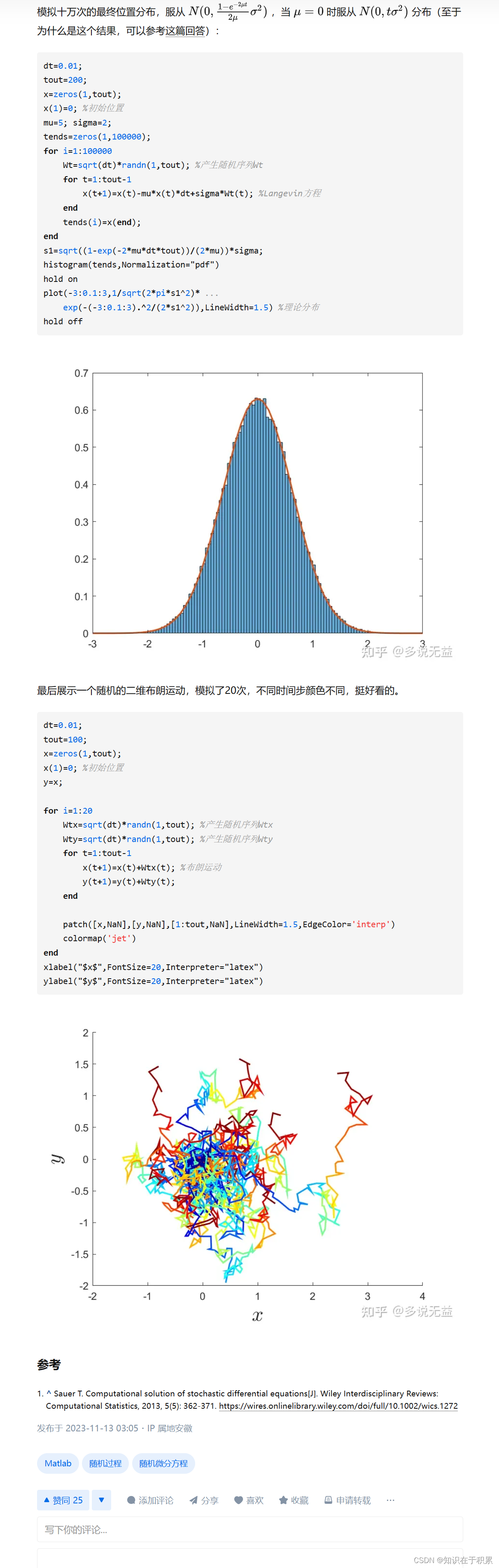
s1=sqrt((1-exp(-2*mu*dt*tout))/(2*mu))*sigma;
histogram(tends,Normalization="pdf")
hold on 
plot(-3:0.1:3,1/sqrt(2*pi*s1^2)* ...
    exp(-(-3:0.1:3).^2/(2*s1^2)),LineWidth=1.5) %理论分布
hold off

dt=0.01;
tout=100;
x=zeros(1,tout); 
x(1)=0; %初始位置
y=x;

for i=1:20
    Wtx=sqrt(dt)*randn(1,tout); %产生随机序列Wtx
    Wty=sqrt(dt)*randn(1,tout); %产生随机序列Wty
    for t=1:tout-1
        x(t+1)=x(t)+Wtx(t); %布朗运动
        y(t+1)=y(t)+Wty(t);
    end
    
    patch([x,NaN],[y,NaN],[1:tout,NaN],LineWidth=1.5,EdgeColor='interp')
    colormap('jet')
end
xlabel("$x$",FontSize=20,Interpreter="latex")
ylabel("$y$",FontSize=20,Interpreter="latex")

^Sauer T. Computational solution of stochastic differential equations[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2013, 5(5): 362-371. https://wires.onlinelibrary.wiley.com/doi/full/10.1002/wics.1272

详见知乎：https://zhuanlan.zhihu.com/p/666480835?utm_campaign=&utm_medium=social&utm_oi=1315073218793488384&utm_psn=1710572578152996864&utm_source=qq