题目
463. 岛屿的周长
简单
相关标签
深度优先搜索 广度优先搜索 数组 矩阵
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1:
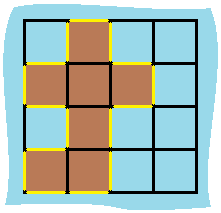
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出:16 解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
输入:grid = [[1]] 输出:4
示例 3:
输入:grid = [[1,0]] 输出:4
提示:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100grid[i][j]为0或1
思路和解题方法
定义方向数组:在类的开头,定义了一个大小为4x2的二维数组direction。该数组中存储了四个方向的偏移量,用于表示上、下、左、右四个方向。
islandPerimeter函数:这是计算岛屿周长的主要函数。它接受一个二维网格作为输入,并返回岛屿的周长。
嵌套循环遍历网格:通过两个嵌套循环,遍历整个二维网格。外层循环迭代行,内层循环迭代列。
检查陆地格子:如果当前格子是陆地(grid[i][j] == 1),则进入下一步计算周长的操作。
遍历四个方向:对于每个陆地格子,使用一个循环遍历四个方向。通过对方向数组进行迭代,分别计算出当前格子上、下、左、右四个方向的相邻格子的坐标。
判断边界条件:对于每个相邻格子的坐标(x, y),判断是否满足以下条件之一:
- x<0 或 x>=grid.size() 或 y<0 或 y>=grid[0].size():相邻格子超出了网格边界,即该方向对应的边界算作岛屿的边界。
- grid[x][y] == 0:相邻格子是水域,即该方向对应的边界算作岛屿的边界。
计算周长:对于每个满足边界条件的方向,将周长ans加一。
返回结果:返回最终计算得到的岛屿周长ans。
复杂度
时间复杂度:
O(m*n)
时间复杂度为O(m*n),其中m是二维网格的行数,n是二维网格的列数。因为代码中使用了两层嵌套循环来遍历整个二维网格。
空间复杂度
O(1)
空间复杂度为O(1),因为除了定义了一个常量大小的二维数组来表示四个方向的偏移量之外,没有使用额外的空间。
c++ 代码
class Solution {
public:
int direction[4][2] = {0,1,1,0,-1,0,0,-1}; // 定义一个二维数组表示四个方向的偏移量
int islandPerimeter(vector<vector<int>>& grid) {
int ans= 0; // 初始化周长计数器为 0
for(int i= 0;i<grid.size();i++) // 遍历二维网格的行
{
for(int j= 0 ;j<grid[0].size();j++) // 遍历二维网格的列
{
if(grid[i][j] == 1) // 如果当前格子是陆地(即值为 1)
{
for(int k = 0;k<4;k++) // 遍历四个方向
{
int x= i+direction[k][0] ; // 计算相邻格子的行坐标
int y = j+direction[k][1]; // 计算相邻格子的列坐标
if(x<0||x>=grid.size()||y<0||y>=grid[0].size()||grid[x][y] == 0)
{
ans++; // 如果相邻格子是水域或者超出边界,则将周长加 1
}
}
}
}
}
return ans; // 返回计算得到的总周长
}
};附Java代码
class Solution {
// 定义方向数组,分别表示向右、向下、向左、向上移动的偏移量
static int[] dx = {0, 1, 0, -1};
static int[] dy = {1, 0, -1, 0};
public int islandPerimeter(int[][] grid) {
int n = grid.length; // 获取二维网格的行数
int m = grid[0].length; // 获取二维网格的列数
int ans = 0; // 初始化岛屿周长为0
for (int i = 0; i < n; ++i) { // 遍历二维网格的每一行
for (int j = 0; j < m; ++j) { // 遍历二维网格的每一列
if (grid[i][j] == 1) { // 如果当前格子是陆地
int cnt = 0; // 初始化当前格子的周长计数为0
for (int k = 0; k < 4; ++k) { // 遍历当前格子的上下左右四个方向
int tx = i + dx[k]; // 计算相邻格子的行坐标
int ty = j + dy[k]; // 计算相邻格子的列坐标
// 判断相邻格子是否超出网格边界或者是水域,如果是则周长加1
if (tx < 0 || tx >= n || ty < 0 || ty >= m || grid[tx][ty] == 0) {
cnt += 1;
}
}
ans += cnt; // 将当前格子的周长计数累加到总周长中
}
}
}
return ans; // 返回计算得到的岛屿周长
}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。