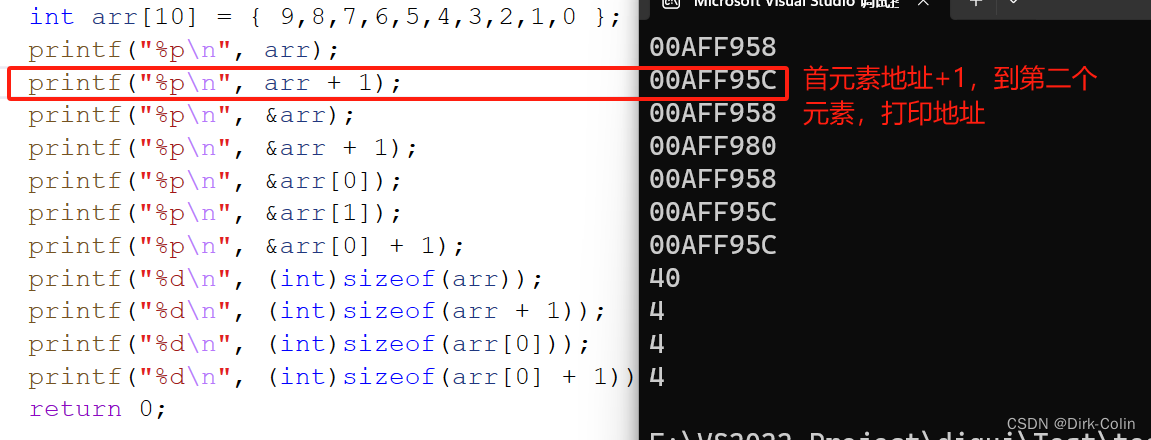
通过分歧进行自我监督探索
0、问题
使用可微的ri直接去更新动作策略的参数的,那是不是就不需要去计算价值函数或者critic网络了?
1、Motivation
高效的探索是RL中长期存在的问题。以前的大多数方式要么陷入具有随机动力学的环境,要么效率太低,无法扩展到真正的机器人设置。
2、Introduction
然而,在学习无噪声模拟环境之外的预测模型时,有一个关键的挑战:如何处理代理-环境交互的随机性? 随机性可能由以下几个来源引起:(1)嘈杂的环境观察(例如,电视播放噪声);(2)智能体动作执行中的噪声(例如,滑动);(3)作为智能体动作输出的随机性(例如,智能体抛硬币)。
尽管有几种方法可以在低维状态空间中构建随机模型,但将其扩展到高维输入(例如图像)仍然具有挑战性。另一种方法是建立确定性模型,但在随机不变的特征空间中对输入进行编码。最近的工作提出在逆模型特征空间中构建这样的模型,它可以处理随机观测,但当代理本身是噪源时(例如带有遥控器的电视)会失败。
文章提出训练前向动力学模型的集合,并激励智能体探索该集合中模型预测之间存在最大分歧或方差的动作空间。
3、方法
该模型利用预测的不确定性来激励策略访问不确定性最大的状态。
本文模型的核心思想是:歧义。
模型利用采样到的transitions,训练一批前向模型:
{
f
θ
1
,
f
θ
2
…
,
f
θ
k
}
\{f_{\theta_1},f_{\theta_2}\ldots,f_{\theta_k}\}
{fθ1,fθ2…,fθk}
这个前向模型与ICM中的forward dynamics model一致,通过最小化loss来更新参数:
l
o
s
s
=
∥
f
(
x
t
,
a
t
;
θ
)
−
x
t
+
1
∥
2
loss=\begin{aligned}\|f(x_t,a_t;\theta)-x_{t+1}\|_2\end{aligned}
loss=∥f(xt,at;θ)−xt+1∥2
而本文提出的歧义的核心思想是,对于智能体已经很好地探索过的状态空间,将会收集到足够的数据来训练所有模型,从而导致模型之间的一致,而对于新领域和未探索的领域,所有模型仍然具有很高的预测误差,从而导致对下一个状态预测的分歧。
本文模型将intrinsic reward定义为这种分歧,即不同模型的输出之间的方差:
r
t
i
≜
E
θ
[
∥
f
(
x
t
,
a
t
;
θ
)
−
E
θ
[
f
(
x
t
,
a
t
;
θ
)
]
∥
2
2
]
\begin{aligned}r_t^i\triangleq\mathbb{E}_\theta\Big[\|f(x_t,a_t;\theta)-\mathbb{E}_\theta[f(x_t,a_t;\theta)]\|_2^2\Big]\end{aligned}
rti≜Eθ[∥f(xt,at;θ)−Eθ[f(xt,at;θ)]∥22]
在实践中,为了所有的预测目的,我们将状态x编码到嵌入空间φ(x)中。
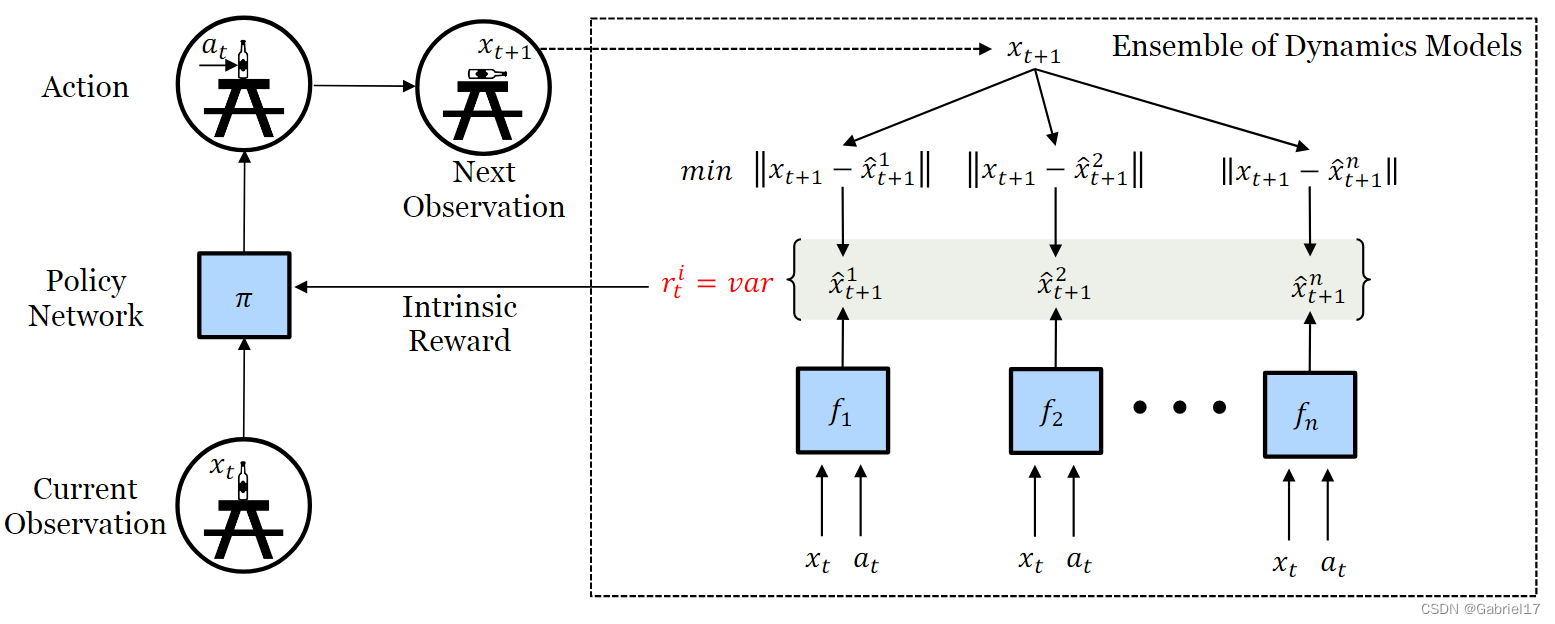
本文提出的智能体代理是自我监督的,不需要任何外部奖励来进行探索。
本文方法与ICM不同,ICM在足够大的样本后,将趋于平均值。由于均值不同于个体的真实随机状态,预测误差仍然很高,使得智能体永远对随机行为感到好奇。
本模型提出的内在奖励作为一个可微函数,以便使用似然最大化来执行策略优化,这很像监督学习而不是强化学习。来自模型的内在奖励可以非常有效地通知智能体在前向预测损失高的方向改变其行动空间,而不是像强化学习那样提供标量反馈。纯粹是基于当前状态和智能体预测动作的模型集合的心理模拟。
与其通过PPO (RL)最大化期望中的内在奖励,我们可以通过将ri 视为可微损失函数来使用直接梯度来优化策略参数θ:
min
θ
1
,
…
,
θ
k
(
1
/
k
)
∑
i
=
1
k
∥
f
θ
i
(
x
t
,
a
t
)
−
x
t
+
1
∥
2
\begin{aligned}\min_{\theta_1,\dots,\theta_k}&(1/k)\sum_{i=1}^k\|f_{\theta_i}(x_t,a_t)-x_{t+1}\|_2\end{aligned}
θ1,…,θkmin(1/k)i=1∑k∥fθi(xt,at)−xt+1∥2
max θ P ( 1 / k ) ∑ i = 1 k [ ∥ f θ i ( x t , a t ) − ( 1 / k ) ∑ j = 1 k f θ j ( x t , a t ) ∥ 2 2 ] \begin{aligned}\max_{\theta_P}&(1/k)\sum_{i=1}^k\left[\|f_{\theta_i}(x_t,a_t)-(1/k)\sum_{j=1}^kf_{\theta_j}(x_t,a_t)\|_2^2\right]\end{aligned} θPmax(1/k)i=1∑k[∥fθi(xt,at)−(1/k)j=1∑kfθj(xt,at)∥22]
a t = π ( x t ; θ P ) a_t=\pi(x_t;\theta_P) at=π(xt;θP)
4、实验
实验包括三个部分:a)验证在标准非随机环境下的性能; B)在过渡动力学和观测空间中具有随机性的环境的比较; c)验证我们的目标所促进的可微分政策优化的效率。
- 设计实验测试了Disagreement方法在标准非随机环境下的性能。比较了雅达利游戏的近确定性和非随机标准基准的不同内在奖励公式。基于分歧的方法优于最先进的方法,而不会在非随机情况下失去准确性。
- 在随机性较高的环境下进行测试,基于集合的分歧方法在智能体看到足够的样本后,收敛到几乎为零的内在奖励,而基于预测误差的模型在收敛时也会为具有较高随机性的观测值(即标签为1的图像)分配更多的奖励。基于分歧的方法在存在随机性的情况下表现更好。
- 实验显示可微探索加速了智能体的学习,表明了直接梯度优化的有效性。现在在短期和大结构的行动空间设置中评估仅可微分探索(无强化)的性能。
实验显示可微探索加速了智能体的学习,表明了直接梯度优化的有效性。现在在短期和大结构的行动空间设置中评估仅可微分探索(无强化)的性能。 - 在真实世界的机器手臂实验上,基于分歧的可微分策略优化探索展示出了极高的性能。