n−皇后问题是指将 n 个皇后放在 n×n的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
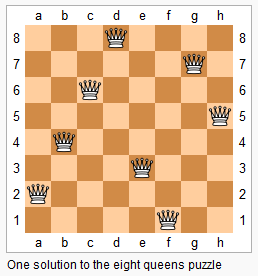
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
国际象棋中的皇后可以直接攻击到她所在的行,列,斜方向上的棋子
思路:这道题也是使用DFS来求解的,关于DFS与递归的问题可以先看我的上一篇文章,有图解:排列数字(DFS深度优先搜索)-CSDN博客
一开始想的办法就是遍历枚举每一种情况,第一行第一列放皇后,之后如何,第二行第二列放皇后,之后如何,但是这样太繁琐了。
不妨每次只看一行的情况,遍历这一行上的每一列,如果当前位置可以放则放下皇后,然后进入下一行,再次枚举放皇后,直到每一行都放好了皇后,这时候便得到了一种可行的摆法,最开始是第一行第一列放皇后,得到解之后或者位置矛盾就回溯(return和if循环),第一行第二列放皇后,以此类推。
回溯则是从终止的那一列开始的(已经输出或者位置矛盾不能放),因为每一列都有一个for循环,所以当前列终止之后会自动执行上一列的for循环(如果还能循环的话),也就是我们所谓的回到上一列继续枚举,如果全部执行完毕就得到了全部结果。

这是DFS的代码:
void dfs(int u) //u表示行,输出每一行皇后的位置
{
if( u == n ) //到最后一个位置的下一位(所有位置都填满了)
{
for(int i=0;i<n;i++) puts(g[i]); //输出第i行的棋盘状态,g是二维数组,这样是按行输出
puts("");
return;
}
for(int i=0;i<n;i++) //对于一行,枚举每一列的情况
{
//行是u,列是i
//dg下标n-u+i,udg下标u+i,如果下标相同就说明是同一条对角线
if(!col[i] && !dg[n+u-i] && !udg[u+i]) //如果这一列没有放过,对角线和反对角线也没有放过
{
g[u][i]='Q'; //在当前的位置放上皇后
col[i] = dg[n+u-i] = udg[u+i] = true; //记录当前位置已经被使用
dfs(u+1); //全部处理好后进入下一层
col[i] = dg[n+u-i] = udg[u+i] = false; //回溯的时候要恢复
g[u][i]='.'; //回溯要把这个位置的皇后去掉
}
}
}输出的时候是按行输出
if( u == n ) //到最后一个位置的下一位(所有位置都填满了)
{
for(int i=0;i<n;i++) puts(g[i]); //输出第i行的棋盘状态,g是二维数组,这样是按行输出
puts("");
return;
}对于二维数组 g,可以通过 g[i] 访问到第 i 行的字符串,因为二维数组在内存中是按行存储的连续空间。
在 C++ 中,二维数组可以看作是一维数组的数组。对于 g 这样的二维数组,g[i] 表示的是第 i 个一维数组的起始地址,即第 i 行的地址。由于数组名就是该数组的首地址,因此可以直接使用 g[i] 来表示第 i 行。
其中
if(!col[i] && !dg[n+u-i] && !udg[u+i])这个判断条件是检查在当前点g[u][i]上的竖列,正对角线和反对角线上是否有皇后(因为我们是一行一行的输入,然后按列枚举皇后在当前行的摆法,所以不用判断行上有没有其他皇后)。
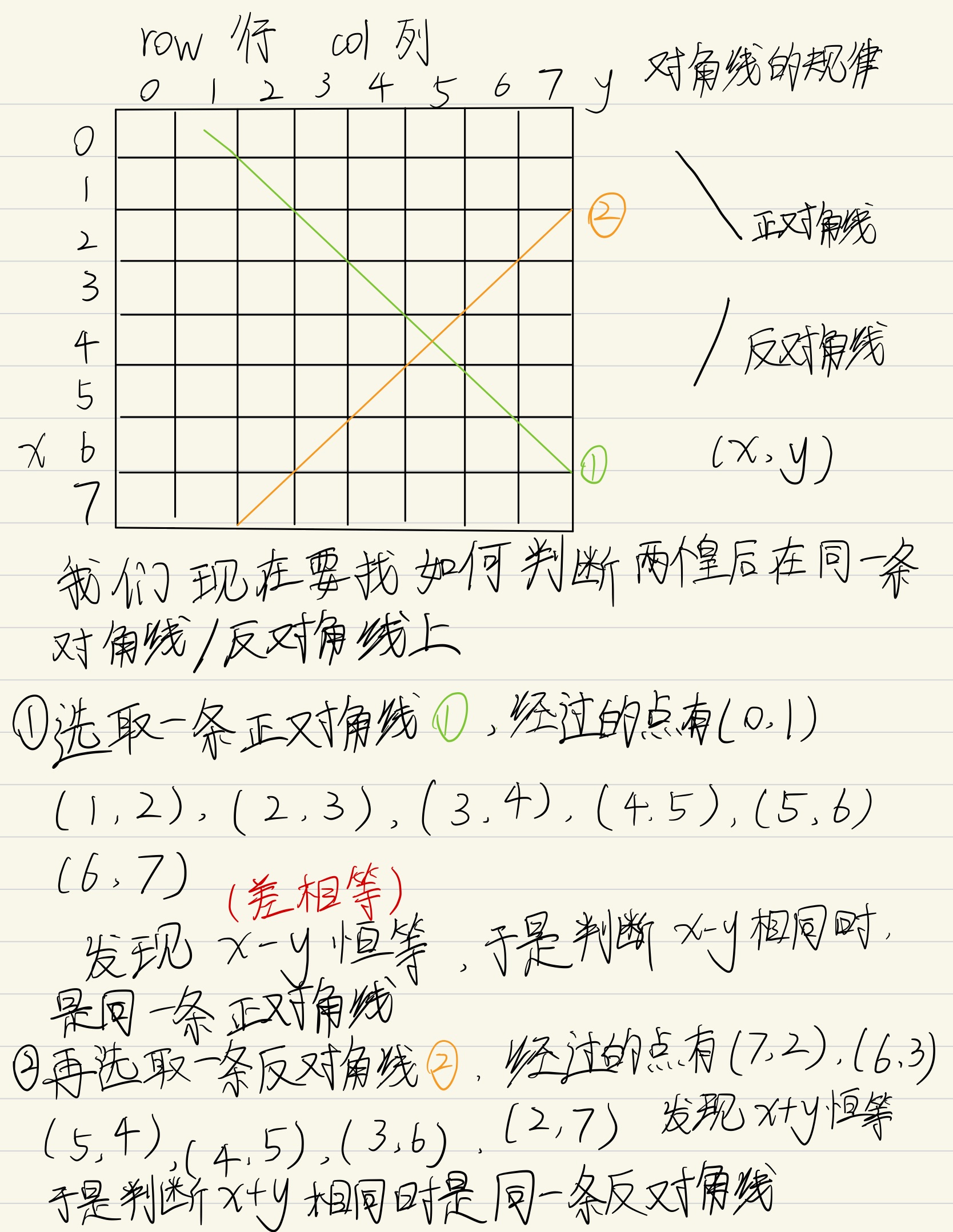
dg和udg的下标可能较难理解,如果图中的点位置用(x,y)表示x行y列,那么这里的u对应行,i对应列,也就是(u,i)表示当前点的位置,这里画图可知道同一条反对角线上,u+i是一样的,而同一条正对角线上,u-i是一样的,但是因为这里用下标表示第几条正对角线,下标不能为负,所以我们加上一个n使下标为正数(加上之后不影响下标表达,比如原来正对角线的下标有-3,-1,2,7,我们加上一个n=4之后就变为1,3,6,11,实际上每个下标还是分开的能映射到对应的正对角线)

示例代码:
#include<iostream>
using namespace std;
const int N=20; //对角线是格子的两倍长
char g[N][N]; //记录棋盘状态信息
bool col[N],dg[N*2],udg[N*2]; //col列,dg记录正对角线的占用情况,udg记录负对角线的占用
int n;
void dfs(int u) //u表示行,输出每一行皇后的位置
{
if( u == n ) //到最后一个位置的下一位(所有位置都填满了)
{
for(int i=0;i<n;i++) puts(g[i]); //输出第i行的棋盘状态,g是二维数组,这样是按行输出
puts("");
return;
}
for(int i=0;i<n;i++) //对于一行,枚举每一列的情况
{
//行是u,列是i
//dg下标n-u+i,udg下标u+i,如果下标相同就说明是同一条对角线
if(!col[i] && !dg[n+u-i] && !udg[u+i]) //如果这一列没有放过,对角线和反对角线也没有放过
{
g[u][i]='Q'; //在当前的位置放上皇后
col[i] = dg[n+u-i] = udg[u+i] = true; //记录当前位置已经被使用
dfs(u+1); //全部处理好后进入下一层
col[i] = dg[n+u-i] = udg[u+i] = false; //回溯的时候要恢复
g[u][i]='.'; //回溯要把这个位置的皇后去掉
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
g[i][j]='.'; //初始化,棋盘全部为'.'
}
}
dfs(0); //从第0行开始看
}关于代码运行的流程:n=4的情况




注意:不仅是return有回溯到上一列的效果,当进入递归中,上一列的for循环也是可以让当前列回溯到上一列。