1.线性回归从0实现

从0开始实现整个方法，包括数据流水线、模型、损失函数和小批量随机梯度下降优化器
（1）导入需要的包

% matplotlib inline
import random
import torch
from d2l import torch as d2l  #pip install d2l torch torchvision

（2）构造数据

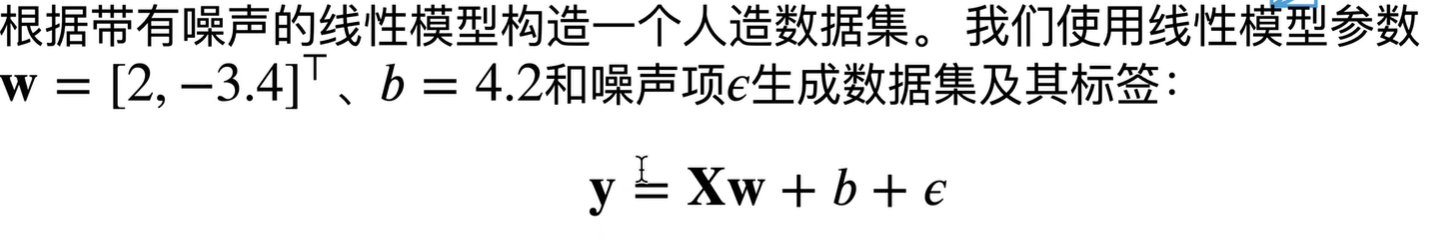
def synthetic_data(w,b,num_examples):
    """生成y = Xw + b + 噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))  #生成均值为0，方差为1的随机数X，大小为:num个样本，列数为len(w)
    Y = torch.matmul(X, w) + b
    Y += torch.normal(0, 0.01, Y.shape) # 噪音
    return X, Y.reshape((-1,1))  #将X，Y以列向量的形式返回

true_w = torch.tensor([2,-3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:',features[0], '\nlabel:',labels[0])

（3）定义一个data_iter函数，该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量

def data_iter(batch_size, features, labels):
    num_examples = len(features) #样本数量
    indices = list(range(num_examples))  # 每个样本的index,0到num_example-1,存成list
    # print(indices)
    # 随机读取数据
    random.shuffle(indices)  # 打乱indices，即打乱index,以做到随机访问每一个样本
    # print(indices)
    # 从0到num_examples-1,步长为batch_size
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size,num_examples)])
        # yield:以（x,y）的形式返回
        yield features[batch_indices],labels[batch_indices]

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

（4）定义损失函数

def squared_loss(y_hat, y):
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2

（5）定义优化算法

def sgd(params, lr, batch_size):
    """小批量随机梯度下降"""
    with torch.no_grad( ):
        for param in params:
            param -= lr * param.grad /batch_size
            param.grad.zero_()

（6）训练过程

lr = 0.03  #学习率
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X,y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)
        l.sum().backward()
        sgd([w,b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch+1},loss {float(train_l.mean()):f}')

epoch 1,loss 0.037877
epoch 2,loss 0.000149
epoch 3,loss 0.000053

2.线性回归简洁实现

（1）使用深度学习框架实现线性回归模型，生成数据集

import numpy as np
import torch
from torch.utils import data  # 处理数据的相关模块
from d2l import torch as d2l

true_w = torch.tensor([2,-3.4])
true_b = 4.2
# 通过人工数据生成的函数合成所需要的数据
features, labels = d2l.synthetic_data(true_w, true_b, 100)

（2）调用框架中现有的API来读取数据

def load_array(data_arrays, batch_size, is_train=True):
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset,batch_size,shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

[tensor([[-2.6414, -0.0434],
         [-0.4269, -0.6939],
         [-1.0043,  1.0792],
         [-0.7633,  0.5864],
         [-1.0033, -0.0062],
         [ 0.2628, -0.9052],
         [-1.2950, -0.1154],
         [ 1.1647, -1.1407],
         [ 1.4055, -1.1912],
         [ 0.4733,  1.5539]]),
 tensor([[-0.9327],
         [ 5.7303],
         [-1.4759],
         [ 0.6839],
         [ 2.2185],
         [ 7.8047],
         [ 2.0032],
         [10.4156],
         [11.0725],
         [-0.1272]])]

（3）使用框架预定义好的层

from torch import nn

net = nn.Sequential(nn.Linear(2,1))  # 输入维度为2，输出维度为1

（4）初始化模型参数

net[0].weight.data.normal_(0, 0.01) #使用正态分布替换data的值
net[0].bias.data.fill_(0)

tensor([0.])

（5）计算均方误差使用MSELoss类

Loss = nn.MSELoss()

（6）实例化SGD

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

（7）训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = Loss(net(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = Loss(net(features), labels)
    print(f'epoch {epoch+1}, loss {l:f}')

epoch 1, loss 0.000105
epoch 2, loss 0.000105
epoch 3, loss 0.000105

【相关方法】