【机器学习】033

【机器学习】033_反向传播

news2024/11/20 4:33:20

一、计算图、反向传播原理

1. 回顾前向传播

例：假设现在有一个神经网络，其仅有一个输出层和一个神经单元

· 定义 $z = wx+b$

· 定义 $a = g(z) = z = wx+b$ ，即激活函数对激活值不再做具体处理

· 定义平方损失函数 $J(w,b) = \frac{1}{2}(a-y)^2$ ，计算a的值与真实值的差距

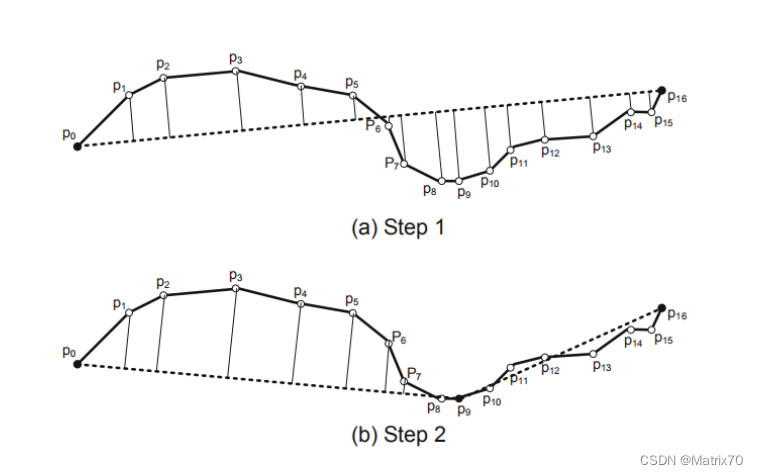
此时，通过计算图，我们可以看到前向传播的过程：

①输入 $x$ ，分别与权重 $w$ 和 $b$ 做运算得到 $z$ ，再经过激活函数得到 $a$ 的值；

②拿 $a$ 的值与真实值 $y$ 做比较，从而得到损失函数的值。

在这个过程中，我们通过计算图将得到损失函数 $J(w,b)$ 的每一小步操作都呈现了出来，并用诸如 $c$ 和 $d$ 的变量名表示其中的某一部分，※这方便我们后续进行反向传播的求导操作。

如果我们要实现梯度下降不断更新权重 $w$ 和 $b$ 的值从而减小损失函数，就需要知道损失函数对于 $w$ 和 $b$ 的导数值。这个过程我们称之为【反向传播】。

2. 反向传播

损失函数对于 $w$ 和 $b$ 的导数值不能够直接求导呈现，由于 $J(w,b)$ 是 $w$ 和 $b$ 经过了多个变换最终计算出来的，因此要对 $J(w,b)$ 求 $w$ 和 $b$ 的导数，就应该使用链式法则来进行计算。

如图所示，在计算图中进行反向传播的运算，最终可以通过链式法则得到 $\frac{\partial J}{\partial w}$ 和 $\frac{\partial J}{\partial b}$ 的值。

· 利用这些值，我们就可以进一步执行梯度下降算法的相关操作，来不断更新 $w$ 和 $b$ 的值从而使 $J(w,b)$ 最小。

· 一般地，当导数为0时，证明达到了极小值点，此时即是梯度下降收敛的位置。

※有关梯度下降算法的相关知识，详见先前学习笔记※

激活函数的选择：

目前使用较多的是ReLU函数，它的求导表现是要么让某个参数通过，要么让某个参数消失，因此优化表现更好，且缓解了梯度消失问题（后续会进一步学习）

二、使用 Sympy 的库和包自行计算导数

import sympy
# 使用J和w作为求导计算的符号
J, w = sympy.symbols('J, w')
# 确定两者之间的函数表达式
J = w**2
# diff()函数表示求第一个数对第二个数的导数
dJ_dw = sympy.diff(J, w)
print(dJ_dw)
print(dJ_dw.subs([(w,2)]))  # subs表示将w的值实际代入进去求dJ_dw的值

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1232998.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！