整合为学习笔记!参考阅读了几位大佬的作品,已标注出处~
机器学习的数学基础
-
线性与非线性变换

从几何意义上,线性变换表示的是直线的特性,符合两个性质: 变换前后零点不变,变换前后直线还是直线。
线性变换意味着可以将空间中的向量围绕零点进行旋转伸缩,但不能将其弯曲,否则,则是非线性变化。
非线性变换将空间进行了扭曲,比如把SVM中的核函数看做描述低维空间到高维空间的映射,把原始低维空间中线性不可分的数据变成高维空间中线性可分的数据,优雅解决了问题
从数值意义上,变换即函数,线性变换就是一阶导数为常数的函数,警如y=kx,把y=kx拓展为n维空间的映射,x、y看做n维向量,当k为常数时,易得满足同质性f(ka)=kf(a),当k为一个矩阵时易得满足可加性f(a+b)=f(a)+f(b)。
同质性和可加性又称为线性条件,满足该条件则为线性变换,反之则为非线性变换.
转载自:什么是线性变换和非线性变换? - 知乎
-
概率学基础
参阅: 机器学习中的概率模型 - 知乎
转载自:机器学习理论篇1:机器学习的数学基础 - 知乎
为什么使用概率?
概率论是用于表示不确定性陈述的数学框架,即它是对事物不确定性的度量。
在人工智能领域,我们主要以两种方式来使用概率论。首先,概率法则告诉我们AI系统应该如何推理,所以我们设计一些算法来计算或者近似由概率论导出的表达式。其次,我们可以用概率和统计从理论上分析我们提出的AI系统的行为。
计算机科学的许多分支处理的对象都是完全确定的实体,但机器学习却大量使用概率论。实际上如果你了解机器学习的工作原理你就会觉得这个很正常。因为机器学习大部分时候处理的都是不确定量或随机量。
随机变量
概率分布
给定某随机变量的取值范围,概率分布就是导致该随机事件出现的可能性。
从机器学习的角度来看,概率分布就是符合随机变量取值范围的某个对象属于某个类别或服从某种趋势的可能性。
条件概率
贝叶斯公式
先看看什么是“先验概率”和“后验概率”,以一个例子来说明:
假设某种病在人群中的发病率是0.001,即1000人中大概会有1个人得病,则有: P(患病) = 0.1%;即:在没有做检验之前,我们预计的患病率为P(患病)=0.1%,这个就叫作"先验概率"。
再假设现在有一种该病的检测方法,其检测的准确率为95%;即:如果真的得了这种病,该检测法有95%的概率会检测出阳性,但也有5%的概率检测出阴性;或者反过来说,但如果没有得病,采用该方法有95%的概率检测出阴性,但也有5%的概率检测为阳性。用概率条件概率表示即为:P(显示阳性|患病)=95%
现在我们想知道的是:在做完检测显示为阳性后,某人的患病率P(患病|显示阳性),这个其实就称为"后验概率"。
而这个叫贝叶斯的人其实就是为我们提供了一种可以利用先验概率计算后验概率的方法,我们将其称为“贝叶斯公式”。
期望
方差
协方差
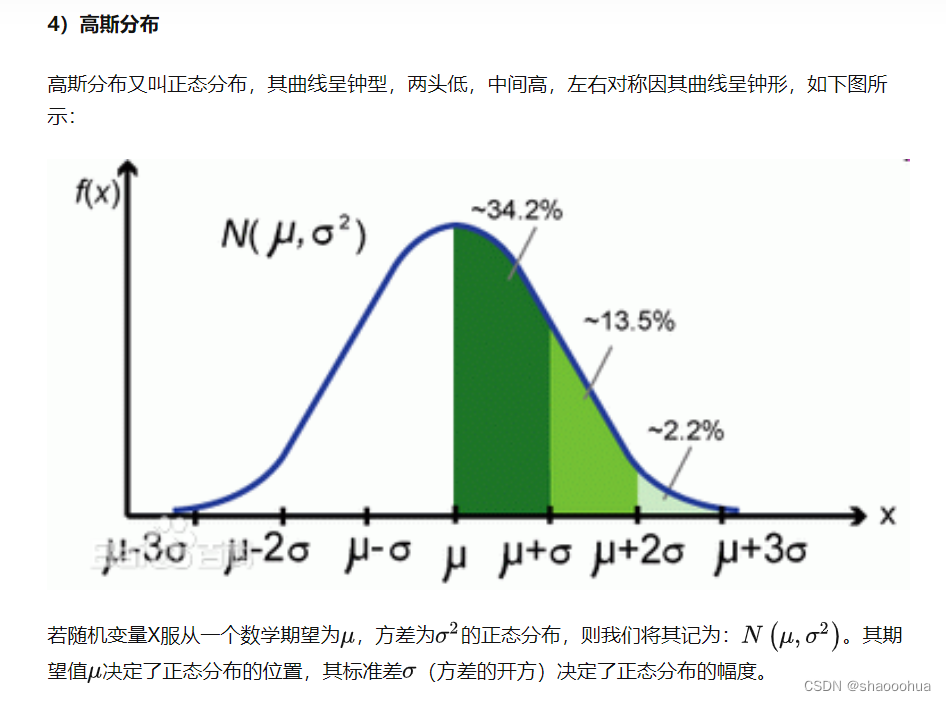
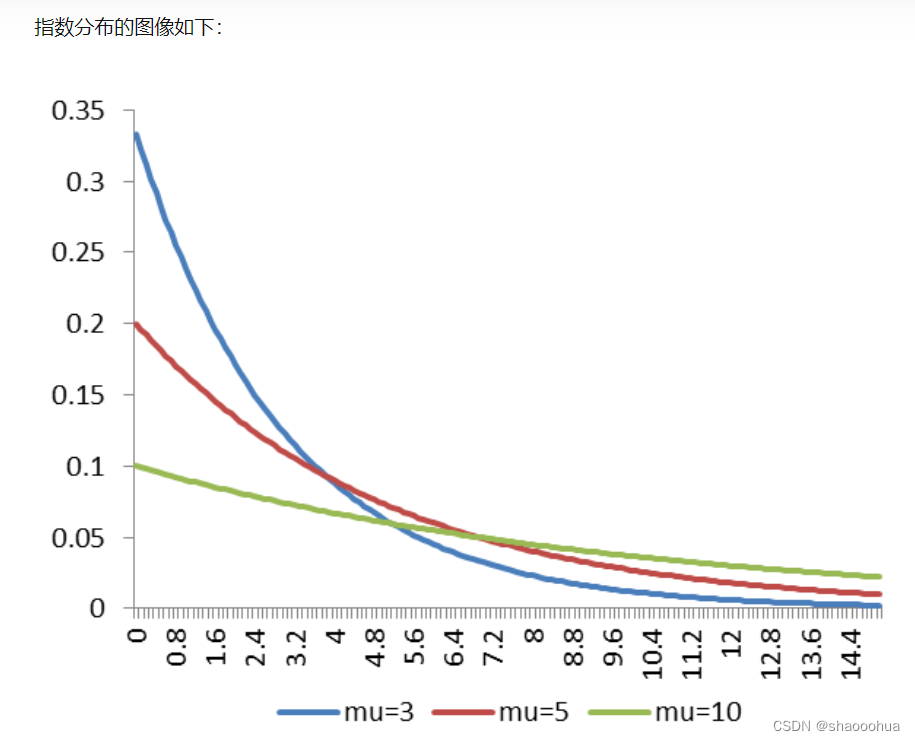
常见分布函数
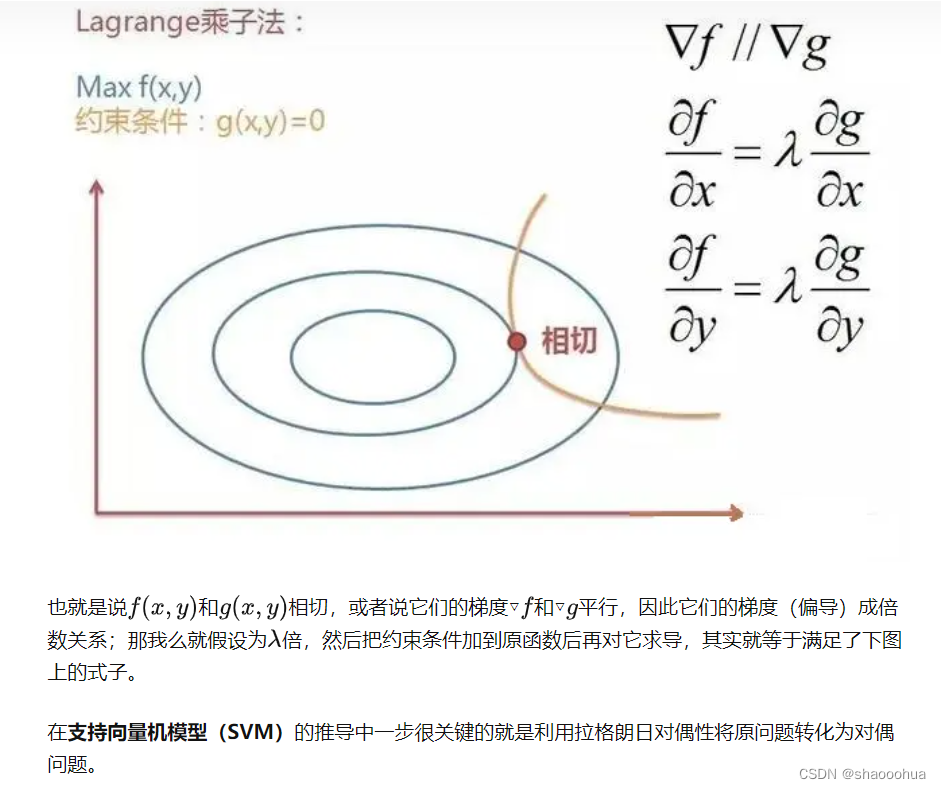
Lagrange乘子法
最大似然估计
-
熵
(联合熵、条件熵、相对熵、互信息、最大熵模型)


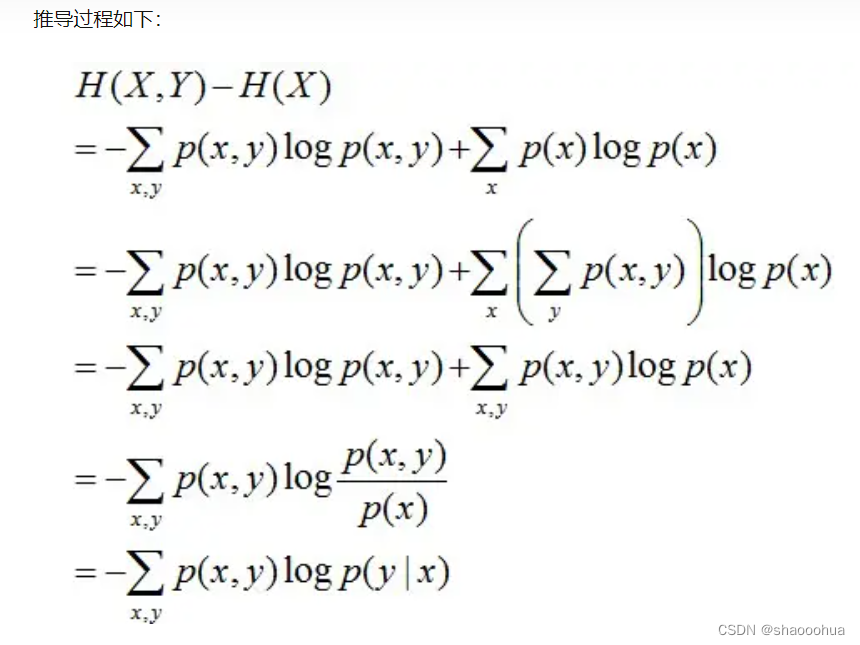





-
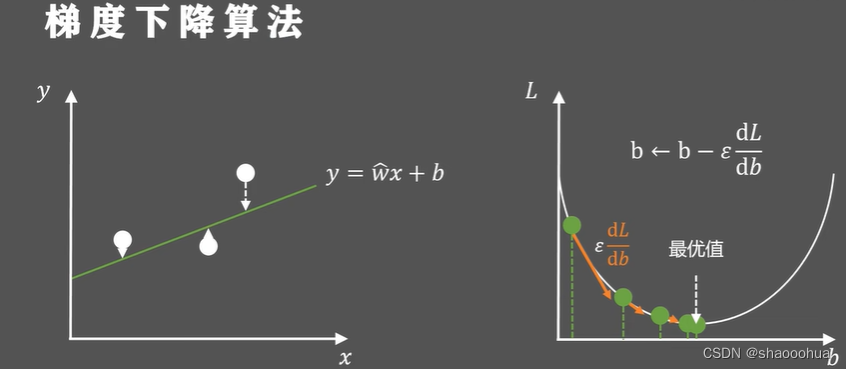
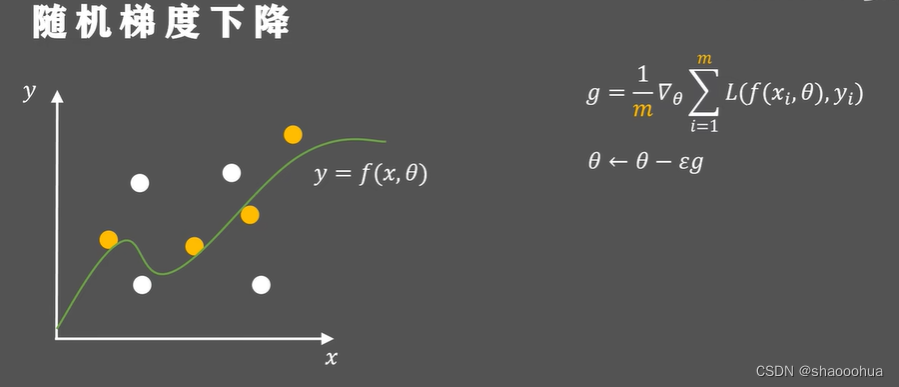
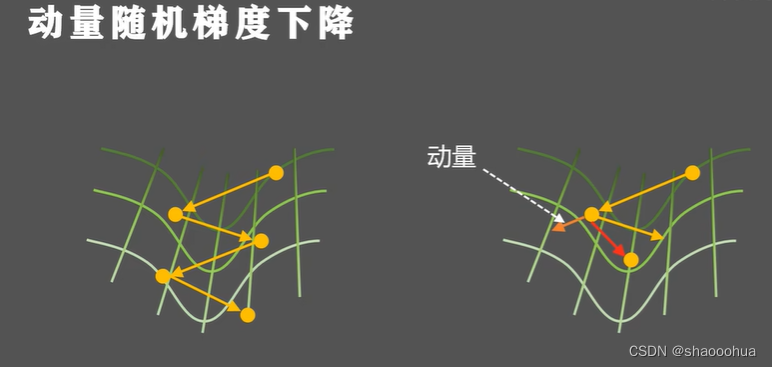
梯度下降法



















![浙大恩特客户资源管理系统fileupload.jsp,machord_doc.jsp接口任意文件上传漏洞复现 [附POC]](https://img-blog.csdnimg.cn/e1347f37dc734cb2b78e96b09eccf2aa.png)